Primzahlenlücke

Eine Primzahllücke ist die Differenz zwischen zwei aufeinanderfolgenden Primzahlen. Die kleinste Primzahllücke ist 3 - 2 = 1. Alle anderen Primzahllücken sind gerade, da 2 die einzige gerade Primzahl ist und somit die Differenz aus zwei ungeraden Zahlen gebildet wird. Zum Beispiel: 13 − 11 oder 23 − 19.

Bemerkung: Einige Autoren bezeichnen mit Primzahllücke abweichend hiervon die Anzahl zusammengesetzter Zahlen zwischen zwei Primzahlen, d. h. eins weniger als nach der hier verwendeten Definition.

Auftreten von Primzahllücken

• Da eine Lücke der Länge 1 nur zwischen einer geraden und einer ungeraden Primzahl auftreten kann, ist offensichtlich, dass es sie nur einmal gibt. (2 ist die einzige gerade Primzahl).
• Ob es unendlich viele Primzahlzwillinge, d. h. Lücken der Länge 2 gibt, ist eines der großen ungelösten Probleme der Mathematik.
• Abgesehen von 1 ist die Länge einer Primzahllücke immer gerade. Bei Primzahllücken gerader Länge müssen beide begrenzenden Zahlen ungerade sein.

Konstruktion beliebig großer Primzahllücken

Zu einer beliebigen natürlichen Zahl n ist es sehr leicht, die Existenz einer Primzahllücke mindestens der Länge n nachzuweisen. Sei nämlich N eine natürliche Zahl, die zu keiner der Zahlen 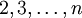$2, 3, \ldots, n$ teilerfremd ist. Dann sind auch die Zahlen 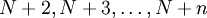$N+2, N+3, \ldots, N+n$ nicht teilerfremd zu N und folglich keine Primzahlen. Die größte Primzahl vor dieser Folge ist also höchstens gleich N + 1, die kleinste danach hingegen mindestens N + n + 1, so dass die Länge dieser Primzahllücke mindestens n ist.

Man hat hierbei verschiedene Möglichkeiten, ein N mit der geforderten Eigenschaft zu bilden. Beweistechnisch am einfachsten wählt man die Fakultät, also N = n!, in welchem Falle dann die betrachteten N + k sogar jeweils durch k teilbar sind. Ebenso gut kann man das kleinste gemeinsame Vielfache der Zahlen von 2 bis n wählen, $N=\operatorname{kgV}(2,\ldots,n)$.

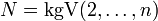Den kleinstmöglichen Kandidaten für N findet man durch die Primfakultät, 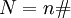$N=n\#$. Ist p die kleinste Primzahl größer als n, so gilt $n\# = (p-1)\#$, d.h. man hat sogar automatisch eine Lücke der Länge p − 1 gefunden.

Obwohl im letzten Fall N so klein wie möglich gewählt wurde, ist dennoch nicht garantiert, dass die gefundenen Lücken jeweils die erste Lücke der geforderten Länge sind. Insofern leisten alle diese Verfahren zwar gleichwertig den Nachweis, dass beliebig große Lücken existieren, sind aber bei einer Suche nach ersten Vorkommen großer Lücken nur bedingt von Nutzen.

Beispiel für n=6

Welche Lücken liefern die genannten Verfahren jeweils im Falle n = 6? Zum Vergleich: Die erste Lücke der Länge 6 tritt auf zwischen 23 und 29.

Fakultät

Es gilt 6!=720.

Da 720 durch 2 teilbar ist, ist es auch 720 + 2 = 722.

Da 720 durch 3 teilbar ist, ist es auch 720 + 3 = 723.

Da 720 durch 4 teilbar ist, ist es auch 720 + 4 = 724.

Da 720 durch 5 teilbar ist, ist es auch 720 + 5 = 725.

Da 720 durch 6 teilbar ist, ist es auch 720 + 6 = 726.

Man hat also eine Primzahllücke mindestens der Länge 6 zwischen den Primzahlkandidaten 721 und 727 gefunden. Da 721 durch 7 teilbar ist, ist die Lücke sogar noch größer. In der Tat wird sie eingerahmt von den Primzahlen 719 und 727 und hat folglich die Länge 8.

kgV (kleinstes gemeinsames Vielfaches)

Es gilt kgV(1,..,6) = 60.

Da 60 durch 2 teilbar ist, ist es auch 60 + 2 = 62.

Da 60 durch 3 teilbar ist, ist es auch 60 + 3 = 63.

Da 60 durch 4 teilbar ist, ist es auch 60 + 4 = 64.

Da 60 durch 5 teilbar ist, ist es auch 60 + 5 = 65.

Da 60 durch 6 teilbar ist, ist es auch 60 + 6 = 66.

Diesmal haben wir also eine Lücke der Länge mindestens 6 zwischen 61 und 67 gefunden. Beides sind „zufällig“ Primzahlen, d.h. die Länge der Lücke ist genau 6.

Primfakultät

Es ist $6\# = 2 \cdot 3 \cdot5 = 30$.

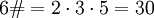Da 30 durch 2 teilbar ist, ist es auch 30 + 2 = 32.

Da 30 durch 3 teilbar ist, ist es auch 30 + 3 = 33.

Da 30 und 4 durch 2 teilbar sind, ist es auch 30 + 4 = 34.

Da 30 durch 5 teilbar ist, ist es auch 30 + 5 = 35.

Da 30 und 6 durch 2 teilbar sind, ist es auch 30 + 6 = 36.

Wiederum hat die gefundene Lücke genau die Länge 6, da 31 und 37 Primzahlen sind.

Wachstum der Funktionen

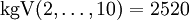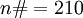Schon das ausgeführte Beispiel n = 6 zeigt, dass die Fakultät die bei weitem am raschesten wachsende unter den betrachteten Funktionen ist. Für n = 10 ist sich der Größenunterschied zwischen n! = 3628800, $\operatorname{kgV}(2,\ldots,10)=2520$ und $n\#=210$ noch deutlicher. Dagegen tritt bereits zwischen 113 und 127 eine Lücke der Länge 14 auf, so dass also selbst die Abschätzung durch 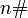$n\#$ weit davon entfernt ist, scharf zu sein.

Obere Schranken

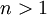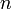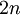Es gibt eine natürliche Begrenzung einer Primzahllücke, wie das Postulat von Joseph Bertrand zeigt: Für jedes $n > 1\$ gilt, zwischen $n\$ und $2n\$ liegt wenigstens eine Primzahl. Daraus folgt, das eine Primzahllücke, begonnen bei 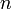$n\$ nicht größer sein kann als 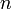$n\$ selbst.

Aus dem Primzahlsatz folgt, dass die Lücken für große n klein gegen n werden. Genauer lässt sich zeigen, dass es eine Konstante C gibt, so dass die Lücke nach der Primzahl p kleiner als 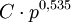$C \cdot p^{0{,}535}$ ist.^[1]

Das erste Auftreten einer Lücke einer bestimmten Größe

Eine Formel, die für ein n das erste Auftreten einer Primzahllücke der Länge n einigermaßen genau angibt, ist noch nicht bekannt.

Weblinks

• Prime Gaps -- from MathWorld (englisch)
• The Top-20 Prime Gaps (englisch)
• The Gaps Between Primes (englisch)

Einzelnachweise

1. ↑ R. C. Baker and G. Harman, "The difference between consecutive primes," Proc. Lond. Math. Soc., series 3, 72 (1996) 261-280.