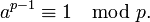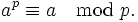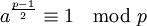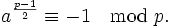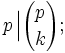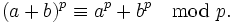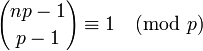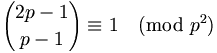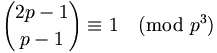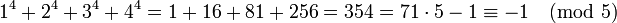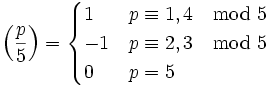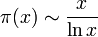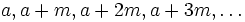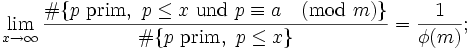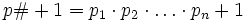Primzahlen

Eine Primzahl ist eine natürliche Zahl mit genau zwei natürlichen Zahlen als Teiler, nämlich der Zahl 1 und sich selbst. Die kleinsten Primzahlen sind

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 … (Folge A000040 in OEIS)

Das Wort „Primzahl“ kommt aus dem Französischen (nombre premier) und bedeutet „die erste Zahl“. Die fundamentale Bedeutung der Primzahlen für viele Bereiche der Mathematik beruht auf den folgenden drei Konsequenzen aus dieser Definition:

• Primzahlen lassen sich nicht als Produkt zweier natürlicher Zahlen, die beide größer als 1 sind, darstellen. Diese Eigenschaft wird als Definition für Verallgemeinerungen genutzt.
• Lemma von Euklid: Ist ein Produkt zweier natürlicher Zahlen durch eine Primzahl teilbar, so ist bereits einer der Faktoren durch sie teilbar.
• Existenz und Eindeutigkeit der Primfaktorzerlegung: Jede natürliche Zahl lässt sich als Produkt von Primzahlen schreiben. Diese Produktdarstellung ist bis auf die Reihenfolge der Faktoren eindeutig.

Eine natürliche Zahl größer als 1 heißt prim, wenn sie eine Primzahl ist, andernfalls heißt sie zusammengesetzt. Die Zahlen 0 und 1 sind weder prim noch zusammengesetzt.

Bereits die antiken Griechen interessierten sich für die Primzahlen und entdeckten einige ihrer Eigenschaften. Obwohl sie über die Jahrhunderte stets einen großen Reiz auf die Menschen ausübten, sind bis heute viele die Primzahlen betreffenden Fragen ungeklärt.

Über zweitausend Jahre lang konnte man keinen praktischen Nutzen aus dem Wissen über die Primzahlen ziehen. Dies änderte sich erst mit dem Aufkommen elektronischer Rechenmaschinen, bei denen die Primzahlen beispielsweise in der Kryptographie eine zentrale Rolle spielen.

Primfaktorzerlegung

→ Hauptartikel: Primfaktorzerlegung

Es gilt der Fundamentalsatz der Arithmetik: Jede positive ganze Zahl lässt sich bis auf die Reihenfolge eindeutig als Produkt von Primzahlen darstellen. Die in dieser Darstellung auftretenden Primzahlen nennt man die Primfaktoren der Zahl. Die Schwierigkeiten bei der Primfaktorzerlegung bezeichnet man als Faktorisierungsprobleme. Man versucht, sie mit geeigneten Faktorisierungsverfahren zu minimieren.

Aufgrund dieses Satzes, also dass sich jede natürliche Zahl durch Multiplikation von Primzahlen eindeutig darstellen lässt, nehmen die Primzahlen eine besondere atomare Stellung in der Mathematik ein. Alexander K. Dewdney bezeichnete diese als den Elementen der Chemie weitgehend ähnlich.

Praktische Anwendung

Aus der Primfaktorenzerlegung lässt sich erkennen, ob eine Zahl durch eine andere teilbar ist. Das kleinste gemeinsame Vielfache kgV und der größte gemeinsame Teiler ggT können leicht aus der Primfaktorenzerlegung bestimmt werden. In der Bruchrechnung können Brüche durch den ggT von Zähler und Nenner gekürzt werden, und zwei Brüche können auf den kleinsten gemeinsamen Nenner erweitert werden, um leichter addieren oder subtrahieren zu können.

Kryptographie

Eine wichtige Rolle spielen Primzahlen in der Kryptographie. Verschlüsselungssysteme wie RSA basieren darauf, dass kein effizientes Faktorisierungsverfahren bekannt ist. So ist es innerhalb von Sekunden problemlos möglich, zwei 500-stellige Primzahlen zu finden und miteinander zu multiplizieren. Mit den heutigen Methoden würde die Rückgewinnung der beiden Primfaktoren aus diesem 999-stelligen oder 1000-stelligen Produkt dagegen sehr lange Zeit dauern. Primzahlen werden auch bei der Programmierung von Hashtabellen verwendet.

Eigenschaften von Primzahlen

Mit Ausnahme der Zahl 2 sind alle Primzahlen p ungerade, denn alle größeren geraden Zahlen lassen sich außer durch sich selbst und 1 auch noch (mindestens) durch 2 teilen. Damit hat jede Primzahl außer 2 die Form 2k + 1 mit einer natürlichen Zahl k.

Jede Primzahl mit Ausnahme der 2 lässt sich einer der beiden Klassen „Primzahl der Form 4k + 1“ oder „Primzahl der Form 4k + 3“ zuordnen, wobei k eine natürliche Zahl ist. Darüber hinaus hat jede Primzahl p > 3 die Form p = 6k + 1 oder p = 6k − 1, wobei k eine natürliche Zahl ist. Nach dem dirichletschen Primzahlsatz gibt es in jeder dieser vier Klassen unendlich viele Primzahlen.

Jede natürliche Zahl der Form 4m + 3 mit einer nichtnegativen ganzen Zahl m enthält mindestens einen Primfaktor der Form 4k + 3. Eine entsprechende Aussage über Zahlen der Form 4m + 1 oder Primfaktoren der Form 4k + 1 ist nicht möglich.

Eine Primzahl p > 2 lässt sich genau dann in der Form a² + b² mit ganzen Zahlen a,b schreiben, wenn p die Form 4k + 1 hat. In diesem Fall ist die Darstellung im Wesentlichen eindeutig, d.h. bis auf Reihenfolge und Vorzeichen von a,b. Diese Darstellung entspricht der Primfaktorzerlegung

p = (a + bi)(a − bi)

im Ring der ganzen gaußschen Zahlen.

Die Zahl −1 ist ein quadratischer Rest modulo jeder Primzahl der Form 4k + 1 und quadratischer Nichtrest modulo jeder Primzahl der Form 4k + 3.

Der kleine Satz von Fermat

Es sei p eine Primzahl. Für jede ganze Zahl a, die nicht durch p teilbar ist, gilt (für die Notation siehe Kongruenz):

$a^{p-1} \equiv 1 \mod p.$

Eine äquivalente Formulierung lautet: Für jede ganze Zahl a gilt

$a^p\equiv a\mod p.$

Es gibt Zahlen, die keine Primzahlen sind, sich aber dennoch zu einem Teil der Basen a wie Primzahlen verhalten und somit den kleinen Satz von Fermat erfüllen. Solche Nichtprimzahlen nennt man fermatsche Pseudoprimzahlen. Pseudoprimzahlen, die pseudoprim zu allen Basen a sind, welche nicht Teiler dieser Pseudoprimzahlen sind, nennt man Carmichael-Zahlen.

Besonders in diesem Zusammenhang zeigt sich die Problematik von Pseudoprimzahlen: Sie werden von Algorithmen, die den kleinen Satz von Fermat nutzen, um festzustellen, ob eine bestimmte Zahl prim ist, fälschlicherweise für Primzahlen gehalten. Wenn allerdings ein Verschlüsselungsverfahren wie RSA eine zusammengesetzte Zahl statt einer Primzahl verwendet, ist die Verschlüsselung nicht mehr sicher. Deshalb müssen bei solchen Verfahren Primzahltests verwendet werden, die mit einer sehr hohen Wahrscheinlichkeit Primzahlen von zusammengesetzten Zahlen unterscheiden können. Diese Wahrscheinlichkeit ist bei Verwendung des kleinen Satzes von Fermat als Basis allein nicht hoch genug, es gibt aber sicherere Primzahltests.

Euler und das Legendre-Symbol

Eine einfache Folge aus dem kleinen Satz von Fermat ist die folgende Aussage: Für jede ungerade Primzahl p und jede ganze Zahl a, die nicht durch p teilbar ist, gilt entweder

$a^{\frac{p-1}{2}} \equiv 1 \mod p$

oder

$a^{\frac{p-1}{2}} \equiv -1 \mod p.$

Man kann zeigen, dass der erste Fall genau dann eintritt, wenn es eine Quadratzahl m² gibt, die kongruent zu a modulo p ist, siehe Legendre-Symbol.

Binomialkoeffizient

Für Primzahlen p und 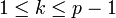$1\leq k\leq p-1$ gilt

$p\,\Big|{p\choose k};$

zusammen mit dem binomischen Satz folgt daraus

$(a+b)^p\equiv a^p+b^p\mod p.$

Für ganze Zahlen a,b folgt diese Aussage auch direkt aus dem kleinen fermatschen Satz, aber sie ist beispielsweise auch für Polynome mit ganzzahligen Koeffizienten anwendbar; im allgemeinen Kontext entspricht sie der Tatsache, dass die Abbildung 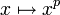$x\mapsto x^p$ in Ringen der Charakteristik p ein Homomorphismus ist, der so genannte Frobenius-Homomorphismus.

Aus dem Satz von Wilson (p ist genau dann eine Primzahl, wenn 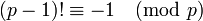$(p-1)! \equiv -1 \pmod p$ ist) folgt, dass für jede Primzahl p und jede natürliche Zahl n die Kongruenz

${{np-1}\choose{p-1}} \equiv 1 \pmod{p}$

erfüllt ist.

Charles Babbage bewies 1819, dass für jede Primzahl p > 2 diese Kongruenz gilt:

${{2p-1}\choose{p-1}} \equiv 1 \pmod{p^2}$

Der Mathematiker Joseph Wolstenholme (1829–1891) bewies dann 1862, dass für jede Primzahl p > 3 die folgende Kongruenz gilt:

${{2p-1}\choose{p-1}} \equiv 1 \pmod{p^3}$

Giuga

Aus dem kleinen Satz von Fermat folgt, dass für eine Primzahl p gilt:

$1^{p-1} + 2^{p-1} + ... + (p-1)^{p-1} \equiv -1 \pmod{p}$

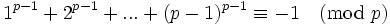
Beispiel p = 5:

$1^4 + 2^4 + 3^4 + 4^4 = 1 + 16 + 81 + 256 = 354 = 71\cdot 5 - 1\equiv -1 \pmod{5}$

Giuseppe Giuga vermutete, dass auch die umgekehrte Schlussrichtung gilt, dass also eine Zahl mit dieser Eigenschaft stets prim ist. Es ist nicht geklärt, ob diese Vermutung richtig ist. Bekannt ist aber, dass ein Gegenbeispiel mehr als 10.000 Dezimalstellen haben müsste. Im Zusammenhang mit Giugas Vermutung werden die Giuga-Zahlen untersucht.

Lineare Rekursionen

Den kleinen fermatschen Satz kann man auch in der Form lesen: In der Folge aⁿ − a ist das p-te Folgenglied für eine Primzahl p stets durch p teilbar. Ähnliche Eigenschaften besitzen auch andere Folgen von exponentiellem Charakter, wie die Lucas-Folge (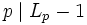$p\mid L_p-1$) und die Perrin-Folge (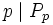$p\mid P_p$). Für andere lineare Rekursionen gelten analoge, aber kompliziertere Aussagen, beispielsweise für die Fibonacci-Folge 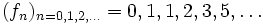$(f_n)_{n=0,1,2,\ldots}=0,1,1,2,3,5,\ldots$: Ist p eine Primzahl, so ist 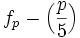$f_p-\Big(\frac p5\Big)$ durch p teilbar; dabei ist

$\Big(\frac p5\Big)=\begin{cases}1&p\equiv 1,4\mod 5\\-1&p\equiv2,3\mod 5\\0&p=5\end{cases}$

das Legendre-Symbol.

Divergenz der Summe der Kehrwerte

Die Folge der Summe der Kehrwerte der Primzahlen bis hin zu einer bestimmten Primzahl p_n (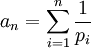$a_n=\sum_{i=1}^{n} \frac{1}{p_i}$) hat keinen Grenzwert. Das bedeutet, für ein genügend großes n lässt sich jede erdenkliche reelle Zahl übertreffen. Dies ist zunächst einmal verblüffend, da die Primzahllücken im Schnitt immer weiter zunehmen.

Weiteres

Zwei natürliche Zahlen, deren Summe eine Primzahl ergibt, sind immer teilerfremd. Umgekehrt zeigt jedoch das einfache Gegenbeispiel 3 + 5 = 8, dass die Summe zweier teilerfremder Zahlen nicht zwingend eine Primzahl ergibt.

Primzahltests

→ Hauptartikel: Primzahltest

Ob eine Zahl eine Primzahl ist, kann man mit einem Primzahltest entscheiden. Es gibt mehrere solcher Verfahren, deren Grundlagen meist besondere Eigenschaften von Primzahlen sind. In der Praxis wird der Miller-Rabin-Test am häufigsten verwendet, der eine extrem kurze Laufzeit hat, allerdings mit kleiner Wahrscheinlichkeit falsch-positive Ergebnisse liefert. Mit dem AKS-Primzahltest ist es möglich, Zahlen in polynomialer Laufzeit zu testen. Allerdings ist er in der Praxis deutlich langsamer als der Miller-Rabin-Test.

Größte bekannte Primzahl

Der Grieche Euklid hat im vierten Jahrhundert vor Christus logisch geschlussfolgert, dass es unendlich viele Primzahlen gibt; diese Aussage wird als Satz von Euklid bezeichnet. Euklid führte einen Widerspruchsbeweis für die Richtigkeit dieses Satzes: Ausgehend von der Annahme, dass es nur endlich viele Primzahlen gibt, lässt sich eine weitere Primzahl konstruieren, was einen Widerspruch zur Annahme darstellt. Somit kann eine endliche Menge niemals alle Primzahlen enthalten, also gibt es unendlich viele. Heute kennt man eine ganze Reihe von Beweisen für den Satz von Euklid, siehe Beweisarchiv.

Der Satz von Euklid besagt, dass es keine größte Primzahl gibt. Es ist jedoch kein Verfahren bekannt, das effizient beliebig große Primzahlen generiert, so dass es stets eine größte bekannte Primzahl gab, seitdem sich die Menschen mit Primzahlen befassen. Derzeit ist es 2^43.112.609 − 1, eine Zahl mit 12.978.189 (dezimalen) Stellen, die am 23. August 2008 auf einem Computer der mathematischen Fakultät an der University of California, Los Angeles, gefunden wurde. Der Verantwortliche für die Computer der Fakultät, Edson Smith, hatte das Programm des GIMPS-Projekts als Bildschirmschoner auf den Rechnern der Fakultät eingerichtet. Die Entdeckung dieser Primzahl qualifiziert sich mit mehr als 10 Millionen Dezimalstellen für den von der Electronic Frontier Foundation ausgeschriebenen Preis von 100.000 US-Dollar.

Die größte bekannte Primzahl war fast immer eine Mersenne-Primzahl, also von der Form 2ⁿ − 1, da in diesem Spezialfall der Lucas-Lehmer-Test angewendet werden kann, ein im Vergleich zur allgemeinen Situation sehr schneller Primzahltest. Bei der Suche nach großen Primzahlen werden deshalb nur Zahlen dieses oder eines ähnlich geeigneten Typs auf Primalität untersucht.

Liste der Rekordprimzahlen nach Jahren

Zahl	Ziffernanzahl (im Dezimalsystem)	Jahr	Entdecker (genutzter Computer)
217 - 1	6	1588	Cataldi
219 - 1	6	1588	Cataldi
231 - 1	10	1772	Euler
(259 - 1)/179951	13	1867	Landry
2127 - 1	39	1876	Lucas
(2148+1)/17	44	1951	Ferrier
180·(2127-1)2+1	79	1951	Miller & Wheeler (EDSAC1)
2521-1	157	1952	Robinson (SWAC)
2607-1	183	1952	Robinson (SWAC)
21279-1	386	1952	Robinson (SWAC)
22203-1	664	1952	Robinson (SWAC)
22281-1	687	1952	Robinson (SWAC)
23217-1	969	1957	Riesel (BESK)
24423-1	1332	1961	Hurwitz (IBM7090)
29689-1	2917	1963	Gillies (ILLIAC 2)
29941-1	2993	1963	Gillies (ILLIAC 2)
211213-1	3376	1963	Gillies (ILLIAC 2)
219937-1	6002	1971	Tuckerman (IBM360/91)
221701-1	6533	1978	Noll & Nickel (CDC Cyber 174)
223209-1	6987	1979	Noll (CDC Cyber 174)
244497-1	13395	1979	Nelson & Slowinski (Cray 1)
286243-1	25962	1982	Slowinski (Cray 1)
2132049-1	39751	1983	Slowinski (Cray X-MP)
2216091-1	65050	1985	Slowinski (Cray X-MP/24)
2216193-1	65087	1989	„Amdahler Sechs“ (Amdahl 1200)
2756839-1	227832	1992	Slowinski & Gage (Cray 2)
2859433-1	258716	1994	Slowinski & Gage (Cray C90)
21257787-1	378632	1996	Slowinski & Gage (Cray T94)
21398269-1	420921	1996	Armengaud, Woltman (GIMPS, Pentium 90 MHz)
22976221-1	895932	1997	Spence, Woltman (GIMPS, Pentium 100 MHz)
23021377-1	909526	1998	Clarkson, Woltman, Kurowski (GIMPS, Pentium 200 MHz)
26972593-1	2098960	1999	Hajratwala, Woltman, Kurowski (GIMPS, Pentium 350 MHz)
213466917-1	4053946	2001	Cameron, Woltman, Kurowski (GIMPS, Athlon 800 MHz)
220996011-1	6320430	2003	Shafer (GIMPS, Pentium 4 2 GHz)
224036583-1	7235733	2004	Findley (GIMPS, Pentium 4 2,4 GHz)
225964951-1	7816230	2005	Nowak (GIMPS, Pentium 4 2,4 GHz)
230402457-1	9152052	2005	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
232582657-1	9808358	2006	Cooper, Boone (GIMPS)
237156667-1	11185272	2008	Hans- Michael Elvenich, Woltman, Kurowski, et al (GIMPS)
243112609-1	12978189	2008	Smith, Woltman, Kurowski, et al (GIMPS)
6328548*26328548+1		2009	Dennis R. Gesker (Intel Xeon E5420 @ 2.50GHz)

Verteilung der Primzahlen

Zur Untersuchung der Verteilung der Primzahlen betrachtet man unter anderem die Funktion

$\pi:\Bbb N\to \Bbb N,\;n\mapsto\pi(n)$,

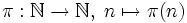die die Anzahl der Primzahlen 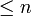$\leq n$ angibt. Zum Beispiel ist

$\pi(10) = 4\ ;\ \pi(100) = 25\ ;\ \pi(1000) = 168$.

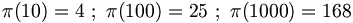Diese Funktion und ihr Wachstumsverhalten ist ein beliebter Forschungsgegenstand in der Zahlentheorie. Mit der Zeit wurden einige Näherungsformeln entwickelt und verbessert.

Der Primzahlsatz besagt, dass

$\pi(x) \sim \frac{x}{\ln x}$

gilt, d.h. dass der Quotient von linker und rechter Seite für 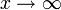$x\to\infty$ gegen 1 strebt.

Der dirichletsche Primzahlsatz dagegen schränkt die Betrachtung auf Restklassen ein: Es sei m eine natürliche Zahl. Ist a eine ganze Zahl, die zu m nicht teilerfremd ist, so kann die arithmetische Folge

$a,a+m,a+2m,a+3m,\ldots$

höchstens eine Primzahl enthalten, weil alle Folgenglieder durch den größten gemeinsamen Teiler von a und m teilbar sind. Ist a aber teilerfremd zu m, so besagt der dirichletsche Primzahlsatz, dass die Folge unendlich viele Primzahlen enthält. Beispielsweise gibt es unendlich viele Primzahlen der Form 4k + 1 und unendlich viele der Form 4k + 3 (k durchläuft jeweils die nichtnegativen natürlichen Zahlen).

Diese Aussage kann noch in der folgenden Form präzisiert werden: Es gilt

$\lim_{x\to\infty}\frac{\#\{p\ \mathrm{prim},\ p\leq x\ \mathrm{und}\ p\equiv a\pmod m\}}{\#\{p\ \mathrm{prim},\ p\leq x\}}=\frac1{\phi(m)};$

dabei ist φ(m) die eulersche φ-Funktion. In diesem Sinne liegen also für ein festes m in den Restklassen 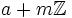$a+m\mathbb Z$ mit ggT(a,m) = 1 jeweils „gleich viele“ Primzahlen.

Siehe auch: Ulam-Spirale

Formeln zur Generierung von Primzahlen

Einer der ältesten Algorithmen zur Bestimmung von Primzahlen ist das Sieb des Eratosthenes, bei dem nacheinander aus einer Liste der natürlichen Zahlen >1 die Zahlen gestrichen werden, die Vielfache der jeweils kleinsten noch nicht gestrichenen Zahl sind. Dadurch bleiben die Primzahlen innerhalb der Ausgangsliste übrig.

Man kennt keine Formel, die eine effiziente, direkte Berechnung der n-ten Primzahl ermöglichen würde. Es gibt allerdings Formeln, bei denen eine gewisse Wahrscheinlichkeit besteht, dass die erzeugten Zahlen eine Primzahl sein könnten. Trotzdem müssen die erzeugten Zahlen auf ihre Eigenschaft als Primzahl getestet werden.

Schon Euler gab die Formeln n² + n + 17 und n² − n + 41 an, die für 0 < n < 16 bzw. 0 < n < 41 Primzahlen liefern. Auch für größere Werte von n liefern die beiden Formeln viele Primzahlen, weil das Ergebnis nie durch Primzahlen p < 17 bzw. p < 41 ganzzahlig teilbar ist. Allgemein gibt es viele solche Formeln an² + bn + c, wodurch sich die auffällige Ulam-Spirale erklärt.

Die beliebteste ist die der Mersenne-Zahl M_n = 2ⁿ − 1 bei der M_n eine Primzahl ist. Durch die besonderen Eigenschaften der Teiler von Mersenne-Zahlen eignen sie sich für die Suche nach möglichst großen Primzahlen.

Fermat vermutete, dass alle Zahlen der Form 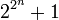$2^{2^n}+1$ prim sind; man nennt sie Fermat-Zahlen. Tatsächlich ist aber für n > 4 keine derartige Primzahl bekannt.

Auch bekannt ist eine Anwendung des Satzes von Euklid, bei der auf das Primorial eine 1 aufaddiert wird:

$p\# + 1 = p_1 \cdot p_2 \cdot \ldots \cdot p_n + 1$

Hierbei werden alle aufeinanderfolgenden Primzahlen von 2 bis p_n = p miteinander multipliziert.

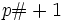$p\# + 1$ ist prim für p = 2, 3, 5, 7, 11, 31, 379, 1019, 1021, …

Weitere Formeln:

• n! − 1 ist prim für n = 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, … (Folge A002982 in OEIS)
• n! + 1 ist prim für n = 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154 …
• Primzahlen der Form kgV(1,…,n)+1 sind: 2, 3, 7, 13, 61, 421, 2521, 232792561, …

Spezielle Primzahlen und Primzahlkonstellationen

• Primzahlzwillinge
• Primzahldrillinge
• Primzahlvierlinge
• Primzahlsechslinge
• Wall-Sun-Sun-Primzahlen
• Cullen- und Woodall-Zahlen
• Cunningham-Ketten
• Prothsche Primzahlen
• glückliche Primzahlen
• Mersenne-Primzahlen
• Sophie-Germain-Primzahlen

Weitere spezielle Arten von Primzahlen finden sich in der Kategorie:Primzahl.

Warum ist die Zahl 1 keine Primzahl?

Die einfachste Antwort auf die Frage, warum die 1 keine Primzahl ist, folgt aus der Definition:

• Eine natürliche Zahl wird dann Primzahl genannt, wenn sie durch genau zwei natürliche Zahlen teilbar ist. Die Zahl 1 ist aber nur durch eine natürliche Zahl, nämlich die Zahl 1, teilbar. Deshalb ist sie per definitionem keine Primzahl.

Die folgenden Antworten gehen auf den Zweck dieser Definition ein:

• Damit man eine eindeutige Primfaktorzerlegung bekommt (man hätte sonst beliebig viele 1-Faktoren darin).
• Weil 1 eine Einheit ist (siehe den Artikel Primelement).
• Weil man ansonsten bei nahezu allen Aussagen über Primzahlen schreiben müsste: „Für alle Primzahlen mit Ausnahme der 1 gilt…“. Beispielsweise in der Theorie der endlichen Körper.

Siehe hierzu auch: Wikibooks: Warum 1 keine Primzahl ist

Primzahllücken

→ Hauptartikel: Primzahllücke

Die Differenz zwischen zwei benachbarten Primzahlen heißt Primzahllücke. Diese Differenz schwankt, und obwohl es unendlich viele Primzahlen gibt, lassen sich Primzahllücken mit einer frei wählbaren Mindestgröße finden.

Verallgemeinerung

In der Ringtheorie wird das Konzept der Primzahl auf die Elemente eines beliebigen kommutativen unitären Rings verallgemeinert. Die entsprechenden Begriffe sind Primelement und irreduzibles Element.

Die Primzahlen und deren Negative sind dann genau die Primelemente und auch genau die irreduziblen Elemente des Rings der ganzen Zahlen. In faktoriellen Ringen, das sind Ringe mit eindeutiger Primfaktorisierung, fallen die Begriffe Primelement und irreduzibles Element zusammen; im Allgemeinen ist die Menge der Primelemente jedoch nur eine Teilmenge der Menge der irreduziblen Elemente.

Insbesondere im zahlentheoretisch bedeutsamen Fall der Dedekindringe übernehmen Primideale die Rolle der Primzahlen.

Literatur

• Paulo Ribenboim: The New Book of Prime Number Records. 3. Auflage. Springer Verlag, New York 1996, ISBN 0-387-94457-5.
• Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. Verlag C.H.Beck, München 2004, ISBN 3-406-52320-X.
• Władysław Narkiewicz: The Development of Prime Number Theory. Springer-Verlag, Berlin 2000, ISBN 3-540-66289-8.
• Peter Bundschuh: Einführung in die Zahlentheorie. 5. Auflage. Springer Verlag, Berlin 2002, ISBN 3-540-43579-4.

Weblinks

• The Prime Pages
• Primzahlenseite primzahlen.de
• Vortragsreihe von Dr. Rudolf Taschner (TU Wien)