Projektiver Modul

Im mathematischen Gebiet der Kategorientheorie sind projektive Objekte eine Verallgemeinerung des Begriffs der Freiheit in der Algebra.

Ein Objekt P einer Kategorie C heißt projektiv, wenn für jeden Epimorphismus f: X → Y die induzierte Abbildung

Mor_C(P,X) → Mor_C(P,Y), $g\mapsto f\circ g$

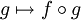
surjektiv ist.

Beispiele

• Projektive Gruppen sind genau die freien Gruppen.
• Projektive abelsche Gruppen sind genau die freien abelschen Gruppen. Achtung: freie abelsche Gruppen sind i.a. keine freien Gruppen.
• Allgemein sind alle freien Moduln über einem Ring projektiv.
• Gebrochene Ideale in einem Dedekindring sind projektiv, aber im Allgemeinen nicht frei.
• Ein endlich erzeugter Modul über einem noetherschen Ring ist genau dann projektiv, wenn die zugehörige Modulgarbe lokal frei ist.
• Ein endlich erzeugter Modul ist genau dann projektiv, wenn er direkter Summand eines freien Moduls ist.

Eigenschaften

Ist in der Kategorie C jedes Objekt Quotient eines projektiven Objektes, d.h. gibt es zu jedem Objekt 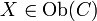$X\in \operatorname{Ob}(C)$ einen Epimorphismus 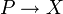$P\rightarrow X$, in dem P projektiv ist, so sagt man auch, C besitze genügend projektive Objekte. Diese Eigenschaft spielt eine Rolle im Zusammenhang mit abgeleiteten Funktoren. Beispielsweise besitzt die Kategorie der Gruppen genügend projektive Objekte, weil jede Gruppe Quotient einer freien Gruppe ist (Darstellung durch Erzeugende und Relationen).

Siehe auch

• Der duale Begriff ist der des injektiven Objektes.
• Die Isomorphieklassen endlich erzeugter projektiver Moduln werden durch die nullte algebraische K-Theorie beschrieben.