- Projektiver Raum
-
Der projektive Raum ist in der Mathematik ein grundlegender Begriff sowohl der Differentialgeometrie als auch der algebraischen Geometrie. Geometrisch kann man den projektiven Raum als Erweiterung des affinen Raumes auffassen. Bei dieser Erweiterung fügt man zu den Punkten des Raumes für jede Schar paralleler Geraden im affinen Raum jeweils ihre Richtung als neuen Punkt (Fernpunkt) hinzu. Damit entfallen in Sätzen und Beweisen viele Fallunterscheidungen, die in der affinen Formulierung aufgrund der Parallelität nötig sind. In der Koordinatendarstellung geschieht diese Erweiterung, indem im affinen Raum homogene Koordinaten eingeführt werden und die Einschränkung, dass die dabei zusätzlich eingeführte Koordinate nicht 0 sein darf, fallengelassen wird. So gelangt man zu einem projektiven Koordinatensystem des projektiven Raumes.
Für projektive Räume gilt ein Dualitätsprinzip.
Inhaltsverzeichnis
Definition
Auf
 sei die Äquivalenzrelation
sei die Äquivalenzrelationdefiniert. In Worten heißt dies, x ist äquivalent zu y genau dann, wenn es ein
 gibt, so dass x = λy gilt. Alle Punkte auf einer Geraden durch den Ursprung, der Ursprung ist nicht enthalten, werden also miteinander identifiziert und nicht mehr unterschieden. Der Quotientenraum
gibt, so dass x = λy gilt. Alle Punkte auf einer Geraden durch den Ursprung, der Ursprung ist nicht enthalten, werden also miteinander identifiziert und nicht mehr unterschieden. Der Quotientenraum  wird reeller, n-dimensionaler projektiver Raum genannt und mit
wird reeller, n-dimensionaler projektiver Raum genannt und mit  notiert.
notiert.Im Fall n=1 spricht man von der projektiven Gerade (auch: projektive Linie) und im Fall n=2 von einer projektiven Ebene. Wählt man statt
 den komplexen Vektorraum
den komplexen Vektorraum  so erhält man mit der analogen Definition mit
so erhält man mit der analogen Definition mit  den komplex projektiven Raum der (komplexen) Dimenson n. Die Koordinaten des Projektiven Raums, welche ja Äquivalenzklassen sind, werden durch
den komplex projektiven Raum der (komplexen) Dimenson n. Die Koordinaten des Projektiven Raums, welche ja Äquivalenzklassen sind, werden durch ![[x_0 : \ldots : x_n] \in \R P^n](a/cfa7ea789f39734f3f510cbe5f210150.png) notiert und heißen homogene Koordinaten.
notiert und heißen homogene Koordinaten.Allgemeiner können auch projektive Räume über beliebigen anderen Körpern (an Stelle von
 bzw.
bzw.  ) konstruiert werden.
) konstruiert werden.Ein allgemeinerer Begriff des projektiven Raumes wird in der synthetischen Geometrie verwendet, vor allem für den Fall n = 2 die projektive Ebene. Die Axiomatik dieses allgemeineren Begriffes wird im Hauptartikel Projektive Geometrie dargestellt.
Beispiel: Riemann'sche Zahlenkugel
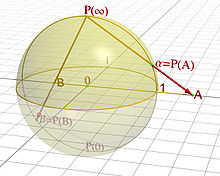 Stereographische Rückprojektionen der komplexen Zahlen A und B auf die Punkte α und β der Riemann'schen Zahlenkugel
Stereographische Rückprojektionen der komplexen Zahlen A und B auf die Punkte α und β der Riemann'schen Zahlenkugel
Die komplex-projektive Gerade ist nach obiger Definition gerade die Menge der komplexen Geraden in
 , welche durch den Ursprung
, welche durch den Ursprung  gehen.
gehen.Die komplex-projektive Gerade kann man auch als die reell-zweidimensionale Sphäre beziehungsweise Riemann'sche Zahlenkugel
auffassen. Die Übereinstimmung mit obigen Begriffen ergibt sich wie folgt: Bezeichne mit
 den "Nordpol". Betrachte die stereographische Projektion
den "Nordpol". Betrachte die stereographische Projektionwelche durch
 gegeben ist. Anschaulich legt man durch (x,y,z) und den Nordpol eine (reelle) Gerade und wählt den Schnittpunkt dieser Geraden mit der Ebene als Bildpunkt der Abbildung. Die Korrespondenz zwischen S2 und
gegeben ist. Anschaulich legt man durch (x,y,z) und den Nordpol eine (reelle) Gerade und wählt den Schnittpunkt dieser Geraden mit der Ebene als Bildpunkt der Abbildung. Die Korrespondenz zwischen S2 und  ist nun durch
ist nun durch  ,
,  gegeben.
gegeben.Eigenschaften
- Die reellen und komplexen projektiven Räume sind kompakte Mannigfaltigkeiten. Die oben erwähnten Abbildungen sind Abbildungen von Mannigfaltigkeiten.
- Der projektive Raum ist ein Beispiel für eine nicht affine algebraische Varietät bzw. ein nicht affines Schema. Im algebraisch-geometrischen Kontext kann man anstelle der reellen oder komplexen Zahlen jeden beliebigen Körper oder Ring einsetzen.
- Untermannigfaltigkeiten bzw. -varietäten des projektiven Raums werden als projektive Mannigfaltigkeiten bzw. projektive Varietäten bezeichnet.
Projektive Teilräume und abgeleitete Räume
In diesem Abschnitt wird im Sinne der obigen allgemeineren Definition von einem n − dimensionalen projektiven Raum KPn über einem beliebigen Körper K ausgegangen, die Punkte des Raumes können also als eindimensionale Unterräume von Kn + 1 angesehen werden.
- Jedem k + 1-dimensionalen Unterraum
 von Kn + 1 ist ein k-dimensionaler projektiver Teilraum Sk von KPn zugeordnet. Man nennt Sk auch eine (verallgemeinerte, projektive) Ebene, für k = n − 1 Hyperebene, für k = 1 Gerade in KPn. Auch die leere Menge wird hier als projektiver Teilraum betrachtet, dem der Nullraum von Kn + 1 und als Dimension − 1 zugeordnet wird.
von Kn + 1 ist ein k-dimensionaler projektiver Teilraum Sk von KPn zugeordnet. Man nennt Sk auch eine (verallgemeinerte, projektive) Ebene, für k = n − 1 Hyperebene, für k = 1 Gerade in KPn. Auch die leere Menge wird hier als projektiver Teilraum betrachtet, dem der Nullraum von Kn + 1 und als Dimension − 1 zugeordnet wird. - Die Schnittmenge von zwei projektiven Teilräumen ist wiederum ein projektiver Teilraum.
- Bildet man zu den Unterräumen, die zwei projektiven Räumen S1 und S2 zugeordnet sind, die lineare Hülle ihrer Vereinigungsmenge in Kn + 1, so gehört zu diesem Untervektorraum wieder ein projektiver Teilraum, der Verbindungsraum
 (auch als Summe S1 + S2 notiert) von S1 und S2.
(auch als Summe S1 + S2 notiert) von S1 und S2. - Für Schnitt und Verbindung von projektiven Teilräumen gilt die projektive Dimensionsformel:
-
 .
.
- Die Menge
 aller Teilräume des projektiven Raumes KPn bildet bezüglich der Verknüpfungen "Schnitt"
aller Teilräume des projektiven Raumes KPn bildet bezüglich der Verknüpfungen "Schnitt"  und "Verbindung"
und "Verbindung"  einen längenendlichen, modularen, komplementären Verband.
einen längenendlichen, modularen, komplementären Verband. - Jedem projektiven Punkt kann über seine Koordinaten eine homogene Koordinatengleichung zugeordnet werden, deren Lösungsmenge eine Hyperebene beschreibt. Durch die so definierten Hyperebenenkoordinaten bilden die Hyperebenen in KPn wiederum Punkte eines projektiven Raumes, des Dualraums (KPn)D.(→ siehe dazu Projektives Koordinatensystem#Koordinatengleichungen und Hyperebenenkoordinaten).
- Allgemeiner bildet die Menge der Hyperebenen, die einen festen k-dimensionalen Teilraum S enthalten, einen projektiven Raum, den man als Bündel, im Spezialfall k = n − 2 als Büschel von Hyperebenen bezeichnet. S heißt Träger des Bündels oder Büschels.
Literatur
- Albrecht Beutelspacher, Ute Rosenbaum: Projective geometry: from foundations to applications, Cambridge University Press, ISBN 978-0-521-48277-6
- Hermann Schaal: Lineare Algebra und analytische Geometrie, Band II, Vieweg 1980, ISBN 3-528-13057-1
Wikimedia Foundation.



