Prothsche Primzahlen

Prothsche Primzahlen

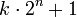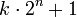Prothsche Primzahlen sind Primzahlen der Form k\cdot 2^n+1, wobei 2^n > k\ und k\ ungerade sein muss. Jede Primzahl lässt sich eindeutig in der Form k\cdot 2^n+1 schreiben; damit eine Primzahl eine Prothsche Primzahl ist, muss aber zusätzlich 2^n > k\ gelten.

Die Bedeutung der Prothschen Primzahlen liegt darin, dass François Proth (1852-1879) einen einfachen Test gefunden hat, mit dem sich nachweisen lässt, dass solche Zahlen Primzahlen sind. Viele der derzeit größten bekannten Primzahlen wurden mit diesem Test gefunden.

Die Prothschen Primzahlen spielen auch bei den Sierpinski-Zahlen insofern eine Rolle, als dass eine Folge von Zahlen der Form k \cdot 2^n+1\ frei von Prothschen Primzahlen sein muss, damit k\ eine Sierpinski-Zahl sein kann.

Unter den prothschen Primzahlen befinden sich auch Cullen-Primzahlen. Das sind Primzahlen der Form n\cdot 2^n+1.

In der folgenden Tabelle finden sich Primzahlen nach k geordnet. Primzahlen mit 2^n < k\ , die also keine Prothschen Primzahlen sind, stehen in Klammern.

Primzahlen nach k geordnet
k
1: 3, 5, 17, 257, 65537, …
3: (7), 13, 97, 193, 769, 12289, …
5: (11), 41, 641, 163841, …
7: (29), 113, 449, 114689, …
9: (19), (37), (73), 577, 1153, 18433, …
11: (23), (89), 353, 1409, 5767169, …
13: (53), 3329, 13313, …
15: (31), (61), 241, 7681, 15361, …
17: (137), 557057, …
19: 1217, 19457, …
21: (43), (337), 673, 2689, 10753, …
23: (47), 11777, …
… …

Weblinks


Wikimedia Foundation.

Игры ⚽ Поможем сделать НИР

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Prothsche Primzahl — Prothsche Primzahlen sind Primzahlen der Form , wobei und ungerade sein muss. Jede Primzahl lässt sich eindeutig in der Form schreiben; damit eine Primzahl eine Prothsche Primzahl ist, muss aber zusätzlich gelten. Die Bedeutung der Prothschen… …   Deutsch Wikipedia

  • Primzahlen — Eine Primzahl ist eine natürliche Zahl mit genau zwei natürlichen Zahlen als Teiler, nämlich der Zahl 1 und sich selbst. Die kleinsten Primzahlen sind 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 … (Folge A000040 in OEIS) Das Wort „Primzahl“ kommt aus… …   Deutsch Wikipedia

  • Mersenne-Primzahlen — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

  • Euklidisches Lemma — Eine Primzahl ist eine natürliche Zahl mit genau zwei natürlichen Zahlen als Teiler, nämlich der Zahl 1 und sich selbst. Die kleinsten Primzahlen sind 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 … (Folge A000040 in OEIS) Das Wort „Primzahl“ kommt aus… …   Deutsch Wikipedia

  • Primzahl — Die Zahl 12 ist keine Primzahl. Eine Primzahl ist eine natürliche Zahl, die größer als eins und ausschließlich durch sich selbst und durch eins teilbar ist. Eine Primzahl ist also eine natürliche Zahl mit genau zwei natürlichen Zahlen als Teiler …   Deutsch Wikipedia

  • GIMPS — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

  • Lucas-Lehmer Test — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

  • Mersenne-Zahl — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

  • Mersennesche Zahl — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

  • Mersennsche Primzahl — Eine Mersenne Zahl ist eine Zahl der Form 2n − 1. Im Speziellen bezeichnet man mit Mn = 2n − 1 die n te Mersenne Zahl. Die Primzahlen unter den Mersenne Zahlen werden Mersenne Primzahlen genannt. Die ersten acht Mersenne Primzahlen Mp sind 3, 7,… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”