Lucas-Lehmer Test

Eine Mersenne-Zahl ist eine Zahl der Form 2ⁿ − 1. Im Speziellen bezeichnet man mit M_n = 2ⁿ − 1 die n-te Mersenne-Zahl.

Die Primzahlen unter den Mersenne-Zahlen werden Mersenne-Primzahlen genannt. Die ersten acht Mersenne-Primzahlen M_p sind

3, 7, 31, 127, 8191, 131071, 524287, 2147483647 (Folge A000668 in OEIS) für p = 2, 3, 5, 7, 13, 17, 19, 31 (Folge A000043 in OEIS).

Ihren Namen haben diese Primzahlen von dem französischen Mönch und Priester Marin Mersenne, der im Vorwort seiner Cogitata Physico-Mathematica ^[1] behauptete, dass für p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 und 257 M_p eine Primzahl sei. Er irrte sich jedoch bei den Zahlen M₆₇ und M₂₅₇ und übersah die Mersenne-Primzahlen M₆₁, M₈₉ und M₁₀₇. Dass M₆₇ keine Primzahl ist, wurde erst im Jahre 1903 vom Mathematiker Frank Cole entdeckt. Um den Nachweis zu führen, dass M₂₅₇ keine Primzahl ist, wurde 1932 eine frühe Rechenmaschine verwendet.
Bei der Zahl M₆₇ handelt es sich möglicherweise um einen Lesefehler seitens Mersenne aus seiner Korrespondenz mit Bernard Frénicle de Bessy und Pierre de Fermat, wobei er p = 61 mit p = 67 verwechselte.

Eigenschaften der Mersenne-Zahlen

• Ist n eine zusammengesetzte Zahl, so ist auch M_n eine zusammengesetzte Zahl. Ist nämlich n = rs, dann lässt sich M_n als Produkt

$M_n = 2^{rs} - 1 = (2^r - 1) \cdot (2^{r(s-1)} + 2^{r(s-2)} + \ldots + 2^r+1)$

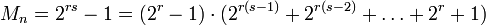
darstellen.

Daraus folgt unmittelbar, dass der Exponent p einer Mersenne-Primzahl M_p = 2^p − 1 selbst eine Primzahl ist. Der Umkehrschluss ist jedoch falsch, da beispielsweise 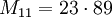$M_{11} = 23 \cdot 89$ keine Mersenne-Primzahl ist. Durch diese Eigenschaft wird die Suche nach Mersenne-Primzahlen erleichtert, da nur noch Mersenne-Zahlen mit Primzahlexponent betrachtet werden müssen.

• Ist n eine gerade Zahl und n+1 prim, so ist p = n+1 ein Teiler von M_n
  • z. B. M(10) = 1023 = 3*11*31 = M(2)*M(5)*11; M(12) = 4095 = 3*3*5*7*13 = 3*5*M(2)*M(3)*13

• Ist n eine ungerade Primzahl und q eine Primzahl und Teiler von M_n, so gilt q ≡ 1 (mod 2n) und q ≡ ±1 (mod 8).
  • z. B. M(11) = 2047 = 23*89; 23 = 2*11+1; 89 = 4*2*11+1

• Wenn p eine Primzahl ist und es gilt p ≡ 3 (mod 4), dann gilt: 2p+1 teilt die Mersenne-Zahl M_p ⇔ 2p+1 prim
  • z. B. 11 ist prim und lässt einen Rest von 3 bei Division mit 4; dann gilt: 23 teilt die Mersenne-Zahl M(11)=2047 ⇔ 23 (als Ergebnis von 2*11+1) ist prim

Diese Aussage wurde von Leonhard Euler formuliert, aber erst später von Joseph-Louis Lagrange bewiesen. (siehe auch Sophie-Germain-Primzahl)

• Ist n die m-te Potenz von 2, also n=2^m (mit m>0), so ist M_n das Produkt der Fermat-Zahlen F₀ bis F_m-1
  • z. B. M(16)=M(2⁴)=F(0)*F(1)*F(2)*F(3) = 3*5*17*257; M(32)=M(2⁵)=F(0)*F(1)*F(2)*F(3)*F(4) = 3*5*17*257*65537

• Ist M_p eine Primzahl > 3, dann ist M_p + 2 keine Primzahl; vielmehr ist M_p + 2 durch 3 teilbar, d. h. Mersenne-Primzahlen eignen sich nicht als Primzahlzwilling.

• Eine Mersenne-Primzahl kann keine Wieferich-Primzahl sein.

• Unter Annahme der erweiterten Riemannschen Vermutung lässt sich noch zeigen, dass die Summe der Kehrwerte der Teiler einer Mersenne-Primzahl

$\sum_{p<x, q|M_p}\frac{1}{q}$

für x gegen unendlich konvergiert.

Darstellung im Dualsystem

Die n-te Mersennezahl ist im Dualsystem eine Zahl mit n Einsen. Mersenne-Zahlen zählen deshalb zu den Zahlenpalindromen (in der Basis 2), genauer zu den Repunit-Zahlen (in der Basis 2); Mersenne-Primzahlen sind im besonderen Primzahlpalindrome (in der Basis 2).

Anwendungen

Neben der Tatsache, dass die größten bekannten Primzahlen Mersenne-Zahlen sind, spielen diese eine wichtige Rolle im Zusammenhang mit vollkommenen Zahlen. 2^{n - 1}(2ⁿ - 1) ist genau dann eine gerade vollkommene Zahl, wenn 2ⁿ − 1 eine Primzahl ist. In der Tabelle unten wird die vollkommene Zahl zur n-ten Mersennezahl mit P(n) bezeichnet.

Eine weitere Anwendung ist der Mersenne Twister, ein Pseudozufallszahlengenerator.

Die Suche nach Mersenne-Primzahlen

Für die Erzielung von Primzahl-Rekorden eignen sich die Mersenne-Primzahlen in mehrfacher Hinsicht besonders gut, weil

• zusammengesetzte Exponenten bedenkenlos unberücksichtigt bleiben können, weil diese keine Primzahlen generieren,
• die erforderlichen primen Exponenten quasi vorgefertigt zur Verfügung gestellt werden können - aus sogenannten Primzahlgeneratoren bzw. aus speziell zusammengestellten Mengen (Dateien),
  • aus diesen primen Exponenten die Sophie-Germain-Primzahlen mit p = 3 (mod 4) ausgesondert werden können (wie z. B. p = 11; Teiler 23), weil durch sie zusammengesetzte Mersenne-Zahlen generiert werden mit Teiler 2*p + 1
• durch den funktionalen Zusammenhang die Größenordnung der Primzahl exponentiell - nämlich zur Basis zwei - mit dem Argument p anwächst,
• ein einfacher und schneller Faktor-Finder vorgeschaltet werden kann, der den Prüfling auf kleinere Primfaktoren vorprüft,
• mit dem nachfolgend beschriebenen Lucas-Lehmer-Test ein relativ einfacher und effektiver Primzahltest zur Verfügung steht,
• die Wahrscheinlichkeit, unter den Mersenne-Zahlen eine Primzahl zu finden, für größer angenommen wird als unter einer zufällig ausgewählten ungeraden Zahl derselben Größenordnung.

Der Lucas-Lehmer-Test

Der Lucas-Lehmer-Test ist zum Testen von Mersenne-Zahlen ab M₃ geeignet. Er basiert ganz wesentlich darauf, dass die Mersenne-Zahlen im Dualsystem nur aus lauter Einsen bestehen. Er funktioniert wie folgt:

Sei p ungerade und prim. Ferner sei die rekursive Folge S(k+1) definiert durch S(1) = 4, S(k+1) = S(k)²–2

Dann gilt: M_p = 2^p–1 ist genau dann eine Primzahl, wenn S(p–1) durch M_p teilbar ist.

In dieser von Derrick Henry Lehmer gefundenen Form, die auf Édouard Lucas zurück geht, ist die Anwendung allerdings unpraktisch, weil die Zahlen S(k) sehr schnell sehr groß werden. Deshalb werden heutzutage bereits alle Zwischenschritte modulo M_p ausgerechnet, so dass große Zahlen vermieden werden:

Sei S(1) = 4, S(k+1) = S(k)²–2 mod M_p

Ist S(p–1) = 0 dann ist M_p eine Primzahl.

Beispiele

Wir prüfen mit diesem Verfahren, ob M₅ = 2⁵–1 = 31 eine Primzahl ist:

 S(1) = 4
 S(2) = ( 4² - 2) mod 31 = 14
 S(3) = (14² - 2) mod 31 =  8
 S(4) = ( 8² - 2) mod 31 =  0

Da S(4) = 0 ist, ist M₅ = 31 eine Primzahl.

Wir prüfen mit diesem Verfahren, ob M₁₁ = 2¹¹–1 = 2047 = 23 * 89 eine Primzahl ist:

 S( 1) = 4
 S( 2) = (   4² - 2) mod 2047 =   14
 S( 3) = (  14² - 2) mod 2047 =  194
 S( 4) = ( 194² - 2) mod 2047 =  788
 S( 5) = ( 788² - 2) mod 2047 =  701
 S( 6) = ( 701² - 2) mod 2047 =  119
 S( 7) = ( 119² - 2) mod 2047 = 1877
 S( 8) = (1877² - 2) mod 2047 =  240
 S( 9) = ( 240² - 2) mod 2047 =  282
 S(10) = ( 282² - 2) mod 2047 = 1736

Da S(10) > 0 ist, ist M₁₁ = 2047 keine Primzahl.

Wir prüfen mit diesem Verfahren, ob M₁₉ = 2¹⁹–1 = 524287 eine Primzahl ist:

 S( 1) = 4
 S( 2) = (      4² - 2) mod 524287 =     14
 S( 3) = (     14² - 2) mod 524287 =    194
 S( 4) = (    194² - 2) mod 524287 =  37634
 S( 5) = (  37634² - 2) mod 524287 = 218767
 S( 6) = ( 218767² - 2) mod 524287 = 510066
 S( 7) = ( 510066² - 2) mod 524287 = 386344
 S( 8) = ( 386344² - 2) mod 524287 = 323156
 S( 9) = ( 323156² - 2) mod 524287 = 218526
 S(10) = ( 218526² - 2) mod 524287 = 504140
 S(11) = ( 504140² - 2) mod 524287 = 103469
 S(12) = ( 103469² - 2) mod 524287 = 417706
 S(13) = ( 417706² - 2) mod 524287 = 307417
 S(14) = ( 307417² - 2) mod 524287 = 382989
 S(15) = ( 382989² - 2) mod 524287 = 275842
 S(16) = ( 275842² - 2) mod 524287 =  85226
 S(17) = (  85226² - 2) mod 524287 = 523263
 S(18) = ( 523263² - 2) mod 524287 =      0

Da S(18) = 0 ist, ist M₁₉ = 524287 eine Primzahl (seit 1603 bekannt).

Literatur zum Lucas-Lehmer-Test

• Théorie des Fonctions Numériques Simplement Périodiques, É. Lucas, Amer. Journ. of Math., 1, 289–
• An extended theory of Lucas' functions, D. H. Lehmer, Annals of mathematics, 31, 419–

Suche nach Mersenne-Primzahlen: GIMPS

Bisher kennt man 46 Mersenne-Primzahlen. Mit Computerhilfe versucht man, weitere Mersenne-Primzahlen zu finden. Da es sich um sehr große Zahlen handelt – die 46. Mersenne-Primzahl hat knapp 13 Millionen Ziffern im Dezimalsystem – sind die Berechnungen (zeit- und organisations-)aufwendig. Rechenoperationen mit derart großen Zahlen werden von Computern nicht von Haus aus unterstützt. Man muss die Zahlen in großen Feldern abspeichern und die damit erforderlichen Grundrechenarten programmieren. Dies führt zu langen Programmlaufzeiten.

GIMPS (engl.: Great Internet Mersenne Prime Search) versucht daher, weltweit möglichst viele Computer an den Berechnungen zu beteiligen und stellt die erforderliche Software (Prime95) für eine Reihe von Plattformen (Windows, Unix, Linux ...) zur Verfügung. Jeder kann mitmachen, sofern er einen Rechner mit (zeitweise) freien CPU-Kapazitäten besitzt. Dazu muss man sich von der Website die Software herunterladen und dann installieren. Danach meldet man sich bei GIMPS und lässt sich eine Zahl geben, die man untersuchen soll. Wenn die Berechnungen erledigt sind (meist nach mehreren Monaten) meldet man das Ergebnis bei GIMPS zurück. Man bekommt dabei im Laufe der Computeranalyse auch Wahrscheinlichkeiten mitgeteilt: die Wahrscheinlichkeit, eine Primzahl zu finden (sehr klein, unter 1 %); die Wahrscheinlichkeit, einen Faktor zu finden (größer). Diese Wahrscheinlichkeit soll einem die Erfolgsaussichten für das Finden einer Primzahl deutlich machen.

Vermutungen zu den Mersenne-Zahlen

• Gibt es unendlich viele Mersenne-Primzahlen? Man vermutet aufgrund von plausiblen Heuristiken, dass es etwa 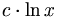$c \cdot \ln x$ viele Mersenne-Primzahlen M_p gibt mit p < x. Wenn dies der Fall ist, so gibt es tatsächlich unendlich viele Mersenne-Primzahlen.

• Gibt es unendlich viele Mersenne-Zahlen M_p mit p prim, die keine Primzahlen sind? Auch hier vermutet man als Antwort ja. Dies würde zum Beispiel aus der Vermutung, dass es unendlich viele Sophie-Germain-Primzahlen gibt, die kongruent 3 modulo 4 sind, folgen.

• Sind alle Mersenne-Zahlen M_p mit p prim quadratfrei, d. h. kommt in der Primfaktorzerlegung der Zahl jeder Primfaktor genau einmal vor? Man konnte bisher noch nicht einmal beweisen, dass dies für unendlich viele Mersenne-Zahlen gilt.

• Gilt die "neue Mersenne-Vermutung"? Die Folge von Mersenne-Primzahlen, die Mersenne angab, lässt vermuten, dass er meinte, dass eine Mersenne-Zahl M_p mit p prim genau dann prim ist, wenn p=2^k±1 oder p=4^k±3. Da diese Aussage nicht gilt, stellten P. Bateman, J. Selfridge und S. Wagstaff die neue Mersenne-Vermutung auf.

Diese besagt, dass aus zwei der folgenden drei Aussagen bereits die dritte folgt:

1. n = 2^k ± 1 oder n = 4^k ± 3
2. 2ⁿ – 1 ist eine (Mersenne) Primzahl
3. (2ⁿ+1)/3 ist eine Primzahl

s. auch: neue Mersenne Vermutung (engl.)

• Sind alle Glieder der Folge C(0) = 2, C(k+1) = 2^C(k)–1 Primzahlen? Die stärkere Vermutung, dass alle Zahlen M_Mp Primzahlen sind, für die M_p eine Primzahl ist, konnte inzwischen für p=13 widerlegt werden. Diese letzteren Zahlen nennt man doppelte Mersenne-Zahlen. Auch hier ist noch nicht bekannt, ob es unendlich viele Primzahlen darunter gibt.

Geschichte der Mersenne-Primzahlen

Dieser Artikel oder Abschnitt besteht hauptsächlich aus Listen, an deren Stelle besser Fließtext stehen sollte.

Jahr	Ereignis
bis 1536	Man glaubt, dass für alle Primzahlen p gilt, 2p–1 sei prim.
1536	Der deutsche Rechenmeister Ulrich Rieger (lat. Hudalrichus Regius) veröffentlicht in seinem Rechenbuch Utriusque Arithmetices epitome[2] als erster die fünfte vollkommene Zahl 212•(213–1) = 4.096•8.191 = 33.550.336 in gedruckter Form. Nachdem die Zahlen 511 und 2.047 in seiner tabellarischen Übersicht nicht vorkommen, darf man annehmen, dass er 211–1 = 2047 = 23•89 als zusammengesetzt erkannt hat, obgleich er dies nicht extra erwähnt.
1555	Johann Scheubel veröffentlicht in seiner deutschen Übersetzung der Bücher VII-IX von Euklids Elementen die nächsten beiden vollkommenen Zahlen 216•(217–1) = 65.536•131.071 = 8.589.869.056 und 218•(219–1) = 262.144•524.287 = 137.438.691.328.[3] Die zweiten Faktoren sind die Mersenneschen Primzahlen M17 und M19. Allerdings hat er sowohl 211–1 = 2047 = 23•89, als auch 215–1 = 32.767 = 7•31•151 nicht als zusammengesetzt erkannt, dafür aber 221–1 = 2.097.151 = 72•127•337. (Die Zerlegungen gibt er allerdings an dieser Stelle nicht an.) Er erhält in seinem Werk also fälschlicherweise neun, anstatt der korrekten sieben vollkommenen Zahlen.
1603	Pietro Cataldi (1548–1626) zeigt, dass 2n–1 Primzahlen sind für n = 17, 19. Fälschlicherweise glaubt er dies auch für n = 23, 29, 31 und 37 (ist nur für n = 31 korrekt).
1640	Fermat widerlegt Cataldi für n = 23 und n = 37: 223–1 = 47 * 178481 und 237–1 = 223 * 616318177 sind keine Primzahlen.
1644	Mersenne behauptet, 2n–1 sei prim für n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 und 257, jedoch nicht prim für alle anderen natürlichen Zahlen kleiner als 257 (Vorwort zu seinem Werk "Cogitata Physica-Mathematica"). Dies ist allerdings falsch, denn 2n–1 ist prim sowohl für n = 61 (was 1883 bemerkt wird) als auch für n = 89,107 (wird erst nach 1900 nachgewiesen).
1738	Euler widerlegt Cataldi für n = 29: 229-1 =233 * 1103 * 2089
1750	Euler bestätigt, dass Cataldi für n=31 richtig lag: 231–1 ist prim.
1870	Édouard Lucas (1842–1891) formuliert die theoretischen Grundlagen für den Lucas-Lehmer Test.
1876	Lucas bestätigt Mersenne: 2127–1 ist prim.
1883	M. Pervouchine (orthodoxer Priester in Perm/Russland) zeigt, dass 261–1 prim ist (Widerspruch zu Mersenne).
1911	R.E. Powers widerspricht Mersenne für n = 89: 2n–1 ist prim.
1914	Powers widerspricht Mersenne auch für n = 107: 2n–1 ist prim. Fast gleichzeitig kommt auch E. Fauquembergue zu dieser Aussage.
1930	Lehmer (1905-1991) formuliert den Lucas-Lehmer Test.
1932	Lehmer zeigt: M(149) und M(257) sind nicht prim.
1934	Powers zeigt: M(241) ist nicht prim.
1944	H.S.Uhler zeigt: M(157) und M(167) sind nicht prim.
1945	H.S.Uhler zeigt: M(229) ist nicht prim.
1947	H.S.Uhler zeigt: M(199) ist nicht prim.
1947	Der Bereich von 1 bis 258 wird vollständig überprüft. Man kennt nun die Mersenne-Primzahlen M(n) für n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 und 127.
1951	Beginn des Einsatzes von Computern, die Länge der größten bekannten Primzahl steigt bis 1952 von 39 Stellen auf 687 Dezimalstellen.
1963	Gillies entdeckt M(11.213) mit 3.376 Stellen.
1996	Joel Armengaud und George Woltman entdecken mit GIMPS M(1.398.269) mit 420.921 Stellen.
1999	Mit M(6.972.593), die 2.098.960 Stellen hat, kennt man erstmals eine Primzahl mit mehr als 1 Million Stellen.
2004	Es wird nachgewiesen, dass M(24.036.583), eine Zahl mit 7.235.733 Stellen, prim ist.
2005	Im Februar wird vom GIMPS-Projekt die 42. Mersenne-Primzahl entdeckt: M(25.964.951) hat 7.816.230 Stellen. Ebenfalls vom GIMPS-Projekt wird im Dezember die 43. Mersenne-Primzahl entdeckt: M(30.402.457) hat 9.152.052 Stellen.
2006	Am 4. September vermeldet das GIMPS-Projekt die Entdeckung der 44. Mersenne-Primzahl M(32.582.657) mit 9.808.358 Stellen.
2008	Am 16. September werden vom GIMPS-Projekt die 45. und die 46. bekannte Mersenne-Primzahl veröffentlicht: M(37.156.667) (entdeckt am 6. September) mit 11.185.272 Stellen und M(43.112.609) (entdeckt am 23. August) mit 12.978.189 Stellen.

Liste aller bekannten Mersenne-Primzahlen

Nr.	n	Anzahl Ziffern von M(n)	Anzahl Ziffern der perfekten Zahl P(n)	Jahr	Entdecker
1	2	1	1	-	-
2	3	1	2	-	-
3	5	2	3	-	-
4	7	3	4	-	-
5	13	4	8	1456	-
6	17	6	10	1555	Johann Scheubel
7	19	6	12	1555	Scheubel
8	31	10	19	1772	Leonhard Euler
9	61	19	37	1883	Ivan Mikheevich Pervushin
10	89	27	54	1911	R. E. Powers
11	107	33	65	1914	Powers
12	127	39	77	1876	Édouard Lucas
13	521	157	314	1952	Raphael M. Robinson
14	607	183	366	1952	Robinson
15	1279	386	770	1952	Robinson
16	2203	664	1327	1952	Robinson
17	2281	687	1373	1952	Robinson
18	3217	969	1937	1957	Hans Riesel
19	4253	1281	2561	1961	Alexander Hurwitz
20	4423	1332	2663	1961	Hurwitz
21	9689	2917	5834	1963	Donald B. Gillies
22	9941	2993	5985	1963	Gillies
23	11.213	3376	6751	1963	Gillies
24	19.937	6002	12003	1971	Bryant Tuckerman
25	21.701	6533	13066	1978	Landon Curt Noll und Laura Nickel
26	23.209	6987	13973	1979	Noll
27	44.497	13.395	26790	1979	David Slowinski und Harry Nelson
28	86.243	25.962	51924	1982	Slowinski
29	110.503	33.265	66530	1988	Walter Colquitt und Luther Welsh Jr.
30	132.049	39.751	79502	1983	Slowinski
31	216.091	65.050	130100	1985	Slowinski
32	756.839	227.832	455663	1992	Slowinski und Paul Gage
33	859.433	258.716	517430	1994	Slowinski und Gage
34	1.257.787	378.632	757263	1996	Slowinski und Gage
35	1.398.269	420.921	841842	1996	Joel Armengaud und George Woltman (GIMPS)
36	2.976.221	895.932	1.791.864	1997	Gordon Spence und Woltman (GIMPS)
37	3.021.377	909.526	1.819.050	1998	Roland Clarkson, Woltman und Scott Kurowski (GIMPS, PrimeNet)
38	6.972.593	2.098.960	4.197.919	1999	Nayan Hajratwala, Woltman und Kurowski (GIMPS, PrimeNet)
39	13.466.917	4.053.946	8.107.892	2001	Michael Cameron, Woltman und Kurowski (GIMPS, PrimeNet)
40?	20.996.011	6.320.430	12.640.859	2003	Michael Shafer, Woltman und Kurowski (GIMPS, PrimeNet)
41?	24.036.583	7.235.733	14.471.466	2004	Josh Findley, Woltman und Kurowski (GIMPS, PrimeNet)
42?	25.964.951	7.816.230	15.632.458	2005	Martin Nowak, Woltman und Kurowski (GIMPS, PrimeNet)
43?	30.402.457	9.152.052	18.304.103	2005	Curtis Cooper, Steven Boone, Woltman und Kurowski (GIMPS, PrimeNet)
44?	32.582.657	9.808.358	19.616.714	2006	Cooper, Boone, Woltman und Kurowski (GIMPS, PrimeNet)
45?	37.156.667	11.185.272	22.370.543	2008	Hans-Michael Elvenich, Woltman und Kurowski (GIMPS, PrimeNet)
46?	43.112.609	12.978.189	25.956.377	2008	Edson Smith, Woltman und Kurowski (GIMPS, PrimeNet)

Bisher (Stand 7. Januar 2009) ist unbekannt, ob es zwischen n=13.466.917 und n=43.112.609 neben den sechs bekannten Mersenne-Primzahlen noch weitere gibt; deshalb ist die Nummerierung ab Nr. 40 noch ungewiss (und mit einem '?' versehen).

Quellen

1. ↑ Marin Mersenne: Cogitata Physico-Mathematica. In quibus tam naturae quàm artis effectus admirandi certissimis demonstrationibus explicantur. Paris: Bertier, 1644, Praefatio generalis, Nr. XIX.
2. ↑ Hudalrichus Regius: Vtrivsque Arithmetices epitome ex uarijs authoribus concinnata. Straßburg: Bartholomäus Grüninger, 1536, S. VIIIv-IXv, Kap. 6 (De perfecto [Über die vollkommenen Zahlen]).
3. ↑ Johann Scheubel: Das sibend, acht vnd neunt buch, des hochberümbten Mathematici Euclidis Megarensis, in welchen der operationen vnnd regulen aller gemainer rechnung, vrsach grund vnd fundament, angezaigt wirt, zu gefallen allen den, so die kunst der Rechnung liebhaben [...] auß dem latein ins teütsch gebracht, vnnd mit gemainen exemplen also illustrirt vnnd an tag geben, das sy ein yeder gemainer Rechner leichtlich verstehn, vnnd ime nutz machen kan. Augsburg: Valentin Ottmar, 1555, S. CCXXXI-CXXXIIII (Euklid IX, 36), hier S. CCXXXIII.

siehe auch

• Kreisteilungspolynom
• Repunit
• Fermat-Zahl
• Prothsche Primzahl
• Riesel-Zahl
• GNU Multiple Precision Arithmetic Library
• Mathematische Konstante
  • Erdős–Borwein Konstante

Weblinks

• prime Mersenne Numbers - History, Theorems and Lists (englisch)
• Die Deutsche Great Internet Mersenne Prime Search (GIMPS) Homepage
• prime Mersenne Numbers - History, Theorems and Lists Explanation (englisch)
• Mersenne Primzahlen Bibliografie mit Links auf die Original-Veröffentlichungen (engl.)
• Wie eine neue Mersenne Primzahl entdeckt wurde - dpa-Hintergrundbericht
• prime Mersenne numbers - Wolframresearch/Mathematica (englisch)
• M_q = (8x)^2 - (3qy)^2 Mersenne Proof (PDF)
• M_q = x^2 + d.y^2 Math Thesis (PDF)
• mprint5 - schnelle Berechnung der Mersenne-Primzahlen von dem Finnen Mikko Tommila