Pseudoranging

Pseudoranging ist ein Verfahren der Satelliten-Ortung, bei dem sogenannte „Pseudostrecken“ zur Ortsbestimmung herangezogen werden. Sie weichen von den wahren Distanzen um einen konstanten, aber vorerst unbekannten Betrag ab.

Zunächst wird die Laufzeit der Funksignale von den verwendeten Satelliten zum Empfänger des Beobachters gemessen. Daraus ergeben sich die momentanen Entfernungen zu den Satelliten, die jedoch noch mit Fehlern der Uhren (Satellit, Empfänger) und anderen kleinen Einflüssen behaftet sind.

Sind jedoch die Satellitenuhren untereinander genau synchronisiert, so sind alle gemessenen Laufzeiten praktisch nur mehr vom Synchronisationsfehler der Empfängeruhr betroffen – d.h. alle um nahezu denselben Betrag verfälscht. Diese um eine Konstante zu langen oder zu kurzen Distanzen werden Pseudostrecken (Pseudo Ranges) genannt.

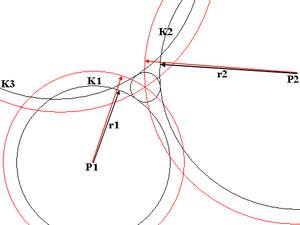
Bogenschnitt mit wahren und mit Pseudostrecken

Die Position eines Punktes in der Ebene (2D-Raum) lässt sich aus zwei Strecken mit dem Bogenschnitt bestimmen: dem Schnitt zweier Kreise um die jeweils angemessenen Punkte. Zwar gibt es zwei Schnittpunkte, doch lässt sich diese Zweideutigkeit des Standpunkts immer klären.

Punktbestimmung (2-dimensional) mit 3 Pseudostrecken: die Distanzen r1, r2 von den Fixpunkten P1, P2 sind um einen kleinen Betrag verfälscht. Der Schnitt der zugehörigen (schwarzen) Kreise K1, K2 ist daher zu korrigieren (rote Kreise), was durch eine 3.Messung (Kreis K3) möglich wird.

Wenn nun die 2 Strecken um eine Konstante verfälscht, also Pseudostrecken sind, wird auch der Schnittpunkt fehlerhaft (speziell bei schleifenden Schnitten). Hat man jedoch eine dritte (ebenso viel verfälschte) Strecke gemessen, lässt sich die Konstante leicht ermitteln: die 3 Kreise schneiden sich nicht in einem Punkt, sondern bilden ein kleines, krummliniges Fehlerdreieck. Sein Inkreismittelpunkt ist der gesuchte Punkt.
Im Bild entspricht die Konstante der Korrektion von den schwarzen Kreisen K1, K2, K3 auf die roten Kreise.

Räumlicher Bogenschnitt

Im dreidimensionalen Raum ist die Situation analog, nur werden zur Ortsbestimmung drei Strecken (bzw. 4 Pseudostrecken) benötigt. Man schlägt um die angemessenen Punkte jeweils eine Kugel mit der Strecke als Radius, wobei sich immer zwei Kugeln entlang eines Kreises schneiden, der seinerseits die 3.Kugel im gesuchten Punkt (und einem zweiten) schneidet.

Beim Vorliegen von Pseudostrecken sind alle 3 Kugelradien um denselben Betrag verfälscht, der mittels einer vierten Kugel (Distanz zu einem vierten Punkt bzw. Satellit) bestimmbar ist.

Anwendung bei GPS

Dieses Messprinzip wird bei der Satellitennavigation des Global Positioning System angewendet. Die Atomuhren aller GPS-Satelliten (bzw. bei GLONASS) laufen in hohem Maße synchron (Genauigkeit 10^-14), was sogar bei Lichtgeschwindigkeit nur Fehler weit unter dem Millimeter bedeutet. Die Streckenkorrektur (Konstante in allen Pseudostrecken) hängt also nur von der Uhrkorrektur der Empfänger-Quarzuhr ab und kann für die kurze Zeit der Messungen als konstant gelten.

Damit lässt sich der Uhrfehler auf analoge Art wie oben bestimmen und stellt die 4. Unbekannte dar – neben den 3 zu bestimmenden Koordinaten des eigenen Standpunktes.

De facto kommen noch weitere winzige Fehlereinflüsse dazu, die sich aber gut modellieren lassen. Dazu gehören eine leichte Drift der Empfängeruhr und eine Abweichung der Erdatmosphäre vom Idealzustand (Funksignale geringfügig langsamer als im Vakuum, siehe Brechzahl). Was jedoch nicht (oder erst im nachhinein) zu eliminieren ist, sind die Fehler in den Satellitenbahnen.

Die Methode der Streckenkorrektionen (Pseudorange Correction) lässt sich auf ähnliche Weise anwenden, wenn man die Position einer Referenzstation schon genau kennt. Verschiedene Navigationsdienste senden diese Korrektionen per Funk aus, wodurch die Fehler der Ortung von einigen Zehnermetern auf ein Zehntel oder Hundertstel sinken (DGPS).