- Quotientenregel
-
Die Quotientenregel ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Quotienten von Funktionen auf die Berechnung der Ableitung der einzelnen Funktionen zurück.
Sind die Funktionen u(x) und v(x) von einem Intervall D in die reellen oder komplexen Zahlen an der Stelle x = xa mit
 differenzierbar, dann ist auch die Funktion f mit
differenzierbar, dann ist auch die Funktion f mitan der Stelle xa differenzierbar und es gilt:
 .
.
In Kurzschreibweise:
Erklärung
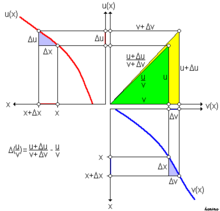
Der Quotient
 kann als Steigung in einem Steigungsdreieck gedeutet werden, dessen Katheten u(x) und v(x) sind (siehe Abbildung). Wenn x um Δx anwächst, ändert sich u um Δu und v um Δv. Die Änderung der Steigung ist dann
kann als Steigung in einem Steigungsdreieck gedeutet werden, dessen Katheten u(x) und v(x) sind (siehe Abbildung). Wenn x um Δx anwächst, ändert sich u um Δu und v um Δv. Die Änderung der Steigung ist dannDividiert man durch Δx, so folgt
Bildet man nun Limes Δx gegen 0, so wird
wie behauptet.
Beweis
Gegeben sei
 Nach der Produktregel gilt:
Nach der Produktregel gilt:Nach der Kehrwertregel (ergibt sich z.B. direkt oder mit Hilfe der Kettenregel)
folgt:
Ein alternativer Beweis gelingt nur mit der Produktregel durch Ableiten der Funktionsgleichung

folglich:
Literatur
Die Quotientenregel für Funktionen wird in jedem Buch erläutert, das Differentialrechnung in allgemeiner Form behandelt.
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg, Braunschweig 72004. ISBN 3-528-67224-2
- Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
- C. H. Edwards Jr.: The Historical Development of the Calculus, 1979, Springer New York
Wikimedia Foundation.