- Produktregel
-
Die Produktregel oder Leibnizregel (nach G. W. Leibniz) ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Produktes von Funktionen auf die Berechnung der Ableitung der einzelnen Funktionen zurück.
Sind die Funktionen u(x) und v(x) von einem Intervall D in die reellen oder komplexen Zahlen an der Stelle x = xa differenzierbar, so ist auch die Funktion
an der Stelle x = xa differenzierbar, und es gilt
oder kurz:
 .
.
Eine Anwendung der Produktregel in der Integralrechnung ist die Methode der partiellen Integration. Im Falle von konstanten Faktoren geht die Produktregel in die einfachere Faktorregel über.
Inhaltsverzeichnis
Anwendungsbeispiele
Im Folgenden sei stets f(x) = u(x)v(x).
- Ist u(x) = x und v(x) = x, so erhält man aus der Kenntnis von u'(x) = 1 und v'(x) = 1 mit der Produktregel die Aussage
- Ist u(x) = x und
 , so ist f(x) = u(x)v(x) = 1, also ist
, so ist f(x) = u(x)v(x) = 1, also ist
-
- und durch Umformen erhält man die Aussage
Erklärung und Beweis
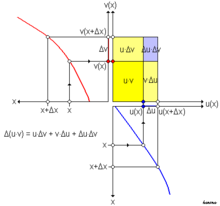
Das Produkt zweier reeller Funktionen u(x) und v(x) kann als Flächeninhalt eines Rechtecks mit den Seiten u und v gedeutet werden. Ändert sich nun x um Δx, so ändert sich u(x) um Δu und v(x) um Δv. Die Änderung des Flächeninhalts (also
 ) setzt sich dann (siehe Abbildung) zusammen aus:
) setzt sich dann (siehe Abbildung) zusammen aus: .
.
Dividiert man durch Δx so ergibt sich
Für Δx gegen 0 wird der letzte Summand schneller kleiner als die beiden anderen und man erhält
wie behauptet. Dieses ist auch im Wesentlichen die Argumentation, wie sie sich in einem ersten Beweis der Produktregel 1677 in einem Manuskript von Leibniz findet. Die Produktregel, die er dort gemeinsam mit der Quotientenregel beweist, war damit eine der ersten Regeln zur Anwendung der Infinitesimalrechnung, die er herleitete. Er benutzte allerdings keinen Grenzwert, sondern noch Differentiale und schloss, dass
 wegfällt, weil es im Vergleich zu den anderen Faktoren infinitesimal klein sei. Euler benutzte noch dasselbe Argument, erst bei Cauchy findet sich ein Beweis mit Grenzwerten.
wegfällt, weil es im Vergleich zu den anderen Faktoren infinitesimal klein sei. Euler benutzte noch dasselbe Argument, erst bei Cauchy findet sich ein Beweis mit Grenzwerten.Gegeben sei die Funktion f durch
 . Die Ableitung von f ist dann durch den Grenzwert des Differenzenquotienten
. Die Ableitung von f ist dann durch den Grenzwert des Differenzenquotientengegeben. Addition und Subtraktion des Terms
 liefert
liefertDas Bilden des Grenzwerts liefert dann die Produktregel
 .
.Verallgemeinerungen
Produkte von Vektoren und Matrix-Vektor-Produkte
Beim Beweis der Produktregel werden aus den Werten von
 Linearkombinationen (Summen, Differenzen, Produkte mit Zahlen) gebildet, ebenso aus den Werten von
Linearkombinationen (Summen, Differenzen, Produkte mit Zahlen) gebildet, ebenso aus den Werten von  . Die Rollen von
. Die Rollen von  und
und  sind dabei klar getrennt:
sind dabei klar getrennt:  ist der linke Faktor,
ist der linke Faktor,  der rechte. Der Beweis überträgt sich deswegen auf alle Produktbildungen, die sowohl im linken als auch im rechten Faktor linear sind. Insbesondere gilt die Produktregel auch für
der rechte. Der Beweis überträgt sich deswegen auf alle Produktbildungen, die sowohl im linken als auch im rechten Faktor linear sind. Insbesondere gilt die Produktregel auch für- Skalarprodukte von zwei Vektoren
- Vektorprodukte (Kreuzprodukte) von zwei Vektoren
- Matrix-Vektor-Produkte
Vektoren bzw. Matrizen sind dabei als Funktionen einer unabhängigen Variablen zu verstehen.
Mehr als zwei Faktoren
Die Produktregel kann sukzessive auch auf mehrere Faktoren angewandt werden. So wäre
 und
und usw.
usw.
Allgemein ist für eine Funktion
 , die sich als Produkt von n Funktionen fi schreiben lässt, die Ableitung
, die sich als Produkt von n Funktionen fi schreiben lässt, die Ableitung .
.
Haben die Funktionen keine Nullstellen, so kann man diese Regel auch in der übersichtlichen Form
schreiben; derartige Brüche bezeichnet man als logarithmische Ableitungen.
Höhere Ableitungen
Auch die Regel für Ableitungen n-ter Ordnung für ein Produkt aus zwei Funktionen war schon Leibniz bekannt und wird entsprechend manchmal ebenfalls als Leibnizsche Regel bezeichnet. Sie ergibt sich aus der Produktregel mittels vollständiger Induktion zu
Die hier auftretenden Ausdrücke der Form
 sind Binomialkoeffizienten. Die obige Formel enthält die eigentliche Produktregel als Spezialfall. Sie hat auffallende Ähnlichkeit zum binomischen Lehrsatz
sind Binomialkoeffizienten. Die obige Formel enthält die eigentliche Produktregel als Spezialfall. Sie hat auffallende Ähnlichkeit zum binomischen LehrsatzDiese Ähnlichkeit ist kein Zufall, der übliche Induktionsbeweis läuft in beiden Fällen vollkommen analog; man kann die Leibnizregel aber auch mithilfe des binomischen Satzes beweisen.
Höherdimensionaler Definitionsbereich
Verallgemeinert man auf Funktionen mit höherdimensionalem Definitionsbereich, so lässt sich die Produktregel wie folgt formulieren: Es seien
 eine offene Teilmenge,
eine offene Teilmenge,  differenzierbare Funktionen und
differenzierbare Funktionen und  ein Richtungsvektor. Dann gilt die Produktregel für die Richtungsableitung:
ein Richtungsvektor. Dann gilt die Produktregel für die Richtungsableitung:Entsprechend gilt für die Gradienten
In der Sprache der differenzierbaren Mannigfaltigkeiten lauten diese beiden Aussagen:
- Sind x ein Tangentialvektor und u,v lokale differenzierbare Funktionen, dann gilt
- Sind u,v lokale differenzierbare Funktionen, so gilt die folgende Beziehung zwischen den äußeren Ableitungen:
Holomorphe Funktionen
Die Produktregel gilt analog für komplex differenzierbare Funktionen: Es sei
 und
und  holomorph. Dann ist fg holomorph, und es gilt
holomorph. Dann ist fg holomorph, und es gilt- (fg)' = f'g + fg'.
Allgemeine differenzierbare Abbildungen
Es seien
 ein offenes Intervall, B eine Banachalgebra (z. B. die Algebra der reellen oder komplexen
ein offenes Intervall, B eine Banachalgebra (z. B. die Algebra der reellen oder komplexen  -Matrizen) und
-Matrizen) und  differenzierbare Funktionen. Dann gilt
differenzierbare Funktionen. Dann giltdabei bezeichnet »·« die Multiplikation in der Banachalgebra.
Sind allgemeiner
 und
und  Banach-Räume,
Banach-Räume,  und
und  differenzierbare Funktionen, so gilt ebenfalls eine Produktregel, wobei die Funktion des Produktes von einer Bilinearform
differenzierbare Funktionen, so gilt ebenfalls eine Produktregel, wobei die Funktion des Produktes von einer Bilinearform  übernommen wird. Von dieser wird verlangt, dass sie stetig ist, also beschränkt:
übernommen wird. Von dieser wird verlangt, dass sie stetig ist, also beschränkt: für alle
für alle 
mit einer festen Konstante C. Dann gilt die Produktregel
Entsprechende Aussagen gelten für höherdimensionale Definitionsbereiche.
Abstraktion: Derivationen
Allgemein nennt man Abbildungen D, die die Produktregel
erfüllen, Derivationen. (Die Reihenfolge der Faktoren ist hier für den Fall einer Derivation
 mit einer Algebra A und einem A-Linksmodul M gewählt.)
mit einer Algebra A und einem A-Linksmodul M gewählt.)Im Zusammenhang mit
 - oder
- oder  -graduierten Algebren („Superalgebren“) muss der Begriff der Derivation jedoch durch den der Antiderivation ersetzt werden; die entsprechende Gleichung lautet dann
-graduierten Algebren („Superalgebren“) muss der Begriff der Derivation jedoch durch den der Antiderivation ersetzt werden; die entsprechende Gleichung lautet dannfür homogene Elemente u,v; dabei bezeichnet | u | den Grad von u. Das prominenteste Beispiel einer Antiderivation ist die äußere Ableitung für Differentialformen
Literatur
Die Produktregel für Funktionen wird in jedem Buch erläutert, das Differentialrechnung in allgemeiner Form behandelt.
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg, Braunschweig 72004. ISBN 3-528-67224-2
- Otto Forster: Analysis 2. Differentialrechnung im Rn. Gewöhnliche Differentialgleichungen. Vieweg, Braunschweig 62005. ISBN 3-528-47231-6
- Konrad Königsberger: Analysis. 2 Bde. Springer, Berlin 2004, ISBN 3-540-41282-4
- C. H. Edwards Jr.: The Historical Development of the Calculus, 1979, Springer New York
Siehe auch
Weblinks

Dieser Artikel wurde in die Liste der lesenswerten Artikel aufgenommen. Kategorien:- Wikipedia:Lesenswert
- Analysis
Wikimedia Foundation.