Rayleigh-Jeans-Gesetz

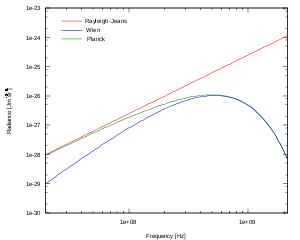Vergleich des Rayleigh-Jeans-Gesetzes mit dem Wienschen- und dem planckschen Strahlungsgesetz, für einen schwarzen Körper der Temperatur 8 mK, in doppelt-logarithmischer Darstellung.
Für Frequenzen F < 10⁷Hz zeigt sich in diesem Beispiel eine gute Übereinstimmung der Vorhersagen nach Rayleigh-Jeans und Planck, danach weicht Rayleigh-Jeans zunehmend stark nach oben ab. Wien hingegen beschreibt den Grenzfall hoher Frequenzen (hier $F > 4\times {10^8}\, \mathrm{Hz}$) sehr gut, liegt aber für geringere Frequenzen deutlich zu niedrig.

Das Rayleigh-Jeans-Gesetz beschreibt die Abhängigkeit der Strahlungsintensität eines Schwarzen Körpers von der Lichtwellenlänge bei einer gegebenen Temperatur im Rahmen der klassischen Elektrodynamik. Es wurde erstmals 1900 von dem englischen Physiker John William Strutt, 3. Baron Rayleigh beschrieben^[1], wobei die von Rayleigh beschriebene Formel noch einen falschen Vorfaktor aufwies. Die korrekte Formel wurde fünf Jahre später von dem englischen Physiker, Astronom und Mathematiker Sir James Jeans veröffentlicht^[2].

Das Rayleigh-Jeans-Gesetz liefert brauchbare Werte bei niedrigen Frequenzen, also großen Wellenlängen, siehe Bild. Bei kleinen Wellenlängen liefert es viel zu große Werte, die die Gesamtstrahlung, integriert über den gesamten Wellenlängenbereich, gegen unendlich streben lassen. Das Verhalten wurde als Ultraviolett-Katastrophe bezeichnet^[3]. Das Verhalten bei kleinen Wellenlängen, also hohen Frequenzen (und damit entsprechend hoher Energie), wird in guter Näherung durch das wiensche Strahlungsgesetz beschrieben.

Erst Max Planck fand die richtige Erklärung und fasste mit dem planckschen Strahlungsgesetz das Rayleigh-Jeans-Gesetz und das wiensche Strahlungsgesetz zusammen.

Wählt man $hc/\lambda \ll kT$, folgt aus dem planckschen Strahlungsgesetz

$I(\lambda) \, \mathrm{d}\lambda = \frac{2 \pi h c^2} {\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}\mathrm{d} \lambda\ .$

unter der Näherung von $e^x \approx 1+x$ für kleine Exponenten unmittelbar das Rayleigh-Jeans-Gesetz:

$I(\lambda) \, \mathrm{d}\lambda = \frac{2 \pi c k T} {\lambda^4}\mathrm{d} \lambda .$

Einzelnachweise

1. ↑ L. Rayleigh: Remarks upon the Law of Complete Radiation. In: Phil. Mag.. 49, 1900, S. 539–540.
2. ↑ J. H. Jeans: On the partition of energy between matter and Aether. In: Phil. Mag.. 10, 1905, S. 91–98.
3. ↑ Die physikalisch unsinnige Divergenz des Rayleigh-Jeans-Gesetzes bei hohen Strahlungsfrequenzen wurde erstmals im Jahr 1905 (unabhängig voneinander) von Einstein, Rayleigh und Jeans beschrieben. Der Begriff Ultraviolett-Katastrophe wurde erstmals 1911 von Paul Ehrenfest verwendet.
   P. Ehrenfest: Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?. In: Annalen der Physik. 341, Nr. 11, 1911, S. 91–118.