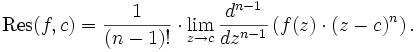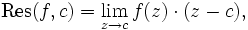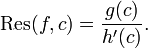- Residuenkalkül
-
Zum Residuenkalkül - ein Begriff aus der Mathematik - gehört die konkrete Berechnung von Residuen (siehe Laurent-Reihe) meromorpher Funktionen sowie die Auswertung von Integralen über geschlossene Kurven in den komplexen Zahlen mit Hilfe des Residuensatzes. Die praktisch wichtigste Formel zur Auswertung des Residuums einer Funktion mit n-facher Polstelle am Punkt
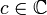 lautet:
lautet:Für den oft auftretenden Fall des einfachen Pols vereinfacht sich die Formel zu
Für Funktionen der Gestalt
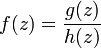 , wobei g holomorph und c eine einfache Nullstelle von h sei:
, wobei g holomorph und c eine einfache Nullstelle von h sei:Uneigentliche Integrale
Für Funktionen, deren Betrag in der oberen oder unteren Halbebene für große z und ein beliebiges
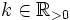 schneller als k | z | − 1 fällt, steht nun eine weitere Möglichkeit zur Verfügung, uneigentliche Integrale über die reelle Achse auszuwerten. Dazu schließt man die Integrationskontur mit Hilfe eines Halbkreises in der passenden Halbebene, dessen Radius man gegen unendlich gehen lässt. Das Integral über die geschlossene Kontur wertet man mit Hilfe des Residuensatzes aus. Der Betrag des Integrals über den Halbkreis verschwindet nun, da die Funktion ausreichend schnell fällt, um die Vergrößerung des Integrationsgebiets auszugleichen. Der mit Hilfe des Residuensatzes ausgerechnete Wert ist also gleich dem Integral über
schneller als k | z | − 1 fällt, steht nun eine weitere Möglichkeit zur Verfügung, uneigentliche Integrale über die reelle Achse auszuwerten. Dazu schließt man die Integrationskontur mit Hilfe eines Halbkreises in der passenden Halbebene, dessen Radius man gegen unendlich gehen lässt. Das Integral über die geschlossene Kontur wertet man mit Hilfe des Residuensatzes aus. Der Betrag des Integrals über den Halbkreis verschwindet nun, da die Funktion ausreichend schnell fällt, um die Vergrößerung des Integrationsgebiets auszugleichen. Der mit Hilfe des Residuensatzes ausgerechnete Wert ist also gleich dem Integral über  .
.Literatur
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3. Auflage. Springer-Verlag Berlin Heidelberg, 2000
Wikimedia Foundation.