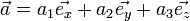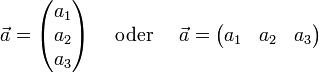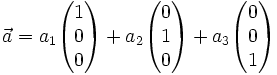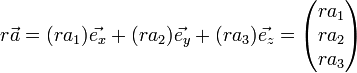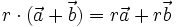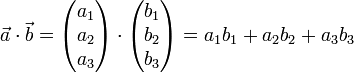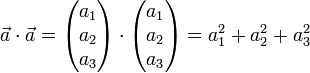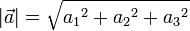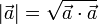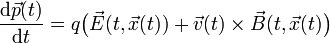- Richtungsvektor
-
Ein Vektor (lat. vector „jemand, der trägt, zieht oder befördert“; zu lat. vehere = fahren) ist in der Mathematik ein Element eines Vektorraums. Das bedeutet unter anderem, dass sich beliebige zwei Vektoren durch Addition zu einem dritten Vektor des gleichen Vektorraums verknüpfen lassen. Eine Multiplikation zwischen Vektoren kann definiert sein, muss aber nicht.
Damit ist der mathematische Begriff eine Verallgemeinerung der in der Physik benutzten geometrischen Vorstellung eines Vektors als Pfeil mit den Eigenschaften Länge und Richtung. Die Länge des Pfeils entspricht dabei dem Betrag des Vektors. Beispiele sind die Geschwindigkeit oder der Impuls als Größen im dreidimensionalen Raum.
Inhaltsverzeichnis
Geometrie
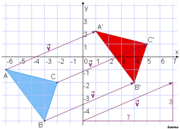
Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um 7 Einheiten nach rechts und 3 nach oben verschoben werden. Er bewegt sich dabei längs eines Pfeils
 . Da diese Pfeile in Länge, Richtung und Orientierung übereinstimmen, fasst man sie zu einer Klasse (Vektorklasse) zusammen, die man ebenfalls kurz mit
. Da diese Pfeile in Länge, Richtung und Orientierung übereinstimmen, fasst man sie zu einer Klasse (Vektorklasse) zusammen, die man ebenfalls kurz mit  bezeichnet. Jeder Pfeil ist ein Repräsentant dieser Klasse. Man beschreibt die Klasse durch die Verschiebung, die ihre Pfeile bewirken, im Beispiel:
bezeichnet. Jeder Pfeil ist ein Repräsentant dieser Klasse. Man beschreibt die Klasse durch die Verschiebung, die ihre Pfeile bewirken, im Beispiel: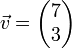 ,
,
im dreidimensionalen Raum entsprechend mit 3 Komponenten, siehe weiter unten und Hauptartikel: Parallelverschiebung.
Die Definition des Vektors in der linearen Algebra als Element eines Vektorraumes ist eine viel umfassendere, die neben den „herkömmlichen“, geometrischen Vektoren verschiedenste mathematische Objekte (Zahlen, Folgen, Funktionen und Transformationen) beinhaltet. Demnach ist auch jeder Vektor ein Tensor. Auch alle benannten Größen – wie Längenangaben in Meter, Geldbeträge usw. – sind in diesem Sinn Vektoren.
In der Differentialgeometrie, der Physik und der Technik bezieht sich der Ausdruck Vektor normalerweise auf einen geometrischen Vektor des euklidischen Raumes, der durch einen Betrag, eine Richtung und eine Orientierung gegeben ist. Beispiele sind Geschwindigkeit, Impuls, Kraft, Moment und Beschleunigung. Nach dieser Definition ist ein Vektor ein Tensor erster Stufe. Alle folgenden Betrachtungen beziehen sich auf solche Vektoren, allgemeine Eigenschaften finden sich unter Vektorraum.
Vektoren kann man skalaren Größen wie Abstand, Energie, Ladung, Arbeit oder Masse gegenüberstellen, die zwar einen Betrag, aber keine Richtung und keine Orientierung haben.
Vektoren sind normalerweise ungebunden, das heißt, sie haben keinen fixen Ausgangspunkt. Ein Vektor kann daher als die Menge aller „Pfeile“, die kollinear (d. h. parallel sind, also die gleiche Richtung besitzen), gleich lang und gleich orientiert sind, angesehen werden. Sie dienen im Allgemeinen dazu, eine Richtung anzuzeigen und heißen dann Richtungsvektor.
Im Unterschied dazu haben gebundene Vektoren einen Ursprung (Ausgangspunkt). Sie können zum Beispiel, als so genannte Ortsvektoren, die Position eines Punktes im Raum angeben. Kräfte, die auf Starrkörper wirken, sind teilweise gebunden. Sie wirken entlang einer bestimmten Geraden. Es ist egal, an welchem Punkt der Geraden sie angreifen. Man nennt sie „linienflüchtige“ Vektoren.
Ein Vektor mit der Länge 1 heißt Einheitsvektor. Man kann jeden Vektor mit Ausnahme des Nullvektors zu einem Einheitsvektor machen, indem man ihn normiert, das heißt alle Koordinaten durch den Betrag (die Länge) des Vektors teilt.
Ein Vektor mit gleichem Betrag, gleicher Richtung aber entgegengesetzter Orientierung eines anderen Vektors ist dessen Gegenvektor.
Darstellungsformen
Variablen, die für Vektoren stehen, werden vor allem in der Schulmathematik und in der Physik häufig mit einem Pfeil gekennzeichnet (
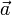 ) oder, vor allem im englischsprachigen Raum, fett geschrieben (a). In englischen Handschriften wird dies häufig durch Unterstreichung (
) oder, vor allem im englischsprachigen Raum, fett geschrieben (a). In englischen Handschriften wird dies häufig durch Unterstreichung (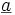 ) oder ähnliches repräsentiert. Wie alle Variablen werden auch Vektoren allgemein kursiv gesetzt, unabhängig davon, ob sie fett (englisch) oder mit Pfeil (deutsch) gekennzeichnet sind. Früher war teilweise auch die Schreibweise mit Frakturbuchstaben (
) oder ähnliches repräsentiert. Wie alle Variablen werden auch Vektoren allgemein kursiv gesetzt, unabhängig davon, ob sie fett (englisch) oder mit Pfeil (deutsch) gekennzeichnet sind. Früher war teilweise auch die Schreibweise mit Frakturbuchstaben (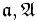 ) üblich. (Anmerkung: In diesem Artikel wird durchgängig die Pfeilschreibweise verwendet, in anderen Wikipedia-Artikeln kommt aber auch der Fettdruck vor.) Ist der Betrag, also die Länge des Vektors gemeint, wird der Vektor mit zwei senkrechten Betragsstrichen eingeklammert:
) üblich. (Anmerkung: In diesem Artikel wird durchgängig die Pfeilschreibweise verwendet, in anderen Wikipedia-Artikeln kommt aber auch der Fettdruck vor.) Ist der Betrag, also die Länge des Vektors gemeint, wird der Vektor mit zwei senkrechten Betragsstrichen eingeklammert: 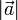
Vektoren werden häufig als Pfeile dargestellt:
A wird in diesem Fall als Ausgangs- oder Startpunkt und B als Spitze oder Endpunkt des Vektors bezeichnet. Die Lage der Pfeilspitze gibt die Orientierung des Vektors, die Länge seinen Betrag und der Pfeilschaft seine Richtung an. Dieser Vektor kann auch als
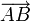 bezeichnet werden und sein Betrag als
bezeichnet werden und sein Betrag als 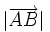 bzw.
bzw. 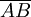 . Dabei ist zu beachten, dass der Vektor nicht an die Punkte A und B gebunden ist, sondern dass diese ihn nur definieren.
. Dabei ist zu beachten, dass der Vektor nicht an die Punkte A und B gebunden ist, sondern dass diese ihn nur definieren.Um mit Vektoren sinnvoll rechnen zu können, ist die grafische Notation natürlich unpraktisch. In einem n-dimensionalem Euklidischen Raum können Vektoren als Linearkombination von n Basisvektoren dieses Raumes dargestellt werden. Im kartesischen Koordinatensystem nimmt man dafür n paarweise aufeinander normal stehende Einheitsvektoren.
Als Beispiel für diesen Artikel soll immer der dreidimensionale Vektorraum
 mit einem kartesischen Koordinatensystem dienen. Sind
mit einem kartesischen Koordinatensystem dienen. Sind 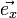 ,
, 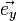 und
und 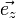 die Einheitsvektoren in Richtung der x-, y- bzw. z-Achse, kann jeder Vektor als
die Einheitsvektoren in Richtung der x-, y- bzw. z-Achse, kann jeder Vektor alsangeschrieben werden. Die reellen Zahlen a1, a2 und a3 sind eindeutig durch
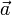 festgelegt. Oft schreibt man Vektoren auch kurz als 3×1- oder 1×3-Matrix und nennt sie stehende oder liegende Vektoren:
festgelegt. Oft schreibt man Vektoren auch kurz als 3×1- oder 1×3-Matrix und nennt sie stehende oder liegende Vektoren:Mit dieser Schreibweise ist zwar die Wahl des Koordinatensystems nicht festgehalten, falls nichts anderes angegeben ist aber immer das kartesische Koordinatensystem gemeint, da es für viele Rechnungen am einfachsten ist.
Man kann dann die Koordinaten eines Vektor auch so darstellen:
Rechenoperationen
Addition und Subtraktion
Die Summe der beiden Vektoren
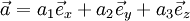 und
und 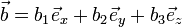
berechnet sich als:
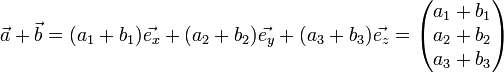 .
.
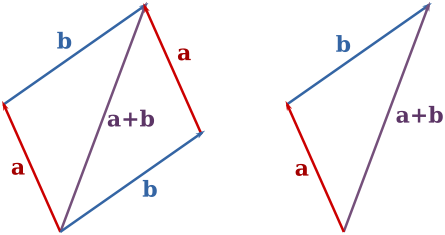
Die Vektoraddition kann man graphisch interpretieren, indem man den Startpunkt des zweiten Vektors mittels Parallelverschiebung auf den Endpunkt des ersten Vektors verschiebt. Der Pfeil vom Startpunkt des ersten Vektors bis zum Endpunkt des zweiten Vektors repräsentiert den Ergebnisvektor:
Aus je zwei Vektoren
 und
und  lässt sich ein Parallelogramm bilden, dessen eine Diagonale der Summe beider Vektoren entspricht. In der Physik verwendet man diese Konstruktion beim Kräfteparallelogramm.
lässt sich ein Parallelogramm bilden, dessen eine Diagonale der Summe beider Vektoren entspricht. In der Physik verwendet man diese Konstruktion beim Kräfteparallelogramm.Für die Addition von Vektoren gilt das Assoziativgesetz und das Kommutativgesetz.
Die Differenz dieser beiden Vektoren ist:
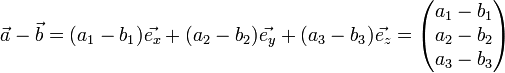 .
.
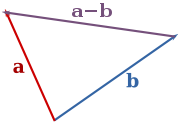
Die geometrische Interpretation der Subtraktion von zwei Vektoren ist: Zwei Vektoren werden subtrahiert, indem man den Startpunkt des Gegenvektors des zweiten Vektors an den Endpunkt des ersten Vektors anschließt. Geometrisch entspricht die Differenz dem Verbindungsvektor zwischen den Endpunkten des zweiten und des ersten Vektors.
Multiplikation mit einem Skalar
Vektoren können mit reellen Zahlen (oft Skalare genannt, um sie von Vektoren unterscheiden zu können) multipliziert werden (Skalarmultiplikation, auch S-Multiplikation genannt):
Die Länge des resultierenden Vektors ist daher
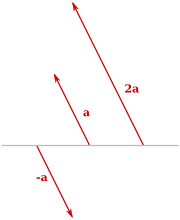
 . Wenn der Skalar positiv ist, zeigt der resultierende Vektor in dieselbe Richtung, ist er negativ, in die Gegenrichtung. Die folgende Grafik illustriert zwei Beispiele (Multiplikation mit −1 und 2):Wobei der Vektor auch die Richtung ändern kann x(−1)
. Wenn der Skalar positiv ist, zeigt der resultierende Vektor in dieselbe Richtung, ist er negativ, in die Gegenrichtung. Die folgende Grafik illustriert zwei Beispiele (Multiplikation mit −1 und 2):Wobei der Vektor auch die Richtung ändern kann x(−1)Für die Vektoraddition und die Multiplikation mit einem Skalar gilt das Distributivgesetz:
Die Multiplikation eines Vektors mit einem Skalar wird häufig auch S-Multiplikation genannt.
Skalarprodukt
Hauptartikel: Skalarprodukt
Das Skalarprodukt (oder inneres Produkt) zweier Vektoren
 und
und  , so genannt weil das Ergebnis ein Skalar ist, wird notiert als
, so genannt weil das Ergebnis ein Skalar ist, wird notiert als 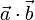 oder
oder 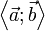 und ist
und ist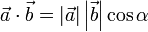 ,
,
wobei α der zwischen den beiden Vektoren eingeschlossene Winkel ist (siehe auch Kosinus). Stehen die zwei Vektoren rechtwinkelig zueinander, so ist das Skalarprodukt Null:
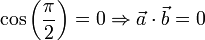 .
.Im kartesischen Koordinatensystem berechnet sich das Skalarprodukt als
insbesondere gilt für das Quadrat eines Vektors
Geometrisch lässt sich das Skalarprodukt auch als Multiplikation der Länge des ersten Vektors mit der Länge der senkrechten Projektion des zweiten Vektors auf den ersten Vektor verstehen. Daher ist das Skalarprodukt zweier orthogonal aufeinander stehender Vektoren immer 0. Diese Operation wird oft in der Physik gebraucht, zum Beispiel um die Arbeit zu berechnen, wenn Kraft und Weg nicht in derselben Richtung verlaufen.
Für das Skalarprodukt gelten das Kommutativgesetz und das Distributivgesetz, nicht aber - wie bei der Multiplikation zweier Skalare - das Assoziativgesetz.
Kreuzprodukt
Hauptartikel: Kreuzprodukt
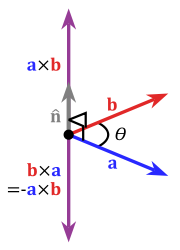
Das Kreuzprodukt (auch vektorielles Produkt, äußeres Produkt oder Vektorprodukt)
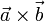 (gesprochen als „a Kreuz b“) zweier Vektoren in einem dreidimensionalen euklidischen Vektorraum ist ein bestimmter Vektor, der normal (senkrecht im Sinne des Skalarprodukts) auf der von
(gesprochen als „a Kreuz b“) zweier Vektoren in einem dreidimensionalen euklidischen Vektorraum ist ein bestimmter Vektor, der normal (senkrecht im Sinne des Skalarprodukts) auf der von  und
und  aufgespannten Ebene steht. Die Länge dieses Vektors entspricht der Fläche des Parallelogramms mit den Seiten
aufgespannten Ebene steht. Die Länge dieses Vektors entspricht der Fläche des Parallelogramms mit den Seiten  und
und  .
.Betrag eines Vektors
Im dreidimensionalen euklidischen Raum kann die Länge oder der Betrag nach dem Satz des Pythagoras berechnet werden:
Dieser Betrag oder Länge kann durch das Skalarprodukt ausgedrückt werden:
Die Länge oder der Betrag ordnet jedem Vektor eine nicht negative Zahl zu. Vektorräume mit einer solchen Zuordnung, die bestimmte Axiome erfüllt, heißen in der Mathematik normierte Räume. Eine Norm kann immer wie oben angegeben mit der Wurzel des Skalarprodukts definiert werden, falls das Skalarprodukt in dem Vektorraum definiert ist.
Vektoren in der Physik
In der Physik sind mit Vektoren häufig Vektoren eines drei- oder vierdimensionalen Vektorraumes gemeint. Zum Beispiel werden der Ort, die Geschwindigkeit, der Impuls, die Beschleunigung, die Kraft, die Winkelgeschwindigkeit, der Drehimpuls, die elektrische und die magnetische Feldstärke durch Vektoren in dreidimensionalen Räumen angegeben. Ein Ereignis, die Vierergeschwindigkeit, die Viererbeschleunigung und der Viererimpuls werden durch vierdimensionale Vektoren angegeben.
Für den physikalischen Vektorbegriff ist auch das Transformationsverhalten unter der Isometriegruppe der entsprechenden Metrik von Bedeutung. Dabei wird der dreidimensionale Raum als euklidischer Raum verstanden, während die vierdimensionale Raumzeit als Minkowskiraum mit der entsprechenden Metrik aufgefasst wird. Werden diese Räume als Mannigfaltigkeiten aufgefasst, so sind Vektoren als kontravariante Tensoren erster Stufe zu verstehen, was das geforderte Transformationsverhalten festlegt. Die zugehörigen Isometriegruppen sind in drei Dimensionen die Drehgruppe und im Minkowskiraum die Lorentzgruppe. Dabei sind nicht alle Vektoren im Dreidimensionalen als Teile von Vierervektoren aufzufassen. Der Drehimpuls transformiert beispielsweise unter Lorentztransformationen nicht wie ein Teil eines Vierervektors, sondern zusammen mit dem anfänglichen Energieschwerpunkt wie die sechs Komponenten eines antisymmetrischen Tensors. Ebenso transformieren die elektrische und magnetische Feldstärke wie die sechs Komponenten eines antisymmetrischen Tensors.
Vielteilchensysteme mit n Teilchen beschreibt man mit Vektoren in 3-n-dimensionalen Vektorräumen auf die die dreidimensionale Drehgruppe getrennt wirkt.
Unterscheiden sich die Maßeinheiten zweier Vektoren, so ist ihre Addition nicht definiert: Sie sind Elemente verschiedener Räume, auch wenn sie sich auf gleiche Art drehen oder unter orientierungstreuen Lorentztransformationen verändern.
Je nach Transformationsverhalten unter Spiegelungen des Ortes unterscheidet man zwischen polaren Vektoren und axialen Vektoren: In polaren Vektorräumen geht jeder Vektor bei der räumlichen Spiegelung in sein negatives über, Axialvektoren bleiben dabei unverändert. So ändern beispielsweise der Ort, die Geschwindigkeit, der Impuls und das elektrische Feld bei räumlicher Spiegelung ihr Vorzeichen, nicht aber das magnetische Feld. Bei solchen Transformationen gehen Lösungen
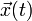 der Bewegungsgleichungen im elektromagnetischen Feldern
der Bewegungsgleichungen im elektromagnetischen Feldernbei Spiegelung in Lösungen der Bewegungsgleichungen in transformierten elektromagnetischen Feldern über.
Polare und axiale Vektoren sind wegen ihres unterschiedlichen Transformationsverhaltens Elemente verschiedener Vektorräume. Das Kreuzprodukt muss dabei als bilineare Abbildung zweier Vektorräume in einen dritten angesehen werden. Dass es sich um verschiedene Vektorräume handelt, ist meist schon an den Maßeinheiten sichtbar.
Geschichte
Begründet wurde die Vektorrechnung von Hermann Günter Graßmann, der 1844 seine Lineale Ausdehnungslehre veröffentlichte, ein über dreihundert Seiten starkes Buch.[1] Als Vorläufer gelten u. a. René Descartes und August Ferdinand Möbius, ein Schüler von Carl Friedrich Gauß. Nahezu zeitgleich entwickelte William Rowan Hamilton seine ähnliche Theorie [2] der Quaternionen, die er 1853 in dem Buch Lectures on Quaternions[3] und 1866 in dem Werk Elements of Quaternions[4][5] publizierte. In Deutschland wurde die Vektorrechnung insbesondere durch Vorlesungen und Bücher z. B. von Alfred Bucherer, August Föppl, Carl Runge, Fischer, v. Ignatowsky und Richard Gans verbreitet.
Literatur
- Kurt Bohner, Peter Ihlenburg, Roland Ott: Mathematik für berufliche Gymnasien – Lineare Algebra Vektorielle Geometrie. Merkur, Rinteln 2004, ISBN 3-8120-0552-2.
- Klaus Jänich: Lineare Algebra. 10. Auflage. Springer, Berlin 2004, ISBN 3-540-40207-1.
- Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 1. 11. Auflage, Vieweg, Wiesbaden 2007, ISBN 978-3-8348-0224-8.
Weblinks
- Vektorrechnung, Ronny Harbich
- Javaapplet zur Veranschaulichung der Vektoraddition
- Javaapplet zur Veranschaulichung des Kreuzprodukts
- Der mathematische Begriff „Vektor“
- mathe online: Vektoren
- Geschichte des Vektors (englisch)
Einzelnachweise
- ↑ Hermann Günter Graßmann: Die Lineale Ausdehnungslehre ein neuer Zweig der Mathematik: Dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert. O. Wigand, 1844.
- ↑ Josiah Willard Gibbs: Quaternions and the Ausdehnungslehre»Sammelwerk=Nature. 44, Nr. 1126, 1891, S. 79-82 (doi:10.1038/044079b0).
- ↑ W. R. Hamilton: Lectures on Quaternions. Hodges and Smith, Dublin 1853.
- ↑ W. R. S. Hamilton: Elements of Quaternions: Vol.: 1. Longmans, Green & Company, 1866 (Google Books).
- ↑ W. R. S. Hamilton, C. J. Joly: Elements of quaternions.Vol.: 2. Longmans, Green & Company, 1901.
Wikimedia Foundation.