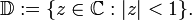- Riemannsche Abbildungssatz
-
Der (kleine) riemannsche Abbildungssatz (nach Bernhard Riemann) aus dem Jahr 1851 ist ein Satz der Funktionentheorie und besagt:
Jedes einfach zusammenhängende Gebiet G, das eine echte (offene) Teilmenge der komplexen Zahlenebene
 ist, lässt sich biholomorph auf die offene Einheitskreisscheibe
ist, lässt sich biholomorph auf die offene Einheitskreisscheibe 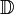 abbilden.
abbilden.Zur Klärung der in diesem Satz verwendeten Begriffe:
Die offene Einheitskreisscheibe
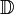 ist definiert als
ist definiert alsBereiche sind nichtleere offene Mengen in
 .
.Zusammenhängende Bereiche von
 werden als Gebiete bezeichnet.
werden als Gebiete bezeichnet.„Echte Teilmenge“ besagt, dass das Gebiet G ungleich
 sein muss.
sein muss.Eine offene Menge in
 kann man dadurch charakterisieren, dass jeden ihrer Punkte eine Kreisscheibe umgibt, die ganz in dieser Menge liegt; mit anderen Worten, dass sie nur aus inneren Punkten besteht.
kann man dadurch charakterisieren, dass jeden ihrer Punkte eine Kreisscheibe umgibt, die ganz in dieser Menge liegt; mit anderen Worten, dass sie nur aus inneren Punkten besteht.Eine offene Menge ist zusammenhängend, wenn sie nicht als disjunkte Vereinigung zweier offener Mengen geschrieben werden kann. Eine offene Menge ist wegzusammenhängend, wenn es von jedem Punkt zu jedem anderen einen stetigen Weg gibt. Für offene Teilmengen von
 stimmen die Begriffe zusammenhängend und wegzusammenhängend überein. Eine wegzusammenhängende Menge heißt einfach zusammenhängend, wenn jede Schleife (ein Weg, dessen Start- auch der Endpunkt ist) auf einen Punkt zusammengezogen werden kann, d. h., die Menge „hat keine Löcher“. Einfach zusammenhängende offene Teilmengen von
stimmen die Begriffe zusammenhängend und wegzusammenhängend überein. Eine wegzusammenhängende Menge heißt einfach zusammenhängend, wenn jede Schleife (ein Weg, dessen Start- auch der Endpunkt ist) auf einen Punkt zusammengezogen werden kann, d. h., die Menge „hat keine Löcher“. Einfach zusammenhängende offene Teilmengen von  sind zusammenziehbar. Siehe auch Zusammenhang (Topologie) und Fundamentalgruppe.
sind zusammenziehbar. Siehe auch Zusammenhang (Topologie) und Fundamentalgruppe.Eine Abbildung ist biholomorph, wenn sie holomorph ist und wenn ihre Umkehrabbildung existiert und diese ebenfalls holomorph ist. Insbesondere sind solche Abbildungen Homöomorphismen, also in beide Richtungen stetig. Hieraus und unter Verwendung des riemannschen Abbildungssatzes kann man schließen, dass alle einfach zusammenhängenden Gebiete, die echte Teilmengen von
 sind, topologisch äquivalent sind.
sind, topologisch äquivalent sind.Für jeden Punkt z des einfach zusammenhängenden Gebietes G gilt: Es gibt genau eine biholomorphe Funktion h von G auf
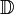 mit h(z) = 0 und h'(z) > 0.
mit h(z) = 0 und h'(z) > 0.Alternativ lässt sich die obenstehende Aussage auch so formulieren: Zu frei wählbaren Punkten z aus G, s aus dem Rand von G und t aus dem Rand von
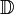 gibt es genau eine biholomorphe Funktion h von G auf
gibt es genau eine biholomorphe Funktion h von G auf 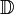 mit h(z) = 0 und h(s) = t.
mit h(z) = 0 und h(s) = t.Riemann skizzierte einen Beweis 1851 in seiner Dissertation. 1922 wurde er dann endgültig durch Lipot Fejer und Frigyes Riesz bewiesen.
Ein heute weit verbreiteter Beweis (der mit dem Satz von Montel erfolgt) stammt von Alexander Markowitsch Ostrowski aus dem Jahre 1929.
Großer riemannscher Abbildungssatz
Der große riemannsche Abbildungssatz, auch als Uniformisierungssatz bezeichnet, ist eine Verallgemeinerung des oben genannten Satzes. Er besagt:
- Jede einfach zusammenhängende riemannsche Fläche ist biholomorph äquivalent zu genau einer der folgenden Flächen:
- der Einheitskreisscheibe
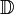 , bzw. zur dazu äquivalenten hyperbolischen Halbebene
, bzw. zur dazu äquivalenten hyperbolischen Halbebene 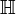 ,
, - der komplexen Zahlenebene
 oder
oder - der riemannschen Zahlenkugel
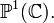
- der Einheitskreisscheibe
Anmerkung: Es ist vergleichsweise einfach, zu erkennen, dass die drei genannten Riemannschen Flächen paarweise nicht biholomorph äquivalent sind: Eine biholomorphe Abbildung von
 nach
nach 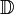 ist nach dem Satz von Liouville nicht möglich und die Zahlenkugel ist kompakt und ist somit schon aus rein topologischen Gründen nicht homöomorph (also erst recht nicht biholomorph äquivalent) zu
ist nach dem Satz von Liouville nicht möglich und die Zahlenkugel ist kompakt und ist somit schon aus rein topologischen Gründen nicht homöomorph (also erst recht nicht biholomorph äquivalent) zu 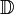 oder
oder  .
.
Wikimedia Foundation.