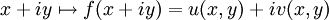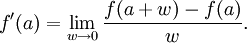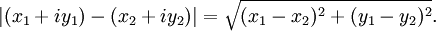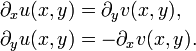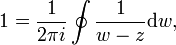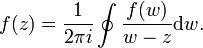- Komplexe Analysis
-
Die Funktionentheorie ist ein Teilgebiet der Mathematik. Sie befasst sich mit den differenzierbaren komplexwertigen Funktionen komplexer Variablen. Gebräuchlich ist auch die Bezeichnung komplexe Analysis.
Komplexe Funktionen
Eine komplexe Funktion ordnet einer komplexen Zahl eine weitere komplexe Zahl zu. Da jede komplexe Zahl durch zwei reelle Zahlen in der Form x + iy geschrieben werden kann, lässt sich eine allgemeine Form einer komplexen Funktion durch
darstellen. Hier sind
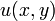 und
und 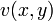 reelle Funktionen, die von zwei reellen Variablen x und y abhängen.
reelle Funktionen, die von zwei reellen Variablen x und y abhängen. 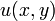 heißt der Realteil und
heißt der Realteil und 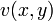 der Imaginärteil der Funktion. Insofern ist eine komplexe Funktion eine spezielle reelle Abbildung von
der Imaginärteil der Funktion. Insofern ist eine komplexe Funktion eine spezielle reelle Abbildung von 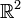 nach
nach 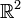 (also eine Abbildung, die zwei reellen Zahlen wieder zwei reelle Zahlen zuordnet). Tatsächlich könnte man die ganze Funktionentheorie auch mit reeller Analysis behandeln. Der Unterschied zur reellen Analysis wird erst deutlicher, wenn man komplex-differenzierbare Funktionen betrachtet.
(also eine Abbildung, die zwei reellen Zahlen wieder zwei reelle Zahlen zuordnet). Tatsächlich könnte man die ganze Funktionentheorie auch mit reeller Analysis behandeln. Der Unterschied zur reellen Analysis wird erst deutlicher, wenn man komplex-differenzierbare Funktionen betrachtet.Funktionen mehrerer komplexer Variablen
Es gibt auch komplexwertige Funktionen mehrerer komplexer Variablen. Im Vergleich zur reellen Analysis gibt es in der komplexen Analysis fundamentale Unterschiede zwischen Funktionen einer und mehrerer Variablen. Beispielsweise besitzen holomorphe Funktionen mehrerer Variablen keine isolierten Singularitäten, was aus dem sog. Kugelsatz von Hartogs folgt, und als Konsequenz auch keine isolierten Nullstellen. Auch der riemannsche Abbildungssatz - ein Höhepunkt der Funktionentheorie in einer Variablen - hat kein Äquivalent in höheren Dimensionen. Nicht einmal die beiden natürlichen Verallgemeinerungen der eindimensionalen Kreisscheibe, Einheitskugel und Polyzylinder, sind in mehreren Dimensionen biholomorph äquivalent. Ein großer Teil der Funktionentheorie mehrerer Variablen beschäftigt sich mit Fortsetzungsphänomenen (riemannsche Hebbarkeitssätze, Kugelsatz von Hartogs, Satz von Bochner über Röhrengebiete, Cartan-Thullen-Theorie). Eine gute Einführung in die Funktionentheorie mehrerer Variablen gibt das Buch von Freitag/Busam oder auch das von Scheidemann (siehe Literaturverzeichnis). Die Funktionentheorie mehrerer komplexer Variablen wird zum Beispiel in der Quantenfeldtheorie benutzt.
Komplexe Differenzierbarkeit
Hauptartikel: Holomorphie
Der Differenzierbarkeitsbegriff der eindimensionalen reellen Analysis wird in der Funktionentheorie zur komplexen Differenzierbarkeit erweitert. Analog zum reellen Fall definiert man: Eine Funktion einer komplexen Variablen heißt komplex-differenzierbar, falls der folgende Grenzwert existiert:
Für eine exakte Definition muss f dabei in einer Umgebung von a definiert sein. Für den Grenzwert muss dabei der komplexe Abstandsbegriff verwendet werden:
Damit sind für komplexwertige Funktionen einer komplexen Variablen zwei verschiedene Differenzierbarkeitsbegriffe definiert: die komplexe Differenzierbarkeit und die Differenzierbarkeit der zweidimensionalen reellen Analysis (reelle Differenzierbarkeit). Komplex-differenzierbare Funktionen sind auch reell-differenzierbar, die Umkehrung gilt nicht ohne zusätzliche Voraussetzungen.
Cauchy-Riemannsche Differentialgleichungen
Hauptartikel: Cauchy-Riemannsche Differentialgleichungen
Äquivalent zur komplexen Differenzierbarkeit sind die Forderungen an die reellen partiellen Ableitungen der Funktion:
Die Rückrichtung folgt nur, wenn die partiellen Ableitungen im ganzen Gebiet stetig sind.
Cauchysche Integralformel
Hauptartikel: Cauchysche Integralformel
Mit einem Integrationsweg, der keinerlei Singularitäten von f umläuft und für dessen Umlaufzahl um z gilt, dass
gilt die cauchysche Integralformel:
Diese besagt, dass der Wert einer komplex-differenzierbaren Funktion auf einem Gebiet nur von den Funktionswerten auf dem Rand des Gebiets abhängt.
Holomorphe Funktionen
Funktionen, die in einer Umgebung eines Punktes komplex-differenzierbar sind, nennt man holomorphe oder analytische Funktionen. Diese haben eine Reihe hervorragender Eigenschaften, die es rechtfertigen, dass sich eine eigene Theorie hauptsächlich damit beschäftigt - eben die Funktionentheorie. Zum Beispiel ist eine Funktion, die einmal komplex-differenzierbar ist, automatisch beliebig oft komplex-differenzierbar (im Gegensatz zum reellen Fall).
Äquivalente Definitionen holomorpher Funktionen einer Variablen
In einer Umgebung einer komplexen Zahl sind folgende Eigenschaften komplexer Funktionen gleichwertig:
- Eine Funktion ist einmal komplex-differenzierbar
- Eine Funktion ist beliebig oft komplex-differenzierbar
- Real- und Imaginärteil erfüllen die cauchy-riemannschen Differentialgleichungen und sind zumindest einmal stetig reell-differenzierbar
- Die Funktion lässt sich in eine komplexe Potenzreihe entwickeln
- Das Wegintegral der Funktion über einen beliebigen geschlossenen zusammenziehbaren Weg verschwindet.
- Die Funktionswerte im Inneren einer Kreisscheibe lassen sich aus den Funktionswerten am Rand mit Hilfe der cauchyschen Integralformel ermitteln.
- Es gilt
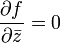 mit
mit 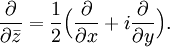
Holomorphe Funktionen sind somit sehr "angenehme" Funktionen: Sie sind beliebig oft komplex-differenzierbar, können in eine Potenzreihe (Taylor-Reihe) entwickelt werden und vieles mehr. Fast alle Funktionen, die aus der Schulmathematik bekannt sind, sind Real- oder Imaginärteil einer holomorphen Funktion (zumindest auf einem Teil der komplexen Ebene): Insbesondere gilt das für Polynome, rationale Funktionen, trigonometrische Funktionen (Sinus, Kosinus), Exponentialfunktion, Logarithmus, und Wurzelfunktionen.
Meromorphe Funktionen
Meromorphe Funktionen sind bis auf isolierte Polstellen holomorph. Sie lassen sich in Laurentreihen entwickeln, die nur endlich viele Reihenglieder mit negativen Potenzen der Variablen z = x + iy besitzen, bzw. nur endlich viele Glieder mit negativen Potenzen von z − a in der Umgebung einer Polstelle a.
Funktionen mit wesentlichen Singularitäten
Neben holomorphen und meromorphen Funktionen gibt es in der Funktionentheorie Funktionen mit wesentlichen Singularitäten. Sie sind dadurch charakterisiert, dass eine Funktion in jeder Umgebung einer wesentlichen Singularität jeden beliebigen komplexen Zahlenwert mit höchstens einer Ausnahme annimmt (Satz von Picard). Funktionen mit wesentlichen Singularitäten haben dort nicht abbrechende Laurententwicklungen der Potenzen mit negativen Exponenten.
Funktionentheoretische Methoden in anderen mathematischen Teilgebieten
Eine klassische Anwendung der Funktionentheorie liegt in der Zahlentheorie. Benutzt man dort funktionentheoretische Methoden, nennt man dieses Gebiet dann analytische Zahlentheorie. Wichtige Ergebnisse sind beispielsweise der Primzahlsatz.
Reelle Funktionen, die sich in eine Potenzreihe entwickeln lassen, sind auch Realteil einer holomorphen Funktion. Damit lassen sich diese Funktionen auf die komplexe Ebene erweitern. Durch diese Erweiterung kann man oft Zusammenhänge und Eigenschaften von Funktionen finden, die im Reellen verborgen bleiben, zum Beispiel die eulersche Identität. Hierüber erschließen sich vielfältige Anwendungsbereiche in der Physik (beispielsweise in der Quantenmechanik die Darstellung von Wellenfunktionen, sowie in der Elektrotechnik zweidimensionale Strom-Spannungs-Diagramme). Diese Identität ist auch die Basis für die komplexe Form der Fourier-Transformation. In vielen Fällen lässt sich diese einfach durch komplexe Analysis berechnen.
Für holomorphe Funktionen gilt, dass Real- und Imaginärteil harmonische Funktionen sind, also die Laplace-Gleichung erfüllen. Dies verknüpft die Funktionentheorie mit den partiellen Differentialgleichungen, beide Gebiete haben sich regelmäßig gegenseitig beeinflusst.
Das Wegintegral einer holomorphen Funktion ist vom Weg unabhängig. Dies war historisch das erste Beispiel einer Homotopieinvarianz. Aus diesem Aspekt der Funktionentheorie entstanden viele Ideen der algebraischen Topologie, beginnend mit Bernhard Riemann.
Außerdem kann man die Wegunabhängigkeit verwenden, um reelle Integrale zu berechnen, indem man die Integration in der komplexen Ebene durchführt (siehe Residuensatz).
In der Theorie der komplexen Banachalgebren spielen funktionentheoretische Mittel ein wichtige Rolle. Der holomorpher Funktionalkalkül erlaubt die Anwendung holomorpher Funtionen auf Elemente einer Banachalgebra. Eine weitere Anwendung funktionentheoretischer Methoden zeigt der Satz von Gelfand-Mazur.
Weitere wichtige Themen und Ergebnisse
Wichtige Ergebnisse sind der cauchysche Integralsatz, der Residuensatz und der riemannsche Abbildungssatz. Ein weiteres wichtiges Ergebnis ist der Fundamentalsatz der Algebra. Er besagt, dass sich ein Polynom im Bereich der komplexen Zahlen vollständig in Linearfaktoren zerlegen lässt. Für Polynome im Bereich der reellen Zahlen ist dies im Allgemeinen (mit reellen Linearfaktoren) nicht möglich.
Weitere wichtige Forschungsschwerpunkte sind die analytische Fortsetzbarkeit von holomorphen und meromorphen Funktionen auf die Grenzen ihres Definitionsbereiches und darüber hinaus.
Siehe auch
Grundlagen
Wichtige Sätze
- Cauchyscher Integralsatz
- Cauchysche Integralformel
- Satz von Liouville
- Residuensatz
- Riemannscher Abbildungssatz
- Riemannscher Hebbarkeitssatz
- Satz von Picard
- Satz von Morera
Ganze Funktionen
Meromorphe Funktionen
Literatur
- Lars Ahlfors: Komplex Analysis. McGraw-Hill Comp., 1953.
- Ludwig Bieberbach: Lehrbuch der Funktionentheorie. Bände 1. u.2., BG Teubner, 1923.
- Rolf Busam, Eberhard Freitag: Funktionentheorie 1. 4. Auflage. Springer, Berlin 2006, ISBN 3-540-31764-3.
- Durege: Elemente der Theorie der Funkt. einer komplexen Veränderlichen Grösse. 1.-5. Auflage. BG Teubner, 1882-1906.
- Wolfgang Fischer, Ingo Lieb: Funktionentheorie. 8. Auflage. Vieweg, Braunschweig 2003, ISBN 2-528-67247-1.
- J. A. Gmeiner, O. Stolz: Einleitung in die Funktionentheorie. Bände 1. u.2., BG Teubner, 1904.
- Klaus Jänich: Funktionentheorie. 6. Auflage. Springer, Berlin 2004, ISBN 3-540-20392-3.
- W. F. Osgood: Lehrbuch der Funktionentheorie. Bände 1.2.3., BG Teubner, 1923.
- Alfred Pringsheim: Vorlesungen über Funktionenlehre. BGTeubner, 1925. (Weierstrasscher Standpunkt)
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Berlin 2002, ISBN 3-540-59075-7.
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 2. 3. Auflage. Springer, Berlin 2007, ISBN 3-540-40432-5.
- Volker Scheidemann: Introduction to complex analysis in several variables. Birkhäuser, Basel 2005, ISBN 3-764-37490-X.
- Ian Stewart, David Tall: Complex Analysis. Cambridge University Press, 1997, ISBN 0-521-24513-3.
- Thomae: Elementare Theorie der analytischen Funktionen. Verlag Louis Nebert, 1898.
Wikimedia Foundation.