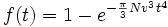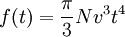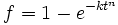Avrami-Theorie

Die Johnson-Mehl-Avrami-Kolmogorow-Gleichung (kurz: JMAK-Gleichung, auch Avrami-Gleichung) beschreibt den Ablauf einer Phasen- oder Gefügeumwandlung bei gleich bleibender Temperatur (Isotherme Zustandsänderung). Mithilfe der Gleichung erhält man eine ungefähre Kristallisationsrate. Die JMAK-Gleichung beschreibt den gesamten Vorgang der Umwandlung mit zwei Größen, der Nukleationsrate und der Geschwindigkeit des Wachstums bereits gebildeter Bereiche der neuen Phase.

Grundlagen

Wachstum einer Phase β in der Phase α: Keime entstehen an Nukleationszentren N. Das obere Bild zeigt einen früheren Zustand, das untere einen späteren.

Die Umwandlung einer Phase in eine andere, z. B. die Kristallisation eines amorphen Festkörpers, geschieht nicht überall zugleich, sondern beginnt an wenigen Punkten (Nukleation). Von diesen Punkten aus wächst die neue Phase (z. B. die Kristallite); im Laufe der Zeit werden die Bereiche dieser Phase immer größer. Außerdem findet Nukleation immer wieder an neuen Stellen statt, auch dadurch wird ein immer größerer Anteil in die neue Phase umgewandelt. Die Bereiche der neuen Phase wachsen zusammen, und es bleiben immer kleinere Reste der ursprünglichen Phase übrig, die schlussendlich ganz verschwinden. Die JMAK-Gleichung gibt an, wie groß der Anteil der neuen Phase am Gesamtsystem in Abhängigkeit von der Zeit ist.

Voraussetzung für das hier beschriebene Verhalten ist ein System, das zuerst aus einer Phase (hier α) besteht, obwohl eine andere Phase (β) thermodynamisch stabiler ist. Dies tritt zum Beispiel ein, wenn beim Abkühlen einer Legierung die Löslichkeit eines Elementes so weit sinkt, dass die Legierung übersättigt ist, also wenn mehr von diesem Element im Festkörper ist, als darin in Lösung bleiben kann.

Die JMAK-Gleichung ist eine wichtige Grundlage für die Erstellung von Zeit-Temperatur-Umwandlungs-(ZTU-)Schaubildern.

Anwendungen

Die Johnson-Mehl-Avrami-Kolmogorov-Gleichung beschreibt zahlreiche Prozesse in den Materialwissenschaften, insbesondere der Metallurgie, und in der physikalischen Chemie:

• Kristallisation in einem amorphen Festkörper (z. B. Polymer).
• Phasenumwandlungen mit der Temperatur, z. B. wenn oberhalb einer Grenztemperatur eine, unterhalb eine andere Kristallstruktur thermodynamisch stabil ist.
• In Legierungen beim Abkühlen: Bildung von Präzipitaten (Ausscheidungen) schlecht löslicher Elemente oder von Kristalliten mit intermetallischen Phasen, die ein oder mehrere schlecht lösliche Elemente enthalten (hier wird allerdings nur der Anfang des Prozesses beschreiben, weil es ja zu keiner vollständigen Umwandlung des gesamten Festkörpers kommt).
• Chemische Reaktionen mit einer Reaktionsfront, wenn die Reaktion nahe am thermodynamischen Gleichgewicht stattfindet.

In vielen Fällen beschreibt die JMAK-Gleichung vor allem den Anfang der Umwandlung gut, während gegen Ende der Umwandlung Abweichungen vom JMAK-Verhalten auftreten können. Bei der Bildung von Kristallen kann dies beispielsweise damit zusammenhängen, dass verschieden orientierte Kristalle zusammenstoßen und energetisch ungünstige Grenzflächen zwischen diesen Kristallen entstehen.

Mathematische Behandlung

Betrachtet wird die Ausscheidung einer Phase β aus der metastabilen Phase α. Unter den Annahmen einer konstanten Nukleationsrate, einer konstanten Wachstumsgeschwindigkeit der Keime, einer zufälligen Verteilung der Keime im Volumen, und sphärischen Keimen, ergibt sich der Anteil des umgewandelten Gefüges f(t) mit der Zeit t zu:

$f(t) = 1 - e^{- \frac{\pi}{3} N v^{3} t^{4}}$

Dabei repräsentiert N die konstante Nukleationsrate, mit der neue Keime gebildet werden, und v die Wachstumsgeschwindigkeit der Teilchen.

Diese Gleichung gilt für kurze und lange Umwandlungszeiten t, und kleine und große Umwandlungsanteile f. Für lange Zeiten, 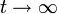$t \to \infty$, wo es zum Zusammenstoß der wachsenden Teilchen kommt, oder zur Überlappung ihrer Diffusionseinzugsgebiete, geht der Anteil f gegen eins, 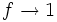$f \to 1$. Für kurze Zeiten, wo die Teilchen noch unabhängig von einander wachsen, und wo 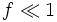$f \ll 1$ gilt, lässt sich die JMAK-Gleichung vereinfachen zu:

$f(t) = \frac{\pi}{3} N v^{3} t^{4}$

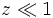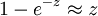Dabei wird von der Gesetzmäßigkeit Gebrauch gemacht, dass für $z \ll 1$ gilt: $1 - e^{-z} \approx z$. Die letzte Gleichung kann (vereinfacht) so erklärt werden: Die Anzahl der Keime wächst gemäß Nt, und der Radius jedes einzelnen Keims wächst linear, also sein Volumen mit (vt)³. Daher steigt am Anfang das Gesamtvolumen aller Keime mit t⁴. Erst wenn die Keime größer werden und zusammenwachsen, und zugleich das verbleibende noch nicht umgewandelte Gebiet, wo neue Keime entstehen können, immer kleiner wird, steigt das Volumen des umgewandelten Bereichs langsamer als mit t⁴.

Beide Gleichungen sind mit den anfänglichen Annahmen über Keimformen und deren Wachstum, Spezialfälle einer allgemeineren Gesetzmäßigkeit, die auch für eine Vielzahl anderer Modelle gültig ist:

$f = 1 - e^{- k t^{n}}$

Der sog. Avrami-Exponent n ist dabei ein numerischer Exponent von 1 bis 4. Beispielsweise erhält man in zwei Dimensionen (Kristallisation in einer sehr dünnen Schicht) einen Exponenten von n = 3. Die Konstante k hängt von der Nukleationsrate und Wachstumsgeschwindigkeit ab. Da N und v selber von der Temperatur abhängig sind, ist somit k auch von der Temperatur abhängig.

Literatur

• A. N. Kolmogorov, Statistical theory of crystallization of metals. (in russisch), Izvestia Akademia Nauk SSSR Ser. Mathematica (Izv. Akad. Nauk SSSR, Ser. Mat; Bull. Acad. Sci. USSR. Ser. Math)., 1, 1937, S. 355–359
• W. A. Johnson, R. F. Mehl, Reaction Kinetics in processes of nucleation and growth, Transactions of American Institute of Mining and Metallurgical Engineers (Trans. Am. Inst. Min. Metall. Eng.), 135, 1939, S. 416–458
• M. Avrami, Kinetics of phase change. III: Granulation, Phase Change an Microstructures., Journal of Chemical Physics (J. Chem. Phys.), 9, 1941, S. 177–184
• M. Fanfoni, M. Tomellini, The Johnson-Mehl-Avrami-Kolmogorov model: A brief review, Il Nuovo Cimento D, 20, 1998, S. 1171–1182
• M. C. Weinberg, D. P. Birnie III, V. A. Shneidman, Crystallization kinetics and the JMAK equation, Journal of Non-Crystalline Solids, Volume 219, 1 Oktober 1997, S. 89–99, Abstract

Siehe auch

• Nukleation
• Moussierpunkt
• Phasenübergang
• Unterkühlung (Thermodynamik), Siedeverzug
• Kristallisationskeim, Kondensationskeim