Ruhelage

Als kritischer Punkt (auch: Fixpunkt, Gleichgewichtspunkt oder Ruhelage) wird in der Theorie dynamischer Systeme ein Punkt im Phasenraum bezeichnet, an dem sich die zeitliche Entwicklung des Systems nicht ändert. Je nachdem, ob Trajektorien, die nahe einem solchen Punkt liegen, angezogen oder abgestoßen werden, wird der Punkt als stabil oder instabil bezeichnet. Eine ruhende Kugel in einer Mulde ist ein Beispiel für einen stabilen Fixpunkt, ein auf dem Kopf stehendes, ausbalanciertes Pendel ist in einer instabilen Ruhelage. Durch Berechnung kritischer Punkte und deren Stabilität (lineare Stabilitätsanalyse) kann die zeitliche Entwicklung eines dynamischen Systems charakterisiert werden, ohne zum Beispiel die zugehörigen Differentialgleichungen lösen zu müssen.

Ist das System durch eine Differentialgleichung der Form 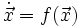$\dot{\vec{x}} = f(\vec{x})$ gegeben, ist eine Ruhelage bzw. Fixpunkt 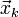$\vec{x}_k$ durch die Bedingung 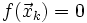$f(\vec{x}_k) = 0$ gegeben. Je nach Anzahl der Lösungen für diese Gleichung kann das System beliebig viele kritische Punkte besitzen. Liegt dem System eine iterierte Abbildung 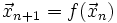$\vec{x}_{n+1} = f(\vec{x}_n)$ zugrunde, lautet die Fixpunktbedingung 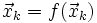$\vec{x}_k = f(\vec{x}_k)$. In beiden Fällen ist der Zustand 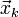$\vec{x}_k$ zu allen Zeiten der gleiche, man sagt auch "invariant gegenüber der Dynamik f".

Siehe auch: Gleichgewicht (Physik), Dynamisches System, Stabilitätstheorie