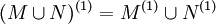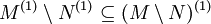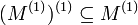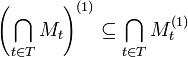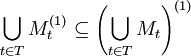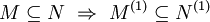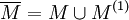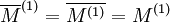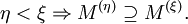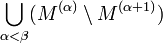Satz von Cantor-Bendixson

Unter der Ableitung einer Menge versteht man in der Mathematik die Menge der Häufungspunkte einer Menge. Vorausgesetzt wird dabei, dass auf der Menge ein Abstandsbegriff oder allgemeiner eine Topologie definiert ist.^[1] Präziser spricht man auch von der ersten Ableitung. Ein gleichbedeutender Begriff ist die Derivierte^[2] der Menge. Heißt die Menge M, so sind Zeichen für ihre Ableitung M^{${\ }^\prime$}, M^d oder, für die erste Ableitung, M⁽¹⁾.

Höhere Mengenableitungen

Höhere Mengenableitungen werden induktiv definiert: Die n-te Ableitung M⁽ⁿ⁾ ist die Ableitung der n − 1-ten Ableitung M^{(n − 1)}. Die abgeschlossene Hülle von M wird auch als die nullte Ableitung von M bezeichnet. Allgemeiner wird für jede isolierte Ordinalzahl ξ die ξ-te Ableitung M^(ξ) durch M^(ξ) = (M^{(ξ − 1)})⁽¹⁾ und für jede Limeszahl ξ durch 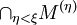$\cap_{\eta<\xi}M^{(\eta)}$ definiert.^[3]

Eigenschaften

Die Ableitung einer Menge kann leer sein. In einem T₁-Raum gelten folgende Regeln:^[3]

• $(M\cup N)^{(1)}=M^{(1)}\cup N^{(1)}$
• $M^{(1)}\setminus N^{(1)}\subseteq (M\setminus N)^{(1)}$
• $( M^{(1)} )^{(1)} \subseteq M^{(1)}$
• $\left(\bigcap_{t\in T} M_t \right)^{(1)} \subseteq \bigcap_{t\in T} M_t^{(1)}$
• $\bigcup_{t\in T} M_t^{(1)} \subseteq \left(\bigcup_{t\in T} M_t \right)^{(1)}$
• $M\subseteq N\ \Rightarrow\ M^{(1)}\subseteq N^{(1)}$
• $\overline{M}=M\cup M^{(1)}$
• $\overline{M}^{(1)}=\overline{M^{(1)}}=M^{(1)}$
• $\eta<\xi \Rightarrow M^{(\eta)}\supseteq M^{(\xi)}.$

Eine Menge M ist genau dann perfekt, wenn M⁽¹⁾ = M. Der insichdichte Kern einer Menge ist der Durchschnitt seiner Ableitungen.^[4]

Räume mit abzählbarer Basis

Sei 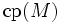$\operatorname{cp}(M)$ die Menge der Kondensationspunkte von M. In einem topologischen Raum mit abzählbarer Basis ist 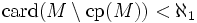$\operatorname{card}(M\setminus \operatorname{cp}(M))<\aleph_1$ (Erster Satz von Lindelöf)^[5], und jede abgeschlossene Menge lässt sich als Vereinigung von einer perfekten und einer höchstens abzählbaren Menge darstellen (Satz von Cantor-Bendixson, I). In polnischen Räumen ist diese Darstellung eindeutig^[6], und jede abgeschlossene Menge ist entweder höchstens abzählbar oder hat die Mächtigkeit des Kontinuums.

In Räumen mit abzählbarer Basis endet für jede Teilmenge die Folge ihrer Ableitungen immer mit einer perfekten Menge, d.h. für jede Menge M existiert eine Ordinalzahl ξ < Ω, so dass M^(ξ) = M^{(ξ + 1)} (Satz von Cantor-Bendixson, II)^[5]. Die kleinste derartige Ordinalzahl heißt Cantor-Bendixsonscher Grad der Menge.

Der zweite Satz von Cantor-Bendixson ist eine Verallgemeinerung des ersten. Man betrachte die auf M durch X induzierte Topologie. Wenn β der Cantor-Benidixsonsche Grad der Menge M in diesem Raum ist, dann ist

$M = \bigcup_{\alpha &amp;lt; \beta}(M^{(\alpha)} \setminus M^{(\alpha+1)}) \cup M^{(\beta)}$.

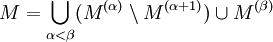Die Mengen M^(α) \ M^{(α + 1)} bestehen nur aus isolierten Punkten und sind höchstens abzählbar. Die Menge

$\bigcup_{\alpha &amp;lt; \beta}(M^{(\alpha)} \setminus M^{(\alpha+1)})$

ist als Vereinigung von höchstens abzählbar vielen höchstens abzählbaren Mengen selbst höchstens abzählbar. Die Menge M^(β) ist wegen M^(β) = M^{(β + 1)} perfekt.

Einzelnachweise

1. ↑ Über die Geschichte der Einführung des Begriffes Mengenableitung durch G. Cantor können sie in Ordinalzahl: Geschichte der Entdeckung erfahren.
2. ↑ Rinow W., Lehrbuch der Topologie, 1975, VEB Deutscher Verlag der Wissenschaften, ISBN 978-3326004334
3. ↑ ^{a b} Kuratowski C., Topology, Vol. I, Academic Press, New York-London, 1966, ISBN 0-12-429201-1, § 9., § 24.IV
4. ↑ Naas J., Schmid H.L., Mathematisches Wörterbuch, B.G. Teubner Stuttgart, 1979, ISBN 3-519-02400-4
5. ↑ ^{a b} Alexandroff P.S., Lehrbuch der Mengenlehre, Verlag Harri Deutsch, Frankfurt am Main, 1994, ISBN 3-8171-1365-X
6. ↑ Deiser O., Reelle Zahlen. Das klassische Kontinuum und die natürlichen Folgen, Springer, 2007, ISBN 978-3540453871