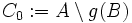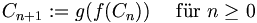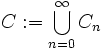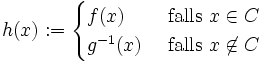- Satz von Cantor-Bernstein
-
In der Mengenlehre ist das Cantor-Bernstein-Schröder-Theorem (in der Literatur uneinheitlich auch als Satz von Cantor-Bernstein, als Äquivalenzsatz von Cantor-Bernstein oder auch als Satz von Schröder-Bernstein bezeichnet) eine Aussage über die Mächtigkeiten zweier Mengen. Es ist benannt nach den Mathematikern Georg Cantor, Felix Bernstein und Ernst Schröder und ist ein wichtiges Hilfsmittel beim Nachweis der Gleichmächtigkeit zweier Mengen.
Inhaltsverzeichnis
Satz
Das Cantor-Bernstein-Schröder-Theorem lautet:
- Sei eine Menge A gleichmächtig zu einer Teilmenge einer Menge B, und sei B gleichmächtig zu einer Teilmenge von A. Dann sind A und B gleichmächtig.
Dabei heißen zwei Mengen gleichmächtig, wenn es eine bijektive Abbildung zwischen ihnen gibt. Ausgedrückt durch die Mächtigkeiten von A und B lautet das Theorem:
- Aus
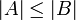 und
und 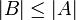 folgt | A | = | B | .
folgt | A | = | B | .
Dabei gilt | A | = | B | genau dann, wenn A und B gleichmächtig sind, und
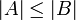 gilt genau dann, wenn A gleichmächtig zu einer Teilmenge von B ist, d.h. wenn es eine injektive Abbildung von A in B gibt. Ausgedrückt durch die Eigenschaften von Funktionen lautet das Theorem:
gilt genau dann, wenn A gleichmächtig zu einer Teilmenge von B ist, d.h. wenn es eine injektive Abbildung von A in B gibt. Ausgedrückt durch die Eigenschaften von Funktionen lautet das Theorem:Der Äquivalenzsatz wurde 1883 von Georg Cantor formuliert, aber erst 1897 von Felix Bernstein in einem von Cantor geleiteten Seminar und etwa gleichzeitig unabhängig von Ernst Schröder bewiesen.[1][2]
Beweisidee
Wir geben hier eine Beweisidee (zuerst gegeben von Eilenberg?).
Wir definieren die Mengen
Für jedes x aus A setzen wir dann
Da im Falle, dass x nicht in C ist, x in g(B) liegen muss, gibt es ein eindeutig bestimmtes Element g-1(x) und h ist eine wohldefinierte Abbildung von A nach B.
Man kann nun zeigen, dass diese Funktion h: A -> B die gewünschte Bijektion ist.
Beachte, dass diese Definition von h nicht konstruktiv ist, d.h. es gibt kein Verfahren, um für beliebige Mengen A, B und Injektionen f, g in endlich vielen Schritten zu entscheiden, ob ein x aus A in C liegt oder nicht. Für spezielle Mengen und Abbildungen kann das natürlich möglich sein.
Veranschaulichung
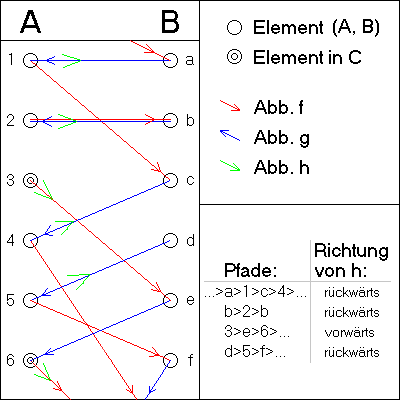
Veranschaulichen kann man sich die Definition von h anhand der folgenden Darstellung.
Dargestellt sind Teile der (disjunkten) Mengen A und B sowie die Abbildungen f und g. Betrachtet man A vereinigt B als Graphen, dann zerfällt der Graph in verschiedene Zusammenhangskomponenten. Diese lassen sich in vier Typen einteilen: beidseitig unendliche Pfade; endliche Zyklen; unendliche Pfade, die in A beginnen; unendliche Pfade, die in B beginnen (von jedem Typ ist hier einer vertreten, da der Pfad durch das Element a beidseitig unendlich sein soll). Es ist aber allgemein nicht in endlich vielen Schritten entscheidbar, welchen Typ der durch ein vorgegebenen Element gehende Pfad hat.
Die oben definierte Menge C enthält nun genau die Elemente von A, die Teil eines in A beginnenden Pfades sind. Die Abbildung h wird so definiert, dass sie innerhalb einer jeden Zusammenhangskomponente eine Bijektion der A-Elemente auf "im Pfad benachbarte" B-Elemente herstellt (dabei hat man bei den beidseitig unendlichen Pfaden und den endlichen Zyklen eine Richtungswahl und wir legen uns auf "rückwärts" fest).
Ein kurzer und leicht verständlicher Beweis findet sich auch in dem Göschenbändchen "Mengenlehre" von Erich Kamke.
Siehe auch
- Vergleichbarkeitssatz
- Artikel zum Satz auf matheplanet.com: http://matheplanet.com/matheplanet/nuke/html/article.php?sid=873
Einzelnachweise
- ↑ Oliver Deiser: Einführung in die Mengenlehre. Berlin 2004. ISBN 3-540-20401-6
- ↑ Patrick Suppes: Axiomatic Set Theory. Dover Publications 1972. ISBN 0-486-61630-4
Wikimedia Foundation.

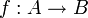
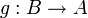 .
. 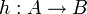 .
.