Satz von Cramer

Der Satz von Cramér (nach dem schwedischen Mathematiker Harald Cramér) ist die Umkehrung der bekannten Aussage, dass die Summe unabhängiger normalverteilter Zufallsvariablen wieder normalverteilt ist.

Satz von Cramér

Ist eine normalverteilte Zufallsvariable X die Summe von zwei unabhängigen Zufallsvariablen X₁ und X₂, dann sind die Summanden X₁ und X₂ ebenfalls normalverteilt.

Eine normalverteilte Zufallsvariable lässt sich also nur in normalverteilte unabhängige Summanden zerlegen.

Man beachte dazu auch die "Gegenaussage" des zentralen Grenzwertsatzes, nach dem die Summe einer großen Anzahl von unabhängigen nicht notwendig normalverteilten Summanden annähernd normalverteilt ist.

Der Satz von Cramér hat eine gewisse Stabilität gegenüber kleinen Abweichungen: Ist die Summe X₁ + X₂ (in einem bestimmten Sinne) annähernd normalverteilt, dann sind es auch die Summanden.

Der Satz wurde ursprünglich von Paul Lévy ^[1] formuliert, aber erst kurz danach von Harald Cramér ^[2] bewiesen.Er wird deshalb manchmal auch als Satz von Lévy-Cramér bezeichnet, was aber zu Verwechslungen mit anderen Sätzen dieses Namens führen kann.

Beweisskizze

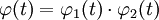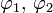Der Beweis lässt sich sehr elegant durch Anwendung analytischer Eigenschaften charakteristischer Funktionen führen: Aus der Zerlegung X = X₁ + X₂ folgt für die zugehörigen charakteristischen Funktionen $\varphi (t) = \varphi_1 (t) \cdot \varphi_2 (t)$. Die Funktion $\varphi$ ist eine ganze Funktion der Wachstumsordnung 2 ohne Nullstellen, deshalb sind die Faktoren $\varphi_1, \, \varphi_2$ ebenfalls ganze Funktionen mit einer Wachstumsordnung höchstens 2. Daraus folgt (am Beispiel des ersten Faktors) die Darstellung 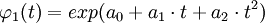$\varphi_1 (t) = exp (a_0 + a_1 \cdot t + a_2 \cdot t^2 )$. 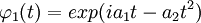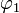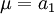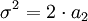Aus elementaren Eigenschaften charakteristischer Funktionen folgt daraus schließlich die Darstellung $\varphi_1 (t) = exp (ia_1t - a_2t^2 )$, so dass $\varphi_1$ die charakteristische Funktion einer normalverteilten Zufallsvariablen mit Parametern $\mu = a_1\,$ und $\sigma^2 = 2\cdot a_2$ ist.

Diese Beweisskizze demonstriert sehr gut das Zusammenwirken unterschiedlicher mathematischer Disziplinen, hier der Stochastik und der klassischen Funktionentheorie.

Literatur

• Eugen Lukacs: Characteristic functions. Griffin, London 1960 (2., erweiterte Auflage 1970), ISBN 0-852-64170-2

Einzelnachweise

1. ↑ Paul Lévy, "Propriétés asymptotiques des sommes de variables aléatoires indépendantes ou enchaînées", J. Math. Pures Appl., 14 (1935), S. 347–402
2. ↑ Harald Cramér, "Ueber eine Eigenschaft der normalen Verteilungsfunktion", Math. Z., 41 (1936), S. 405–414