Satz von Eberlein–Smulian

Der Satz von Eberlein–Šmulian (nach William Frederick Eberlein und Witold Lwowitsch Šmulian) ist ein mathematischer Satz aus der Funktionalanalysis, der eine Aussage über Kompaktheitseigenschaften bezüglich der schwachen Topologie eines Banachraums macht.

In der Topologie wird die Folgenkompaktheit als Variante der Kompaktheit untersucht. Keiner dieser beiden Begriffe folgt aus dem jeweils anderen. Sei zum Beispiel X die Einheitskugel im Dualraum des Folgenraums 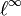$\ell^\infty$. Mit der schwach-*-Topologie ist X nach dem Satz von Banach-Alaoglu kompakt. X ist nicht folgenkompakt, denn ist 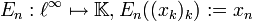$E_n:\ell^\infty \mapsto {\mathbb K}, E_n((x_k)_k) := x_n$, so ist (E_n)_n eine Folge in X, die keine konvergente Teilfolge hat. Umgekehrt gibt es folgenkompakte Räume, die nicht kompakt sind.

Es ist ein bekannter Satz, dass in metrischen Räumen die Begriffe Kompaktheit und Folgenkompaktheit zusammenfallen. Da die schwache Topologie auf einem Banachraum nicht metrisierbar ist, außer im endlich-dimensionalen Fall, ist der folgende Satz von Eberlein–Šmulian bemerkenswert.

Der Satz von Eberlein–Šmulian

Sei X eine nicht-leere Teilmenge eines Banachraums. Dann sind folgende Aussagen äquivalent:

• Der schwache Abschluss von X ist schwach-kompakt (d.h. kompakt bzgl. der schwachen Topologie).
• Der schwache Abschluss von X ist schwach-folgenkompakt (d.h. folgenkompakt bzgl. der schwachen Topologie).

Bemerkungen

1. Für schwach-abgeschlossene Teilmengen eines Banachraums fallen daher die Begriffe kompakt und folgenkompakt zusammen.
2. Ein vergleichbarer Satz für die schwach-*-Topologie gilt nicht, wie das eingangs gegebene Beispiel der Einheitkugel in 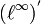$(\ell^\infty)^'$ zeigt.
3. Šmulian hat 1940 gezeigt, dass schwach-kompakte Mengen in Banachräumen schwach-folgenkompakt sind. Die Umkehrung wurde erst 1947 von Eberlein gezeigt. Diese Umkehrung wurde 1952 von Alexander Grothendieck auf lokalkonvexe Räume, die bezüglich ihrer Mackey-Topologie quasivollständig sind, verallgemeinert.
4. Ist X eine schwach-kompakte Teilmenge in einem Banachraum, so weist sie folgende Besonderheit auf: Eine Teilmenge 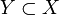$Y\subset X$ ist genau dann schwach-abgeschlossen, wenn sie schwach-folgenabgeschlossen ist, d.h. wenn sie mit jeder konvergenten Folge auch den Grenzwert enthält. Es ist klar, dass abgeschlossene Mengen folgenabgeschlossen sind. Ist umgekehrt 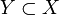$Y\subset X$ folgenabgeschlossen, so ist Y als Teilmenge des nach obigem Satz folgenkompakten Raumes X folgenkompakt und daher, wieder nach dem Satz von Eberlein-Šmulian, schwach-kompakt und damit schwach abgeschlossen.

Quellen

• Joseph Diestel: Sequences and Series in Banach Spaces. 1984, ISBN 0-387-90859-5.