- Satz von Poincaré-Birkhoff-Witt
-
Die universelle einhüllende Algebra (auch universelle Einhüllende) ist ein Begriff aus dem mathematischen Teilgebiet der Theorie der Liealgebren. Sie ist eine assoziative Algebra, die zeigt, dass man die Lieklammer stets als Kommutator auffassen kann, auch bei Liealgebren, die nicht von einer assoziativen Algebra herkommen.
Inhaltsverzeichnis
Definition
Es sei
 eine Liealgebra (über einem Körper). Eine universelle einhüllende Algebra
eine Liealgebra (über einem Körper). Eine universelle einhüllende Algebra 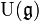 von
von  besteht aus einer unitären assoziativen Algebra und einem Liealgebrenhomomorphismus
besteht aus einer unitären assoziativen Algebra und einem Liealgebrenhomomorphismus 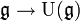 (dabei sei die Liealgebrastruktur auf assoziativen Algebren durch den Kommutator gegeben), so dass gilt:
(dabei sei die Liealgebrastruktur auf assoziativen Algebren durch den Kommutator gegeben), so dass gilt:- Ist A eine unitäre assoziative Algebra, so stehen die Liealgebrahomomorphismen
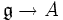 in Bijektion mit den unitären Algebrenhomomorphismen
in Bijektion mit den unitären Algebrenhomomorphismen 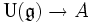 . Diese Bijektion wird durch den Homomorphismus
. Diese Bijektion wird durch den Homomorphismus 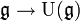 vermittelt.
vermittelt.
Eigenschaften
- Die wichtigste Aussage über universelle einhüllende Algebren ist der Satz von Poincaré-Birkhoff-Witt (nach Henri Poincaré, Garrett Birkhoff und Ernst Witt; auch als PBW abgekürzt): Ist
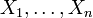 eine Basis von
eine Basis von  und
und 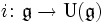 die kanonische Abbildung, so bilden die Monome
die kanonische Abbildung, so bilden die Monome
-
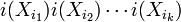 mit
mit 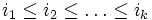
- eine Basis von
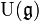 .
.
- Insbesondere ist i injektiv, und jede Liealgebra ist Unteralgebra einer assoziativen Algebra.
- Moduln unter einer Liealgebra sind dasselbe wie Moduln unter ihrer universellen einhüllenden Algebra.
Konstruktion
Man kann die universelle Einhüllende explizit angeben als Quotienten der Tensoralgebra
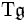 nach dem zweiseitigen Ideal, das von Elementen der Form
nach dem zweiseitigen Ideal, das von Elementen der Formfür
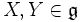 erzeugt wird. Man beachte: Im Unterschied zu den entsprechenden Konstruktionen der äußeren Algebra oder symmetrischen Algebra ist dieses Ideal nicht homogen,
erzeugt wird. Man beachte: Im Unterschied zu den entsprechenden Konstruktionen der äußeren Algebra oder symmetrischen Algebra ist dieses Ideal nicht homogen, 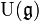 trägt also keine induzierte Graduierung.
trägt also keine induzierte Graduierung.Beispiele
- Ist
 abelsch, so ist die universelle einhüllende Algebra isomorph zur symmetrischen Algebra über
abelsch, so ist die universelle einhüllende Algebra isomorph zur symmetrischen Algebra über  .
.
- Ist A eine unitäre assoziative Algebra, so stehen die Liealgebrahomomorphismen
Wikimedia Foundation.

![X\otimes Y-Y\otimes X-[X,Y]](/pictures/dewiki/101/efa058d8548e9c2c9d27cf84332bdfff.png)