- Satz von Pontrjagin
-
Die Pontrjagin-Dualität (nach Lew Semjonowitsch Pontrjagin) ist ein mathematischer Begriff aus der harmonischen Analyse. Einer lokalkompakten abelschen Gruppe wird eine weitere lokalkompakte abelsche Gruppe als Dualgrupe zugeordnet, derart dass die Dualgruppe zur Dualgruppe wieder die Ausgangsgruppe ist. Diese Konstruktion spielt eine wichtige Rolle in der abstrakten Fourier-Transformation und der Struktur-Theorie der lokalkompakten abelschen Gruppen.
Inhaltsverzeichnis
Pontrjagin-Dualität
Die Kreislinie
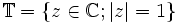 ist mit der Multiplikation als Gruppenverknüpfung eine kompakte Gruppe.
ist mit der Multiplikation als Gruppenverknüpfung eine kompakte Gruppe.Ist G eine lokalkompakte abelsche Gruppe, so heißt ein stetiger Gruppenhomomorphismus
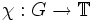 ein Charakter von G. Die Dualgruppe
ein Charakter von G. Die Dualgruppe 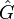 von G ist die Menge aller Charaktere von G. Mit der Multiplikation
von G ist die Menge aller Charaktere von G. Mit der Multiplikation 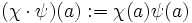 wird
wird 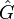 zu einer abelschen Gruppe, und die Topologie der kompakten Konvergenz macht
zu einer abelschen Gruppe, und die Topologie der kompakten Konvergenz macht 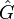 zu einer lokalkompakten Gruppe, d.h. zu einer topologischen Gruppe, deren Topologie lokalkompakt ist.
zu einer lokalkompakten Gruppe, d.h. zu einer topologischen Gruppe, deren Topologie lokalkompakt ist.Ist
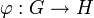 ein stetiger Homomorphismus, so ist
ein stetiger Homomorphismus, so ist 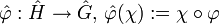 ebenfalls ein stetiger Homomorphismus, der zu
ebenfalls ein stetiger Homomorphismus, der zu  duale Homomorphismus.
duale Homomorphismus.Beispiele
- Die Charaktere der Restklassengruppe
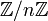 haben die Form
haben die Form ![\chi_m: {\mathbb Z}/n{\mathbb Z}\rightarrow {\mathbb T},\, \chi_m([k])=e^{2\pi i k m/n}](/pictures/dewiki/100/d62ec9e55570cb3cf79b23a4457228e3.png) , wobei
, wobei 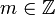 . Leicht sieht man
. Leicht sieht man 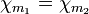 , falls
, falls 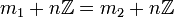 , und damit
, und damit 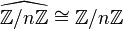 .
. - Jeder Charakter von
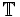 hat die Form χn(z) = zn für ein
hat die Form χn(z) = zn für ein 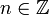 . Identifiziert man χn mit n, so sieht man leicht
. Identifiziert man χn mit n, so sieht man leicht 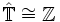 .
. - Die Gruppe
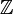 hat die Charaktere
hat die Charaktere 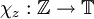 , χz(n) = zn, wobei
, χz(n) = zn, wobei 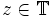 . Die Zuordnung
. Die Zuordnung 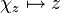 liefert
liefert 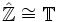 .
.  mit der Addition als Verknüpfung und der euklidischen Topologie ist eine lokalkompakte abelsche Gruppe. Jeder Charakter
mit der Addition als Verknüpfung und der euklidischen Topologie ist eine lokalkompakte abelsche Gruppe. Jeder Charakter 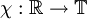 hat die Gestalt χz(x) = eixz für ein
hat die Gestalt χz(x) = eixz für ein 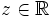 . Identifiziert man χz mit z, so hat man also
. Identifiziert man χz mit z, so hat man also 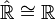 zunächst als Mengen. Dabei gilt
zunächst als Mengen. Dabei gilt 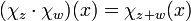 für alle
für alle 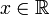 und die Abbildung
und die Abbildung 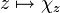 ist ein Homöomorphismus, also hat man
ist ein Homöomorphismus, also hat man 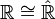 auch als lokalkompakte abelsche Gruppen.
auch als lokalkompakte abelsche Gruppen.
Produkte von Gruppen
Sind G und H lokalkompakte abelsche Gruppen, so auch deren kartesisches Produkt
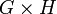 . Dann definiert
. Dann definiert 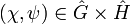 einen Charakter auf
einen Charakter auf 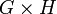 , wenn man
, wenn man 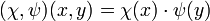 setzt. Auf diese Weise erhält man einen Gruppenhomöomorphismus
setzt. Auf diese Weise erhält man einen Gruppenhomöomorphismus 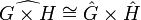 .
.Damit hat man viele weitere Beispiele:
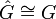 für jede endliche abelsche Gruppe G, denn eine solche ist endliches Produkt von Gruppen der Form
für jede endliche abelsche Gruppe G, denn eine solche ist endliches Produkt von Gruppen der Form 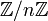 (siehe dazu: Endlich erzeugte abelsche Gruppe).
(siehe dazu: Endlich erzeugte abelsche Gruppe).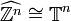 ,
, 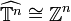 ,
, 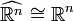
Dualitätssatz von Pontrjagin
Man hat eine natürliche Abbildung
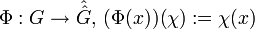 . Der Satz von Pontrjagin besagt, dass diese Abbildung stets ein topologischer Gruppenisomorphismus ist. Das rechtfertigt die Bezeichnung Dualgruppe von G, denn nach obigem Satz kann man G aus
. Der Satz von Pontrjagin besagt, dass diese Abbildung stets ein topologischer Gruppenisomorphismus ist. Das rechtfertigt die Bezeichnung Dualgruppe von G, denn nach obigem Satz kann man G aus 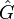 durch erneute Dualgruppenbildung zurückgewinnen.
durch erneute Dualgruppenbildung zurückgewinnen.Beziehungen zwischen Gruppe und Dualgruppe
Auf Grund der Pontrjagin-Dualität erwartet man eine Reihe von Beziehungen zwischen einer lokalkompakten abelschen Gruppe G und ihrer Dualgruppe
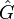 . Dabei findet man Beziehungen zwischen algebraischen und topologischen Eigenschaften. Exemplarisch gilt:
. Dabei findet man Beziehungen zwischen algebraischen und topologischen Eigenschaften. Exemplarisch gilt:Für eine kompakte Gruppe sind folgende Aussagen äquivalent:
- G ist zusammenhängend.
- G ist teilbar.
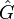 ist torsionsfrei.
ist torsionsfrei.
Eine weitere Zusammenhangseigenschaft führt zu folgender Äquivalenz:
- Eine kompakte Gruppe G ist genau dann total unzusammenhängend, wenn
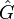 eine dividierbare Gruppe ist.
eine dividierbare Gruppe ist.
Ein stetiger Homomorphismus
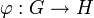 heißt strikt, wenn
heißt strikt, wenn  als Abbildung
als Abbildung 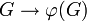 offen ist, d.h. das Bild jeder offenen Menge ist relativ offen im Bild von
offen ist, d.h. das Bild jeder offenen Menge ist relativ offen im Bild von  . Eine Folge
. Eine Folge 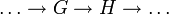 von Homomorphismen heißt strikt, wenn jeder Homomorphismus strikt ist. Bezeichnet man schließlich die einelementige Gruppe mit 1 und beachtet
von Homomorphismen heißt strikt, wenn jeder Homomorphismus strikt ist. Bezeichnet man schließlich die einelementige Gruppe mit 1 und beachtet 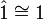 , so gilt folgender Satz:
, so gilt folgender Satz:- Sei
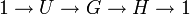 eine Folge stetiger Homomorphismen zwischen lokalkompakten abelschen Gruppen. Dann sind folgende Aussage äquivalent:
eine Folge stetiger Homomorphismen zwischen lokalkompakten abelschen Gruppen. Dann sind folgende Aussage äquivalent:
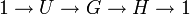 ist eine strikte und exakte Folge.
ist eine strikte und exakte Folge.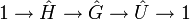 ist eine strikte und exakte Folge.
ist eine strikte und exakte Folge.
Daraus zieht man weitere Folgerungen:
- Ein stetiger Homomorphismus
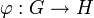 ist genau dann strikt, wenn
ist genau dann strikt, wenn 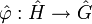 strikt ist.
strikt ist. - Ist
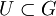 eine abgeschlossene Untergruppe, so ist
eine abgeschlossene Untergruppe, so ist 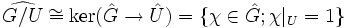 . Dabei ist
. Dabei ist 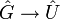 die zur Inklusion
die zur Inklusion 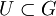 duale Abbildung.
duale Abbildung.
Kompakt erzeugte Gruppen
Die Pontrjagin-Dualität ist ein wichtiges Hilfsmittel in der Struktur-Theorie für lokalkompakte abelsche Gruppen. Eine lokalkompakte Gruppe heißt kompakt erzeugt, wenn es eine kompakte Teilmenge von G gibt, die G als Gruppe erzeugt. Eine diskrete Gruppe ist genau dann kompakt erzeugt, wenn sie endlich erzeugt ist.
Für eine lokalkompakte abelsche Gruppe sind äquivalent:
- G ist kompakt erzeugt.
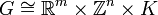 , wobei
, wobei 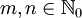 und K eine kompakte Gruppe ist.
und K eine kompakte Gruppe ist.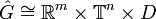 , wobei
, wobei 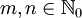 und D eine diskrete Gruppe ist.
und D eine diskrete Gruppe ist.
Zusatz: Dabei sind die Zahlen m und n eindeutig durch G bestimmt und K ist die größte kompakte Untergruppe von G.
Gelfand-Transformation
Wie im Artikel Harmonische Analyse erläutert, tritt die Dualgruppe einer lokalkompakten abelschen Gruppe G in der Gelfand-Transformation der Faltungsalgebra über G auf.
Pontrjagin-Dualität als Funktor
Die Pontrjagin-Dualität, d.h. die oben beschriebenen Zuordnungen
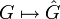 und
und  von lokalkompakten abelschen Gruppen und stetigen Homomorphismen, ist offenbar ein kontravarianter Funktor. Die zweifache Hintereinanderausführung dieses Funktors führt zum identischen Funktor (genauer: zu einer natürlichen Transformation zum identischen Funktor).
von lokalkompakten abelschen Gruppen und stetigen Homomorphismen, ist offenbar ein kontravarianter Funktor. Die zweifache Hintereinanderausführung dieses Funktors führt zum identischen Funktor (genauer: zu einer natürlichen Transformation zum identischen Funktor).Literatur
- Lynn H. Loomis, An Introduction to Abstract Harmonic Analysis, D. van Nostrand Co, 1953
- Walter Rudin, Fourier Analysis on Groups, 1962
- E. Hewitt, K. Ross, Abstract Harmonic Analysis I, II, Springer (1963), (1970).
- Die Charaktere der Restklassengruppe
Wikimedia Foundation.