Satz von der dominierten Konvergenz
- Satz von der dominierten Konvergenz
-
Der Satz von der majorisierten Konvergenz (auch Satz von der majorisierenden Konvergenz, Satz von der dominierten Konvergenz oder Satz von Lebesgue) ist eine zentrale Grenzwertaussage in der Maß- und Integrationstheorie und geht auf den französischen Mathematiker Henri Léon Lebesgue zurück.
Der Satz liefert ein Entscheidungskriterium für die Vertauschbarkeit von Integral- und Grenzwertbildung.
Der Satz formal in seiner allgemeinsten Form
Sei 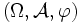 ein Maßraum und sei
ein Maßraum und sei  eine Folge von
eine Folge von  -messbaren Funktionen
-messbaren Funktionen 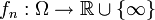 .
.
Die Folge  konvergiere
konvergiere  -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f. Ferner werde die Folge
-messbare Funktion f. Ferner werde die Folge  von einer
von einer  -integrierbaren Funktion
-integrierbaren Funktion 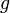 auf
auf 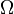 majorisiert, sprich für alle
majorisiert, sprich für alle  gelte
gelte 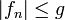
 -fast überall.
-fast überall.
Dann sind f und alle 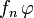 -integrierbar und es gilt:
-integrierbar und es gilt:
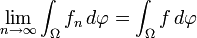 sowie
sowie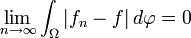
Bemerkung zur Voraussetzung
Auf die Voraussetzung der Majorisierbarkeit 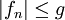 kann nicht verzichtet werden. Als Beispiel dient die Folge
kann nicht verzichtet werden. Als Beispiel dient die Folge 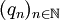 , definiert durch
, definiert durch ![q_n : [0,1] \rightarrow\mathbb{R}, q_n := n \chi_{[0,{1\over n}]}](/pictures/dewiki/97/a5c7bd967c41f8f56061fc6383142373.png) , worin
, worin ![\chi_{[0,{1\over n}]}](/pictures/dewiki/50/21c2f47dc5d6425b6633c0bd46a2bed5.png) die Indikatorfunktion auf
die Indikatorfunktion auf ![[0,{1 \over n}]](/pictures/dewiki/102/f709a04a682386d1aa36cf01125f791d.png) bezeichne.
bezeichne.
Es gilt 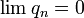 fast überall, aber dennoch ist
fast überall, aber dennoch ist ![\lim \int_{[0,1]} q_n = \lim 1 = 1 \ne 0 = \int_{[0,1]} 0 = \int_{[0,1]} \lim q_n](/pictures/dewiki/99/ccf495a5236cf75e90fc7aa230e5048a.png) .
.
Majorisierte Konvergenz in Lp-Räumen (Folgerung)
Sei 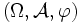 ein Maßraum,
ein Maßraum, 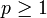 eine reelle Zahl und sei
eine reelle Zahl und sei  eine Folge von messbaren Funktionen
eine Folge von messbaren Funktionen 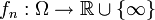 .
.
Weiter konvergiere die Folge 
 -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f, und die Folge
-messbare Funktion f, und die Folge  werde von einer Funktion
werde von einer Funktion 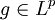 majorisiert, d.h., für alle
majorisiert, d.h., für alle  gilt
gilt 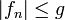
 -fast überall.
-fast überall.
Dann sind alle fn und auch f in Lp und es gilt: Die Folge  konvergiert gegen f im Sinne von Lp, d.h.
konvergiert gegen f im Sinne von Lp, d.h.
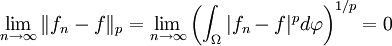 .
.
Beweisskizze: Anwendung des Originalsatzes auf die Funktionenfolge hn = | fn − f | p mit der Majorante (2g)p.
Siehe auch
Literatur
- Elliott H. Lieb & Michael Loss: Analysis, Second Edition, ISBN 0-8218-2783-9
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Satz von der majorisierten Konvergenz — Der Satz von der majorisierten Konvergenz (auch Satz von der majorisierenden Konvergenz, Satz von der dominierten Konvergenz oder Satz von Lebesgue) ist eine zentrale Grenzwertaussage in der Maß und Integrationstheorie und geht auf den… … Deutsch Wikipedia
Satz von Lebesgue — Der Satz von der majorisierten Konvergenz (auch Satz von der majorisierenden Konvergenz, Satz von der dominierten Konvergenz oder Satz von Lebesgue) ist eine zentrale Grenzwertaussage in der Maß und Integrationstheorie und geht auf den… … Deutsch Wikipedia
Geschichte der Stochastik — Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung … Deutsch Wikipedia
Geschichte der Wahrscheinlichkeitstheorie — Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung … Deutsch Wikipedia
Geschichte der Wahrscheinlichkeitsrechnung — Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung … Deutsch Wikipedia
Integrable Funktion — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Integrierbare Funktion — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgue-integrierbar — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgueintegral — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgue-Integral — Illustration der Grenzwertbildung beim Riemann Integral (blau) und beim Lebesgue Integral (rot) Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen… … Deutsch Wikipedia
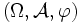 ein Maßraum und sei
ein Maßraum und sei  eine Folge von
eine Folge von  -messbaren Funktionen
-messbaren Funktionen 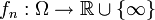 .
. konvergiere
konvergiere  -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f. Ferner werde die Folge
-messbare Funktion f. Ferner werde die Folge  von einer
von einer  -integrierbaren Funktion
-integrierbaren Funktion 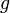 auf
auf 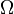 majorisiert, sprich für alle
majorisiert, sprich für alle  gelte
gelte 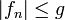
 -fast überall.
-fast überall.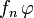 -integrierbar und es gilt:
-integrierbar und es gilt: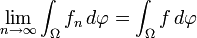 sowie
sowie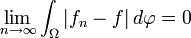
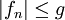 kann nicht verzichtet werden. Als Beispiel dient die Folge
kann nicht verzichtet werden. Als Beispiel dient die Folge 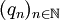 , definiert durch
, definiert durch ![q_n : [0,1] \rightarrow\mathbb{R}, q_n := n \chi_{[0,{1\over n}]}](/pictures/dewiki/97/a5c7bd967c41f8f56061fc6383142373.png) , worin
, worin ![\chi_{[0,{1\over n}]}](/pictures/dewiki/50/21c2f47dc5d6425b6633c0bd46a2bed5.png) die Indikatorfunktion auf
die Indikatorfunktion auf ![[0,{1 \over n}]](/pictures/dewiki/102/f709a04a682386d1aa36cf01125f791d.png) bezeichne.
bezeichne.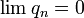 fast überall, aber dennoch ist
fast überall, aber dennoch ist ![\lim \int_{[0,1]} q_n = \lim 1 = 1 \ne 0 = \int_{[0,1]} 0 = \int_{[0,1]} \lim q_n](/pictures/dewiki/99/ccf495a5236cf75e90fc7aa230e5048a.png) .
.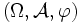 ein Maßraum,
ein Maßraum, 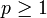 eine reelle Zahl und sei
eine reelle Zahl und sei  eine Folge von messbaren Funktionen
eine Folge von messbaren Funktionen 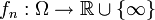 .
.
 -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f, und die Folge
-messbare Funktion f, und die Folge  werde von einer Funktion
werde von einer Funktion 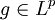 majorisiert, d.h., für alle
majorisiert, d.h., für alle  gilt
gilt 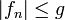
 -fast überall.
-fast überall. konvergiert gegen f im Sinne von Lp, d.h.
konvergiert gegen f im Sinne von Lp, d.h.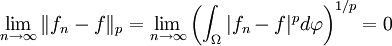 .
.