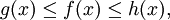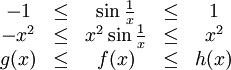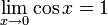- Satz von den zwei Polizisten
-
Der Einschnürungssatz (auch Dreifolgensatz oder englisch sandwich theorem) ist in der Analysis ein Satz über den Grenzwert einer Funktion. Gemäß dem Einschnürungssatz strebt eine Funktion, die von oben und unten durch zwei gegen denselben Wert strebenden Funktionen "eingezwängt" wird, auch gegen diesen Wert.
Der Einschnürungssatz wird typischerweise dazu verwendet, einen Grenzwert einer Funktion nachzuweisen, indem man die Funktion mit zwei anderen vergleicht, deren Grenzwerte bekannt oder einfach zu bestimmen sind. Es wurde geometrisch schon von den Mathematikern Archimedes und Eudoxus verwendet, um die Kreiszahl π zu berechnen. Die moderne Formulierung des Satzes stammt ursprünglich von Carl Friedrich Gauß.
Inhaltsverzeichnis
Formale Beschreibung
Es sei I ein Intervall, das einen Wert a enthält. Es seien f, g und h auf
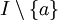 definierte Funktionen. Wenn für jedes
definierte Funktionen. Wenn für jedes 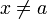 aus I gilt
aus I giltsowie
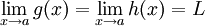 ,
,
dann ist
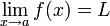 .
.a muss nicht inmitten von I liegen. Ist a Randpunkt von I, so handelt es sich bei obigen Grenzwerten um links- bzw. rechtsseitige. Ähnliches gilt auch für unendliche Intervalle: Ist beispielsweise
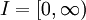 , so gilt der Satz auch für die Grenzwertuntersuchung
, so gilt der Satz auch für die Grenzwertuntersuchung 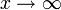 .
.Der Beweis ergibt sich unmittelbar aus der ε-δ-Definition des Grenzwertes, weil mit g(x) und h(x) auch stets f(x) in einer ε-Umgebung von L liegt.
Beispiele und Anwendungen
Die folgenden Beispiele zeigen, wie der Satz praktisch angewendet wird.
Beispiel 1
Man betrachte
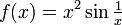 , das auf ganz
, das auf ganz  außer für x = 0 definiert ist. Den Grenzwert für
außer für x = 0 definiert ist. Den Grenzwert für 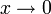 auf konventionelle Art zu berechnen fällt schwer: Eine direkte Substitution schlägt fehl, weil die Funktion bei x = 0 nicht definiert ist (geschweige denn stetig), und die Regel von L'Hospital kann auch nicht angewendet werden, da
auf konventionelle Art zu berechnen fällt schwer: Eine direkte Substitution schlägt fehl, weil die Funktion bei x = 0 nicht definiert ist (geschweige denn stetig), und die Regel von L'Hospital kann auch nicht angewendet werden, da 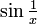 überall oszilliert und keinen Grenzwert hat. Mit passenden oberen und unteren Schrankenfunktionen lässt sich jedoch der Einschnürungssatz anwenden.
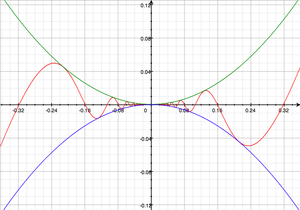
überall oszilliert und keinen Grenzwert hat. Mit passenden oberen und unteren Schrankenfunktionen lässt sich jedoch der Einschnürungssatz anwenden.Da die Sinusfunktion beträgsmäßig durch 1 begrenzt ist, ist x2 betragsmäßig eine passende Schranke für f. In anderen Worten gilt mit g(x) = − x2 und h(x) = x2:
g und h sind Polynomfunktionen und deshalb stetig, daher gilt
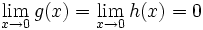 .
.
Aus dem Sandwich-Theorem folgt nun
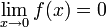 .
.
Beispiel 2
Das obige Beispiel ist eine spezielle Anwendung eines häufig auftretenden allgemeinen Falles. Angenommen, wir wollen zeigen, dass
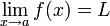 .
.
Es ist dann ausreichend, eine Funktion h zu finden, die auf einem a enthaltenden Intervall I definiert ist (außer möglicherweise bei a), für die gilt
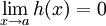 ,
,
und außerdem für alle
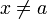 aus I gilt
aus I gilt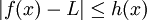 .
.
In Worten gesprochen heißt das, dass der Fehler zwischen f(x) und L beliebig klein gemacht werden kann, wählt man x nahe genug an a. Diese Bedingungen sind ausreichend, da die Betragsfunktion überall nicht negativ ist, so dass wir
- g(x) = 0 für alle x
wählen können und den Einschnürungssatz anwenden können. Da nun
- für
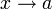 gilt
gilt 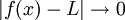 ,
,
gilt auch
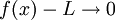 und damit
und damit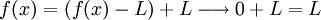 .
.
Beispiel 3
Durch elementargeometrische Überlegungen lässt sich zeigen, dass
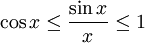 .
.
Wegen
folgt mit dem Einschnürungssatz
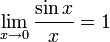 .
.
Dieser Grenzwert ist bei der Bestimmung der Ableitungsfunktion des Sinus behilflich.
Weblinks
- Joseph M. Ling (2001): Examples on Limits of Functions: The Squeeze Theorem
- Dr. C. Sean Bohun: The Squeeze Theorem
Wikimedia Foundation.