- Satz von Lebesgue
-
Der Satz von der majorisierten Konvergenz (auch Satz von der majorisierenden Konvergenz, Satz von der dominierten Konvergenz oder Satz von Lebesgue) ist eine zentrale Grenzwertaussage in der Maß- und Integrationstheorie und geht auf den französischen Mathematiker Henri Léon Lebesgue zurück.
Der Satz liefert ein Entscheidungskriterium für die Vertauschbarkeit von Integral- und Grenzwertbildung.
Inhaltsverzeichnis
Der Satz formal in seiner allgemeinsten Form
Sei
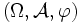 ein Maßraum und sei
ein Maßraum und sei  eine Folge von
eine Folge von  -messbaren Funktionen
-messbaren Funktionen 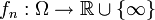 .
.Die Folge
 konvergiere
konvergiere  -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f. Ferner werde die Folge
-messbare Funktion f. Ferner werde die Folge  von einer
von einer  -integrierbaren Funktion
-integrierbaren Funktion 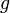 auf
auf 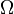 majorisiert, sprich für alle
majorisiert, sprich für alle  gelte
gelte 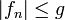
 -fast überall.
-fast überall.Dann sind f und alle
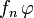 -integrierbar und es gilt:
-integrierbar und es gilt: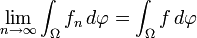 sowie
sowie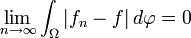
Bemerkung zur Voraussetzung
Auf die Voraussetzung der Majorisierbarkeit
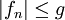 kann nicht verzichtet werden. Als Beispiel dient die Folge
kann nicht verzichtet werden. Als Beispiel dient die Folge 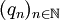 , definiert durch
, definiert durch ![q_n : [0,1] \rightarrow\mathbb{R}, q_n := n \chi_{[0,{1\over n}]}](/pictures/dewiki/97/a5c7bd967c41f8f56061fc6383142373.png) , worin
, worin ![\chi_{[0,{1\over n}]}](/pictures/dewiki/50/21c2f47dc5d6425b6633c0bd46a2bed5.png) die Indikatorfunktion auf
die Indikatorfunktion auf ![[0,{1 \over n}]](/pictures/dewiki/102/f709a04a682386d1aa36cf01125f791d.png) bezeichne.
bezeichne.Es gilt
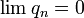 fast überall, aber dennoch ist
fast überall, aber dennoch ist ![\lim \int_{[0,1]} q_n = \lim 1 = 1 \ne 0 = \int_{[0,1]} 0 = \int_{[0,1]} \lim q_n](/pictures/dewiki/99/ccf495a5236cf75e90fc7aa230e5048a.png) .
.Majorisierte Konvergenz in Lp-Räumen (Folgerung)
Sei
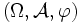 ein Maßraum,
ein Maßraum, 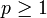 eine reelle Zahl und sei
eine reelle Zahl und sei  eine Folge von messbaren Funktionen
eine Folge von messbaren Funktionen 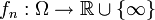 .
.Weiter konvergiere die Folge

 -fast überall gegen eine
-fast überall gegen eine  -messbare Funktion f, und die Folge
-messbare Funktion f, und die Folge  werde von einer Funktion
werde von einer Funktion 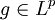 majorisiert, d.h., für alle
majorisiert, d.h., für alle  gilt
gilt 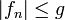
 -fast überall.
-fast überall.Dann sind alle fn und auch f in Lp und es gilt: Die Folge
 konvergiert gegen f im Sinne von Lp, d.h.
konvergiert gegen f im Sinne von Lp, d.h.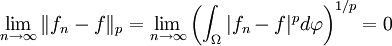 .
.
Beweisskizze: Anwendung des Originalsatzes auf die Funktionenfolge hn = | fn − f | p mit der Majorante (2g)p.
Siehe auch
Literatur
- Elliott H. Lieb & Michael Loss: Analysis, Second Edition, ISBN 0-8218-2783-9
Wikimedia Foundation.
