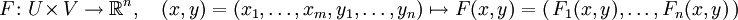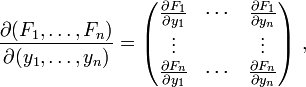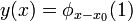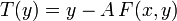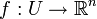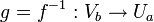Satz von der inversen Funktion

Der Satz von der impliziten Funktion ist einer der wichtigsten Sätze in der Analysis. Er beinhaltet ein relativ einfaches Kriterium, wann man eine implizite Gleichung oder ein Gleichungssystem (lokal) eindeutig auflösen kann.

Begriffsbestimmung

Eine implizit definierte Funktion (kurz implizite Funktion) ist eine Funktion, die nicht in der „einfachen“ Zuordnungsvorschrift y = f(x) gegeben, sondern deren Funktionswerte implizit durch eine Gleichung F(x,y) = 0 definiert sind. Dabei ist F eine vektorwertige Funktion, die genauso viele Einzelfunktionen enthält, wie y Komponenten hat. Wird x fixiert, so ergibt sich ein Gleichungssystem in y mit genauso vielen Gleichungen wie Unbekannten. Der Satz über die implizite Funktion besagt nun, unter welchen Voraussetzungen die Aussage gilt:

Wenn eine Lösung y₀ für einen Parametervektor x₀ bekannt ist, dann kann für jeden Parametervektor 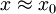$x\approx x_0$ in einer kleinen Umgebung von x₀ auch immer eine eindeutig bestimmte Lösung 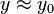$y\approx y_0$ des Gleichungssystems F(x,y) = 0 gefunden werden, die in einer Umgebung der ursprünglichen Lösung y₀ liegt.

Diese Aussage des Satzes erlaubt nun, eine Funktion zu definieren, die jedem Parametervektor 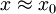$x\approx x_0$ gerade den Lösungsvektor 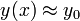$y(x)\approx y_0$ zuordnet, so dass diese Funktion auf ihrem Definitionsbereich die Gleichung F(x,y(x)) = 0 erfüllt. Der Satz von der impliziten Funktion stellt zudem sicher, dass diese Zuordnung 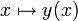$x \mapsto y(x)$ unter gewissen Bedingungen und Einschränkungen an F, x und y wohldefiniert ist, insbesondere, dass sie eindeutig ist.

Motivierendes Beispiel

Ein Kreis mit Radius 1 in der Ebene wird durch die Menge aller Zahlen x und y beschrieben, die x² + y² − 1 = 0 erfüllen. Diese Gleichung kann man nach y auflösen, und man erhält 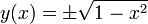$y(x) = \pm \sqrt{1 - x^2}$. Die letzte Form ist jetzt eine explizite Definition (y(x) = ...), während die ursprüngliche Kreisgleichung eine implizite Definition der gleichen Funktion war.

Aus dem Beispiel sieht man auch die Probleme der expliziten Definition: Es ist nicht immer möglich, die Gleichung aufzulösen, bzw. die Auflösung ist nicht eindeutig - man muss im Beispiel beide Vorzeichen wählen um den gesamten Kreisrand zu beschreiben.

Der Satz von der impliziten Funktion gilt ebenso für Gleichungssysteme: Hat man n implizite Gleichungen in m Variablen (m>n), dann ist zu erwarten, dass man nach n Variablen y_i auflösen kann, die sich dann als Funktionen der restlichen m − n Variablen ausdrücken lassen.

Formulierung des Satzes

Der Satz von der impliziten Funktion gibt ein Kriterium an, wann man die Gleichung in einer Umgebung auflösen kann.

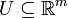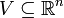Seien $U \subseteq \mathbb{R}^m$ und $V \subseteq \mathbb{R}^n$ offene Teilmengen und

$F\colon U \times\, V \to \mathbb{R}^n,\quad (x,y)=(x_1,\dots,x_m,y_1,\dots,y_n) \mapsto F(x,y)=(\,F_1(x,y),\dots,F_n(x,y)\,)$

eine stetig differenzierbare Abbildung; und 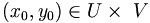$(x_0, y_0) \in U \times\ V$ erfülle die Gleichung F(x₀,y₀) = 0.

Falls die quadratische Teilmatrix der Jacobi-Matrix, die die partiellen Ableitungen von F nach den y-Variablen enthält,

$\frac{\partial (F_1, \ldots , F_n)}{\partial(y_1, \ldots , y_n)} = \begin{pmatrix}\frac{\partial F_1}{\partial y_1} & \cdots & \frac{\partial F_1}{\partial y_n} \\ \vdots & & \vdots \\ \frac{\partial F_n}{\partial y_1} & \cdots & \frac{\partial F_n}{\partial y_n} \end{pmatrix}\ ,$

im Punkt (x₀,y₀) invertierbar ist, existieren offene Umgebungen U₀ von x_o und V_o von y_o sowie eine eindeutige stetig differenzierbare Abbildung

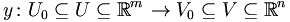$y\colon {U_0} \subseteq {U} \subseteq {\mathbb{R}^m} \to {V_0} \subseteq {V} \subseteq {\mathbb{R}^n}$, mit y(x₀) = y₀, so dass

F(x,y(x)) = 0

für alle 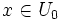$x \in U_0$ gilt.

Diskussion des Beispiels

Man wende nun diesen Satz auf das anfangs gegebene Beispiel der Kreisgleichung an: Dazu sind die partiellen Ableitungen nach den y-Variablen zu betrachten. (In diesem Fall ist n = 1, also ergibt das eine 1×1 Matrix, bzw. einfach eine Zahl): Die partielle Ableitung der Funktion F(x,y) = x² + y² − 1 nach y ergibt 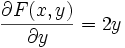$\frac{\partial F(x,y)}{\partial y} = 2 y$. Diese Zahl ist invertierbar genau dann, wenn 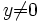$y \not= 0$. Damit folgert man mit Hilfe des Satzes, dass diese Gleichung nach y auflösbar ist, wenn 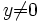$y \not= 0$. Der Fall y = 0 tritt nur in den Punkten x = − 1 oder x = 1 auf. Dies sind also die Problempunkte. Tatsächlich sieht man, dass die Formel 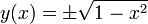$y(x) = \pm \sqrt{1 - x^2}$ sich genau in diesen Problempunkten in eine positive und negative Lösung verzweigt. In allen anderen Punkten ist die Auflösung lokal eindeutig.

Beweisansatz

Der klassische Ansatz betrachtet zur Lösung der Gleichung F(x,y) = 0 das Anfangswertproblem der gewöhnlichen Differentialgleichung

$\phi_v'(t)=-G(x_0+tv,\phi_v(t)) \;\text{ mit }\; G(x,y)=\left(\tfrac{\partial F}{\partial y}(x,y)\right)^{-1}\tfrac{\partial F}{\partial x}(x,y) \;\text{ und }\; \phi_v(0)=y_0$.

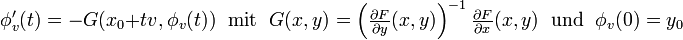Da 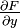$\tfrac{\partial F}{\partial y}$ in (x₀,y₀) invertierbar ist, ist dies auch in einer kleinen Umgebung der Fall, d.h. für kleine Vektoren v existiert die Differentialgleichung und ihre Lösung für alle $t\in [0,1]$. Die Lösung der impliziten Gleichung ist nun durch

$y(x)=\phi_{x-x_0}(1)$

gegeben, die oben angegebenen Eigenschaften dieser Lösung ergeben sich aus den Eigenschaften der Lösungen parameterabhängiger Differentialgleichungen.

Der moderne Ansatz formuliert das Gleichungssystem F(x,y) = 0 mit Hilfe des vereinfachten Newton-Verfahrens als Fixpunktproblem und wendet darauf den Fixpunktsatz von Banach an. Für die dazugehörige Fixpunktabbildung wird die Inverse A der Teilmatrix 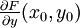$\tfrac{\partial F}{\partial y}(x_0,y_0)$ der Jacobi-Matrix von F im vorgegebenen Lösungspunkt (x₀,y₀) gebildet. Zu der Abbildung

$T(y)=y-A\,F(x,y)$

kann man nun zeigen, dass für Parametervektoren x nahe x₀ diese Abbildung auf einer Umgebung von y₀ kontraktiv ist. Dies folgt daraus, dass T stetig differenzierbar ist und 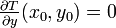$\tfrac{\partial T}{\partial y}(x_0,y_0)=0$ gilt.

Zusammenfassung

Der Vorteil des Satzes ist, dass man die explizite Funktion y(x) gar nicht kennen muss, und trotzdem eine Aussage über deren Existenz und Eindeutigkeit folgern kann. In vielen Fällen ist die Gleichung für y(x) auch gar nicht mit Formeln lösbar, sondern nur mit numerischen Verfahren. Interessant ist, dass die Konvergenz solcher Verfahren meist gleiche oder ähnliche Voraussetzung wie der Satz von der impliziten Funktion (Matrix der y-Ableitungen muss invertierbar sein) erfordert.

Eine weitere wertvolle Schlussfolgerung des Satzes ist, dass die Funktion y(x) differenzierbar ist, falls F(x,y) es ist, was bei Anwendung des Satzes über implizite Funktionen vorausgesetzt wird. Die Ableitung kann sogar explizit angegeben werden:

$\frac{\partial y \left(x \right)}{\partial x} = - \left( \frac{\partial F \big(x,y(x)\big)}{\partial y} \right)^{-1} \cdot \frac{\partial F \big(x,y(x)\big)}{\partial x}$.

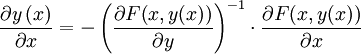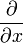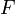Ist x ein Vektor, so ist die partielle Ableitung $\frac{\partial}{\partial x}$ als Jacobimatrix aus den Komponentenableitungen $x_1, \dots x_n$ zu verstehen, analog für y. Eine ähnliche Folgerung gilt für höhere Ableitungen. Ersetzt man die Voraussetzung "$F\$ ist stetig differenzierbar", durch "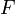$F\$ ist k-mal stetig differenzierbar" (oder beliebig oft oder analytisch), kann man folgern, dass y(x) k-mal differenzierbar (bzw. beliebig oft bzw. analytisch) ist.

Satz von der Umkehrabbildung

Ein nützliches Korollar zum Satz von der impliziten Funktion ist der Satz von der Umkehrabbildung. Er gibt eine Antwort auf die Frage, wann man eine Umkehrfunktion finden kann:

Sei 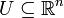$U \subseteq \mathbb{R}^n$ offen und

$f : U \to \mathbb{R}^n$

eine stetig differenzierbare Abbildung. Sei 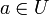$a \in U$ und b: = f(a). Die Jacobi-Matrix Df(a) sei invertierbar. Dann gibt es eine offene Umgebung 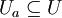$U_a \subseteq U$ von a und eine offene Umgebung V_b von b, so dass f die Menge U_a bijektiv auf V_b abbildet und die Umkehrfunktion

$g = f^{-1} : V_b \to U_a$

stetig differenzierbar ist. Es gilt Dg(b) = (Df(a)) ^{− 1}.

Literatur

• Herbert Amann, Joachim Escher: Analysis II. Birkhäuser, Basel, 1999, ISBN 3-7643-6133-6, S. 230 ff.
• Otto Forster: Analysis 2. 7. Auflage. Vieweg, Wiesbaden 2006, ISBN 3-8348-0250-6, I.8 Implizite Funktionen, S. 86 - 99.