- Weierstraßsche elliptische Funktion
-
Im mathematischen Teilgebiet der Funktionentheorie sind elliptische Funktionen doppeltperiodische meromorphe Funktionen. „Doppeltperiodisch“ bedeutet, dass es zwei komplexe Zahlen ω1,ω2 gibt, die keine reellen Vielfachen voneinander sind, so dass die beiden Funktionalgleichungen
- f(z + ω1) = f(z) und f(z + ω2) = f(z)
für alle z erfüllt sind. "Meromorph" bedeutet, dass die Funktion bis auf Pole überall regulär (= analytisch = holomorph) ist.
Inhaltsverzeichnis
Das Periodengitter und die Grundmasche
Sind f und ω1,ω2 wie oben, so gilt auch
- f(z + γ) = f(z)
für jedes γ = μω1 + λω2 mit ganzen Zahlen μ,λ. Die abelsche Gruppe
heißt das Periodengitter. Es ist ein vollständiges Gitter in
 .
.Das von ω1 und ω2 aufgespannte Parallelogramm
heißt Grundmasche des Gitters.
Einfache Eigenschaften
- Eine holomorphe elliptische Funktion ist konstant: Sie ist ganz, und sie ist beschränkt, da sie auf der Grundmasche bereits alle ihre Werte annimmt und die Grundmasche kompakt ist. Nach dem Satz von Liouville ist sie also konstant.
- Eine elliptische Funktion kann nicht genau einen einfachen Pol in der Grundmasche haben, da das Integral über den Rand der Grundmasche aufgrund der Periodizität verschwindet; dies schließt nach der Cauchyschen Integralformel einen einfachen Pol aus.
- Die entsprechende Aussage gilt auch für genau eine einfache Nullstelle, da mit f auch 1 / f eine elliptische Funktion ist.
Die Weierstraßsche ℘-Funktion
Zu einem Periodengitter Γ existiert stets eine nicht konstante elliptische Funktion, die Weierstraßsche ℘-Funktion:
Im wesentlichen wird also 1 / z2 durch Translationen zu einer Γ-invarianten Funktion gemacht; die Summanden − 1 / γ2 dienen lediglich dazu, die Reihe konvergent zu machen.
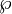 ist eine gerade elliptische Funktion, d. h.
ist eine gerade elliptische Funktion, d. h. 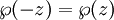 . Ihre Ableitung
. Ihre Ableitungist eine ungerade elliptische Funktion, d.h.
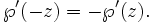
Das zentrale Resultat der Theorie der elliptischen Funktionen ist die folgende Aussage: Jede elliptische Funktion zum Periodengitter Γ lässt sich als rationale Funktion in
 und
und 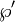 schreiben. Jede Relation zwischen
schreiben. Jede Relation zwischen 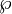 und
und 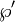 folgt aus der Differentialgleichung der
folgt aus der Differentialgleichung der 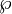 -Funktion
-FunktionDabei sind g2(Γ),g3(Γ) Konstanten, die von Γ abhängen, genauer sind g2(Γ) = 60G4(Γ) und g3(Γ) = 140G6(Γ) Eisensteinreihen zum Gitter Γ. In algebraischer Sprache bedeutet dieser Satz: Der Körper der elliptischen Funktionen zum Periodengitter Γ ist isomorph zum Körper
Unter diesem Isomorphismus wird
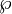 auf X und
auf X und 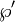 auf Y abgebildet.
auf Y abgebildet.Beziehung zu Ellipsen und elliptischen Integralen
Der Name der elliptischen Funktionen weist darauf hin, dass sie zuerst bei der Berechnung des Umfangs von Ellipsen verwendet wurden. Eine weitere Anwendung ist die Berechnung der Schwingungsdauer eines Pendels.
Die elliptischen Funktionen sind Umkehrfunktionen der elliptischen Integrale.
Verallgemeinerungen der elliptischen Funktionen sind die hyperelliptischen Funktionen.
Zur Geschichte der elliptischen Funktionen
Bald nach der Erfindung der Infinitesimalrechnung stießen Mathematiker auf Probleme, bei denen Integrale auftraten, in denen die Quadratwurzeln aus Polynomen 3. und 4. Grades auftraten. Man erkannte, dass sie sich nicht in geschlossener Form durch die bis dahin gebräuchlichen Funktionen ausdrücken ließen. Euler (1707–1783) brachte sie 1766 in einen Zusammenhang miteinander mit Hilfe eines Satzes, nach dem er die Summe gewisser derartiger Integrale wieder als ein Integral derselben Art darstellen konnte. Er hob hervor, dass man diese Integrale ebenso wie die zyklometrischen Funktionen und die Logarithmusfunktion als Symbole in die Mathematik einführen könne.
Seine Ideen wurden – abgesehen von einer Bemerkung Landens – erst 1786 durch Legendre (1752–1833) in seinem Mémoire sur les intégrations par d'arcs d'ellipse weiter verfolgt. Legendre hat sich von da an immer wieder mit dieser Art von Integralen beschäftigt und nannte sie „elliptische Funktionen“. Von Legendres Arbeiten sind noch zu erwähnen: Mémoire sur les transcendantes elliptiques (Paris 1793), Exercices etc. (Paris 1811–1819), Traité des fonctions elliptiques (Paris 1825–1828). Legendre führte die elliptischen Funktionen auf drei feste Formen – Gattungen – zurück, wodurch er sich den seinerzeit sehr schwierigen Zugang zu ihrer Untersuchung wesentlich erleichterte. Seine Arbeiten blieben jedoch bis 1826 völlig unbeachtet.
Erst von da an nahmen die beiden Mathematiker Abel (1802–1829) und Jacobi (1804–1851) diese Untersuchungen wieder auf und kamen schnell zu ungeahnten neuen Erkenntnissen. Zunächst kehrten sie das Problem um, indem sie die veränderlich gedachte obere Grenze des Integrals als Funktion des Integralwertes auffassten, also die zu den elliptischen Integralen inversen Funktionen betrachteten. Diese inversen Funktionen heißen nach einem Vorschlag Jacobis von 1829 jetzt elliptische Funktionen. Die Arbeiten Jacobis und Abels finden sich in Crelles Journal von 1826 an. Außerdem sind Jacobis Fundamenta nova theoriae functionum ellipticarum (Königsberg 1829) zu nennen. Jacobi bewies 1835, dass die eindeutigen Funktionen einer Veränderlichen höchstens zwei unabhängige Perioden haben. Die elliptischen Funktionen haben genau zwei. Das von Euler in sehr spezieller Form gefundene Additionstheorem wurde in seiner allgemeinen Form 1829 von Abel ausgesprochen und bewiesen. Gauß hatte, wie er selbst bemerkte und wie sich auch hat nachweisen lassen, schon dreißig Jahre vorher viele der Eigenschaften der elliptischen Funktionen gefunden, aber nichts darüber publiziert.
Die weitere Entwicklung hat zu den hyperelliptischen Funktionen, den Abelschen Funktionen und den Modulfunktionen geführt.
Literatur
- Hurwitz, Courant: Funktionentheorie. 1.–4. Aufl., Springer Verlag
- Durege: Theorie der Elliptischen Funktionen. 2. Aufl., BGTeubner, 1868
- Francesco Tricomi: Elliptische Funktionen. Leipzig 1948
- Burkhardt: Elliptische Funktionen. Veit & Comp. 1899
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Aufl., Springer-Verlag, Berlin 2006, ISBN 3-540-31764-3
- Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen., 2. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49324-2
Siehe auch
Wikimedia Foundation.

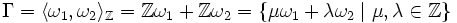
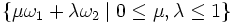
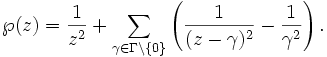
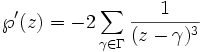
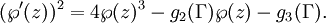
![\mathbb C(X)[Y]/(Y^2-4X^3+g_2X+g_3).](/pictures/dewiki/54/61ffd97370c74dfe510a00697bce1841.png)

![\scriptstyle\Gamma = [1,e^{\pi i/3}]](/pictures/dewiki/99/c5ab25f796ff7f80d6736cdd4efbaf39.png)
![\scriptstyle[-2,2]\times[-1.125,1.125] i](/pictures/dewiki/52/4fadd44049bb68e148676b16d551e7ad.png) .
. 

![\scriptstyle\Gamma = [1, \frac 12+\frac i3]](/pictures/dewiki/97/a30672710e894bcf5b020ba3d616766b.png)