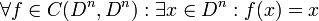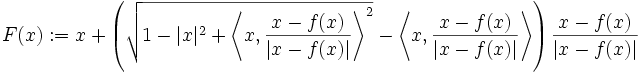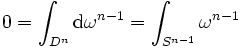Brouwerscher Fixpunktsatz

Der Fixpunktsatz von Brouwer ist eine Aussage aus der Mathematik. Er ist benannt nach dem niederländischen Mathematiker Luitzen Egbertus Jan Brouwer.

Der Fixpunktsatz von Brouwer besagt, dass die Vollkugel Dⁿ die Fixpunkteigenschaft hat, also jede stetige Abbildung f der n-dimensionalen Vollkugel in die n-dimensionale Vollkugel einen Fixpunkt besitzt. In Formeln:

$\forall f \in C(D^{n},D^{n}): \exists x \in D^n : f(x) = x$

Der Satz bietet also eine Existenzaussage für die Lösung reeller, nichtlinearer Gleichungssysteme.

Beweisidee

Mittels des Approximationssatzes von Stone-Weierstraß kann man sich auf 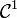$\mathcal C^1$-Funktionen beschränken.

Nun nimmt man an, f habe keinen Fixpunkt, also müsste die glatte Abbildung 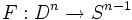$F: D^n\to S^{n-1}$, die jedem Punkt in der Vollkugel einen Schnittpunkt der Gerade durch x und f(x) mit der Sphäre zuordnet:

$F(x):=x + \left( \sqrt{1-|x|^2 + \left\langle x,\frac{x-f(x)}{|x-f(x)|} \right\rangle^2 } - \left\langle x, \frac{x-f(x)}{|x-f(x)|} \right\rangle \right) \frac{x-f(x)}{|x-f(x)|}$

Illustration von F in D²

wohldefiniert sein. F ist eine Retraktion, d.h. F(x) = x für $x\in S^{n-1}.$

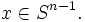
Dies führt man auf einen Widerspruch,indem man zunächst zeigt, dass für 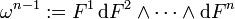$\omega^{n-1}:= F^1\, \mathrm dF^2\wedge\cdots\wedge \mathrm dF^n$ gilt: dω^{n − 1} = 0. Dies sieht man leicht ein, da die Determinante der Jacobi-Matrix von F nach dem Satz von der inversen Funktion 0 sein muss.

Also gilt:

$0 = \int_{D^n} \mathrm d\omega^{n-1} = \int_{S^{n-1}} \omega^{n-1}$

nach dem Satz von Stokes. Auf der Sphäre ist F aber die Identität. Damit gilt also (wieder nach dem Satz von Stokes):

$= \int_{S^{n-1}} x_1 \mathrm dx^2 \wedge \cdots \wedge \mathrm dx^n = vol (D^n) \neq 0$.

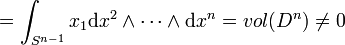Literatur

• Harro Heuser: Lehrbuch der Analysis - Teil 2, 5. Auflage, Teubner 1990, ISBN 3-519-42222-0, S.593

Weblinks

• Eric W. Weisstein: Brouwer Fixed Point Theorem auf MathWorld (englisch)
• Skript zur Mengentheoretische Topologie (im PDF-Format, deutsch)