Skolemformel

Skolemform ist ein Begriff der Prädikatenlogik und bezeichnet eine prädikatenlogische Formel, die sich in einer Normalform nach Albert Thoralf Skolem befindet. Für Formeln in Skolemform existiert ein berechenbarer Test auf Erfüllbarkeit. Dies ist nützlich, da jede Formelmenge X genau dann erfüllbar ist, wenn ihre Skolemform erfüllbar ist. Des Weiteren ist die Skolemform ein hilfreicher Zwischenschritt, wenn man eine Formel in Klausel-Normalform umformen will. Sie wird auch als Zwischenergebnis benötigt, wenn man ein Herbrand-Universum erzeugen will.

In der Skolemform sind keine Existenzquantoren ( 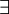$\exists{}$ ) mehr enthalten. Variablen, die an Existenzquantoren gebunden waren, werden durch neue Funktionssymbole ersetzt. Als Argumente bekommen die neuen Funktionssymbole die Variablen der Allquantoren ( 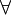$\forall{}$ ), die vor dem entfernten Existenzquantor standen.

Algorithmus zum Erzeugen der Skolemform

Man erhält eine Formel nach Skolem, wenn man auf eine bereinigte, pränexe Formel F folgende Umformungen anwendet:

Solange F einen Existenzquantor enthält:

{

F habe die Form:

$F=\forall y_1\forall y_2...\forall y_n \exists xG$

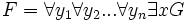
Setze:

$F := \forall y_1\forall y_2...\forall y_nG\left[x/f\left(y_1,...,y_n\right)\right]$

Dabei sei f ein in F noch nicht vorkommendes n-stelliges Funktionssysmbol. Die Stelligkeit der Funktion wird dabei bestimmt durch die Allquantoren vor dem zu skolemisierenden Symbol, wobei die Funktion jeweils auf den nächsten vorhergehenden Allquantor zu beziehen ist. Nullstellige Funktionssymbole sind Konstanten.

}

Hinweis: $G\left[x/w\right]$ steht hier für die Formel G in der x durch w ersetzt wurde. f heißt Skolemfunktion, im Fall n = 0 Skolemkonstante.

Als Ergebnis erhält man die Formel F in Skolemform. Andere Bezeichnungen sind Skolemisierung von F oder auch Skolemsche Normalform. Zu beachten ist, dass bei der beschriebenen Umformung nicht notwendigerweise die logische Äquivalenz erhalten bleibt. Sie erhält zwar die Erfüllbarkeit der Formel und ist somit erfüllbarkeitsäquivalent, ist aber nicht modellerhaltend. Dies bedeutet, dass eine Interpretation, welche die ursprüngliche Formel erfüllt, nicht notwendigerweise auch die skolemisierte Formel erfüllt (siehe hierzu auch Logik), was aufgrund des neu zu interpretierenden Funktionssymbols auch nicht verwunderlich ist.

Beispiel

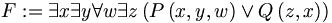$F:=\exists x\exists y\forall w\exists z\left(P\left(x,y,w\right)\vee Q\left(z,x\right)\right)$ ist in Bereinigter Pränexform (BPF).

Durch Anwendung des oben aufgeführten Algorithmus erhält man:

• Im ersten Schritt wird 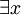$\exists{x}$ durch die neu eingeführte nullstellige Funktion a ersetzt:

$F':=\exists y\forall w\exists z\left(P\left(a,y,w\right)\vee Q\left(z,a\right)\right)$

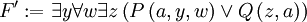
• b wird danach als Ersetzung für 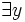$\exists{y}$ eingeführt:

$F'':=\forall w\exists z\left(P\left(a,b,w\right)\vee Q\left(z,a\right)\right)$

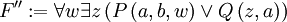
• Dann wird 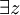$\exists{z}$ ersetzt. Dafür wird die 1-stellige Funktion f eingeführt. Sie erhält als Argument die per Allquantor gebundene Variable w, da der Allquantor vor dem Existenzquantor steht.

$F''':=\forall w\left(P\left(a, b, w\right)\vee Q\left(f\left(w\right), a\right)\right)$

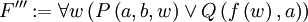
Nun liegt die Formel in Skolemform mit den Konstanten a, b und einem 1-stelligen Funktionssymbol f(w) vor.