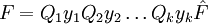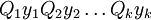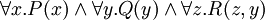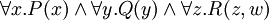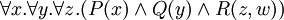- Pränex-Normalform
-
Die Pränexform ist eine mögliche Normalform, in der Aussagen der Prädikatenlogik dargestellt werden können. Sie wird unter anderem als Vorstufe zur Skolemform benötigt.
Eine Aussage in der Prädikatenlogik erster Stufe befindet sich in Pränexform, wenn alle Quantoren (Beschreibungen des Geltungsbereichs) außerhalb bzw. vor der eigentlichen Formel stehen. Enthält die Pränexform zusätzlich nur Konjunktion, Disjunktion und Negation (unmittelbar vor Atomen) als Junktoren, so wird sie auch als verneinungstechnische Normalform bezeichnet.
In der Prädikatenlogik gibt es zu jeder Formel eine logisch äquivalente Formel in Pränexform.
Eine Formel in bereinigter Pränexform ist erfüllbar, wenn Ihre Skolemform erfüllbar ist.
Mathematische Definition
Eine Formel F der Prädikatenlogik befindet sich in Pränexform, wenn Sie von der Form
ist, mit
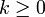 und
und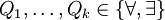 .
.
In
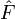 darf kein Quantor vorkommen.
darf kein Quantor vorkommen.Beispiel
Die Ausgangsformel lautet:
Es kommt die Variable y sowohl gebunden, als auch frei vor. Dies darf in der Pränexform aber nicht sein. Deshalb wird eine neue Variable eingeführt: w. Nach der Anpassung sieht das nun so aus:
Nun kommt jede Variable entweder gebunden oder frei vor und somit können wir die Quantoren alle nach vorn „ziehen“, was dann folgendermaßen ausschaut:
Wikimedia Foundation.