Stabil (Vektorbündel)

Der Slope μ(E) eines Vektorbündels E auf einer glatten projektiven Kurve ist der Quotient deg E/rk E aus Grad und Rang von E.

Ein Vektorbündel E heißt stabil, wenn für jedes nichttriviale Unterbündel F von E gilt: μ(F) < μ(E). E heißt semistabil, wenn die schwächere Bedingung μ(F) 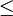$\leq$ μ(E) erfüllt ist. Geradenbündel, also Vektorbündel vom Rang eins, sind immer stabil.

Äquivalent dazu ist ein Vektorbündel E (semi-)stabil, wenn für jeden nichttrivialen Quotienten Q von E gilt: μ(Q) > μ(E) (bzw. μ(Q) 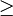$\geq$ μ(E)).

Dieser Begriff stammt von David Mumford und ist für die Konstruktion von Modulräumen entscheidend. Man kann nämlich nicht alle Vektorbündel durch ein geometrisches Objekt parametrisieren, sondern eben nur die (semi)stabilen. Diese Konstruktion verallgemeinert für größeren Rang die Konstruktion der Jacobischen Varietät einer Kurve.

Beispiele

• Auf dem P¹ sind nur die Geradenbündel stabil, semistabil sind Vektorbündel der Form O(n)^r für ganze Zahlen n und r ≥ 0. Dies beruht auf dem Satz von Grothendieck, dass jedes Vektorbündel auf der projektiven Gerade die direkte Summe von Geradenbündeln ist, und jedes Geradenbündel hat die Form O(n) mit einer ganzen Zahl n.

• Auf einer elliptischen Kurve sind die semistabilen Vektorbündel direkte Summen von unzerlegbaren Vektorbündeln vom gleichen slope. Die unzerlegbaren Vektorbündel sind nach der Klassifikation von Atiyah gegeben durch 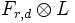$F_{r,d} \otimes L$. Hierbei bezeichnet L ein Geradenbündel.

• Für Kurven von höherem Geschlecht ist die Beschreibung der semistabilen Vektorbündel ungleich schwieriger.

Eigenschaften

• Sind E und F semistabil, und ist μ(E) > μ(F), so ist Hom(E,F) = 0, da das Bild einerseits Slope 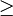$\geq$ μ(E), andererseits 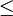$\leq$ μ(F) haben müsste.

Harder-Narasimhan-Filtrierung

Ist E ein beliebiges Vektorbündel, so besitzt E eine funktorielle, durch rationale Zahlen parametrisierte absteigende Filtrierung E^α, so dass die Filtrierungsquotienten semistabil mit Slope α sind. Sie wird dadurch gewonnen, dass man

• das größte semistabile Unterbündel F betrachtet (es ist gleichzeitig das größte derjenigen Unterbündel, die maximalen Slope besitzen)
• den Quotienten E/F bildet

und diesen Prozess wiederholt.