Vektorbündel

Vektorbündel (oder manchmal ausführlicher Vektorraumbündel) sind Familien von Vektorräumen, die durch die Punkte eines topologischen Raumes parametrisiert sind. Der Begriff der Basis einen Vektorraums kann auf diese speziellen Faserbündel verallgemeinert werden und heißt Rahmen.

Anschaulich besteht ein Vektorbündel aus je einem Vektorraum für jeden Punkt des Basisraumes. Da Vektorräume gleicher Dimension jedoch stets isomorph sind, liegt die wesentliche Information in den Beziehungen zwischen diesen Vektorräumen. Das bekannteste Beispiel für ein Vektorbündel ist das Tangentialbündel einer differenzierbaren Mannigfaltigkeit. Der Zusammenhang zwischen den verschiedenen Tangentialräumen, also den Vektorräumen zu den einzelnen Punkten, äußert sich beispielsweise in der Frage, ob ein Vektorfeld differenzierbar ist.

Die Frage, wie Vektorbündel auf einem Raum aussehen können, hängt eng mit globalen topologischen Eigenschaften des Raumes zusammen.

Definitionen

Vektorbündel

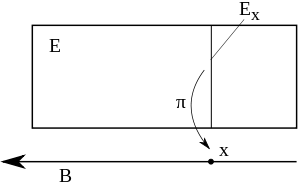Illustration des Vektorbündels (E,B,π). Hier ist der Totalraum $E=\R^2$ und der Basisraum $B=\R$. Die Abbildung $\pi \colon E \to B$ projiziert jede Gerade E_x auf den Punkt x. Der Raum $E_x=\{p \in E|\pi(p)=x\}$ wird Faser über x genannt. Außerdem ist der Totalraum E die Vereinigung aller Fasern.^[1]

Ein (topologisches) reelles bzw. komplexes Vektorbündel vom Rang n ist ein Tripel (E,B,π), bestehend aus topologischen Räumen E (Totalraum) und B (Basis) sowie einer stetigen surjektiven Abbildung π: E → B, so dass gilt:

• Für jeden Punkt x von B trägt die Faser E_x := π⁻¹(x) von E über x die Struktur eines reellen bzw. komplexen n-dimensionalen Vektorraums.
• „Lokale Trivialität“: Zu jedem Punkt x von B existiert eine Umgebung U von x und ein Homöomorphismus
  $\psi \colon U \times \R^n \to E|_U := \pi^{-1}(U) \subseteq E,$
  der mit π kompatibel ist, das heißt $\pi \circ \psi = \operatorname{pr}_1$, und für den
  $\psi_y \colon \{ y \} \times \R^n \to E_y$
  für jedes y in U ein Isomorphismus von Vektorräumen ist. Dabei bezeichnet pr₁ die Projektion auf den ersten Faktor. Ein solches ψ heißt eine Trivialisierung.

Ein Vektorbündel (E,B,π) heißt trivial, wenn es eine Trivialisierung mit U = B gibt. $(B \times \R^n,B,\operatorname{pr}_1)$ ist ein triviales Vektorbündel.

Sind E und B differenzierbare Mannigfaltigkeiten, und sind π sowie die Trivialisierungen ψ differenzierbar, so heißt das Vektorbündel differenzierbar.

Für (algebraische) Vektorbündel in der algebraischen Geometrie sind E und B Schemata, E_x ist für alle Punkte x von B ein κ(x)-Vektorraum, und die lokalen Trivialisierungen sind Isomorphismen

$U \times A^n \to E|_U$

Meist ist mit „Vektorbündel“ in der algebraischen Geometrie jedoch eine lokal freie Garbe gemeint (s.u.).

Geradenbündel

Ein Vektorbündel mit Rang 1 wird Geradenbündel (denglisch auch Linienbündel) genannt.

Schnitt

→ Hauptartikel: Schnitt (Faserbündel)

Ist U eine offene Teilmenge von B, so heißt eine Abbildung

$s \colon U \rightarrow E|_U\,,$

für die $\pi \circ s = \operatorname{id}|_U$ gilt, ein Schnitt von E über U. Die Menge Γ(U,E) aller Schnitte von E über U bildet einen Vektorraum.

Beispiele

• Das Tangentialbündel einer differenzierbaren Mannigfaltigkeit ist ein Vektorbündel bestehend aus den Tangentialräumen der Mannigfaltigkeit.
• Entsprechend ist auch das Kotangentialbündel bestehend aus den Kotangentialräumen - also den Dualräumen der Tangentialräume - ein Vektorbündel.
• Der Raum der Differentialformen ist als Bündel der äußeren Algebra auch ein Vektorbündel.
• Das (r,s)-Tensorbündel ist ebenfalls ein Vektorbündel, das die zuvor gelisteten Vektorbündel als Spezialfälle umfasst.

Rahmen

Unter einem Rahmen (auf englisch Frame) versteht man eine Art Basis eines Vektorbündels. Es handelt sich um eine Teilmenge des Vektorbündels, welche an jedem Punkt eine Basis des zugehörigen Vektorraums bildet. Präzise bedeutet dies:

Sei $\pi : E \to B$ ein Vektorbündel mit Rang n und sei $U \subset B$ eine offene Teilmenge des Basisraums. Ein lokaler Rahmen von E über U ist ein geordnetes n-Tupel $(\sigma_1, \ldots, \sigma_n)$. Dabei ist für alle i σ_i ein Schnitt in E über U, so dass $(\sigma_1(p), \ldots, \sigma_n(p))$ eine Vektorraumbasis der Faser E_p für alle $p \in U$ bildet. Falls man U = B wählen kann, so spricht man von einem globalen Rahmen.

Lokalfreie Garben

Es sei (X, O_X) ein lokal geringter Raum, z.B. ein topologischer Raum mit der Garbe der stetigen reell- oder komplexwertigen Funktionen, eine differenzierbare Mannigfaltigkeit mit der Garbe der C^∞-Funktionen oder ein Schema.

Eine lokal freie Garbe ist ein O_X-Modul M, der lokal isomorph zu einem freien O_X-Modul ist, d.h. X kann durch offene Mengen U überdeckt werden, für die M|_U isomorph zu einer direkten Summe von Kopien von O_X|_U ist.

Lokalfreie Garben und Vektorbündel

Die beiden folgenden Konstruktionen liefern im Fall von topologischen Räumen oder differenzierbaren Mannigfaltigkeiten eine Äquivalenz der Kategorien von lokal freien Garben sowie Vektorbündeln auf X (der Einfachheit der Notation halber ist der Fall von reellen Vektorbündeln über einem topologischen Raum beschrieben):

• Einem Vektorbündel wird die Garbe seiner Schnitte zugeordnet.
• Einer lokal freien Garbe M wird die disjunkte Vereinigung E ihrer Fasern M_x/m_xM_x zugeordnet. Wir wählen eine offene Überdeckung (U_i) von X, so dass M auf jedem U_i trivial wird. Eine Trivialisierung definiert n nirgends verschwindende Schnitte von M über U_i, die fasernweise eine Basis bilden. Diese definieren eine Abbildung

U_i × Rⁿ → E,

und wir definieren die Topologie auf E dadurch, dass wir fordern, dass diese Abbildungen Homöomorphismen sind. Sie ist wohldefiniert, da sich diese Abbildungen über dem Schnitt zweier Mengen U_i und U_j nur um einen Homöomorphismus (genauer gesagt einen stetig variierenden Vektorraumautomorphismus von Rⁿ) unterscheiden.

Im Fall der algebraischen Geometrie ist diese Konstruktion etwas einfacher: das Bündel zu einer lokalfreien Garbe E ist

V(E^∨) := Spec S(E^∨)

dabei bezeichnet S die symmetrische Algebra und Spec das Algebrenspektrum.

Weiterführende Begriffe

• Die Untersuchung so genannter stabiler Äquivalenzklassen von Vektorbündeln ist Gegenstand der K-Theorie.
• Auf algebraischen Kurven haben (semi-)stabile Vektorbündel besonders gute Eigenschaften.

Einzelnachweise

1. ↑ J. Baez, J. Muniain: Gauge fields, knots and gravity, world scientific (1994), ISBN 9810220340, S. 200

Literatur

• R. Abraham, J. E. Marsden, T. Ratiu: Manifolds, Tensor Analysis, and Applications. 2. Auflage. Springer, Berlin 1988, ISBN 3-540-96790-7. 
• Allen Hatcher: Vector Bundles & K-Theory. Version 2.1, May 2009, online (PDF; 1,11 MB).
• John M. Lee: Introduction to Smooth Manifolds. 2. Auflage. Springer, New York 2003, ISBN 0-387-95448-1.