Stichprobenverteilung

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Unter Stichprobenverteilung versteht man die Verteilung einer Schätzgröße bzw. einer Teststatistik unter hypothetischer Wiederholung der Stichprobennahme. Die Verteilung der Schätzgröße, die als Stichprobe aus einer Grundgesamtheit entnommen wird - wenn in Bezug gesetzt zur Verteilung dieser Schätzgröße in der Grundgesamtheit -, dient der Gewinnung von Aussagen über die Ermittlung dieser Schätzgrößen in der Grundgesamtheit aufgrund von Stichproben aus der Grundgesamtheit. Die Fragestellung lautet also: wie kann man von Stichproben auf die Grundgesamtheit zurück schließen. Die Beantwortung dieser Frage zur Genauigkeit/Zuverlässigkeit des Rückschlusses von einer Stichprobe auf die Grundgesamtheit geht über die Stichprobenverteilung und wird über Konfidenzintervalle bzw. p-Werte bemaßt.

Man spricht statt von Stichprobenverteilung auch einfach von der Verteilung einer Statistik.

Mit Formeln ausgedrückt: für einen bestimmten Datensatz (Stichprobe) X₁ erhält man eine Schätzung 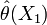$\hat\theta(X_1)$ für die Größe θ. Wenn das Experiment wiederholt wird, ergibt sich i.d.R. ein anderer Datensatz X₂, und damit ein anderes 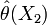$\hat\theta(X_2)$ (man beachte dass 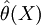$\hat\theta(X)$ selbst eine Zufallsgröße ist, da X eine Zufallsgröße ist). Die Verteilung aller solcher 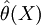$\hat\theta(X)$ für alle möglichen X ist die Stichprobenverteilung.

Die Stichprobenverteilung kann nur in einigen wenigen Fällen -die aber dafür um so wichtiger sind- analytisch bestimmt werden. Die beiden wichtigsten Fälle sind:

• Die Verteilung einer z-Statistik (Mittelwert oder Mittelwertsdifferenz) ist normalverteilt, wenn X normalverteilt ist.
• Die Verteilung der t-Statistik (Mittelwertsdifferenz geteilt durch geschätzte Standardabweichung) folgt einer Studentsche t-Verteilung, wenn X normalverteilt ist.

Wenn der Datensatz X ausreichend groß ist, kann die Stichprobenverteilung für jede beliebige Schätzgröße nichtparametrisch mit Hilfe des Bootstrapping (Statistik) Verfahrens bestimmt werden, ohne dass die Verteilung von X bekannt sein muss.

Die Stichprobenverteilung ist ein frequentistisches Konzept. Das Bayesianische Pendant ist die A-posteriori-Verteilung.