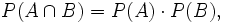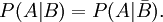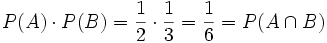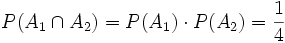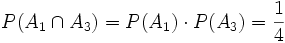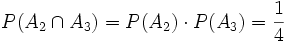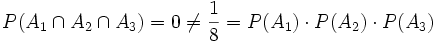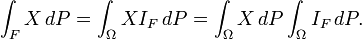- Stochastische Abhängigkeit
-
Unter Stochastischer Unabhängigkeit versteht man in stochastischer, d. h. wahrscheinlichkeitstheoretischer Hinsicht die Vorstellung, dass Ereignisse sich quantitativ, also in Bezug auf ihre Eintrittswahrscheinlichkeit, nicht beeinflussen.
Zum Beispiel geht man davon aus, dass zwei Würfe einer Münze voneinander unabhängig sind, wenn das Ergebnis des zweiten Wurfs nicht vom Ergebnis des ersten Wurfs abhängt. Als Beispiel für zwei voneinander abhängige Ereignisse kann man die Regenwahrscheinlichkeit an zwei aufeinander folgenden Tagen ansehen.
Insbesondere Ereignisse, die mit positiver Wahrscheinlichkeit eintreten und sich gegenseitig ausschließen oder bedingen, sind voneinander abhängig. Dass Ereignisse sich gegenseitig ausschließen, wird häufig mit deren Unabhängigkeit verwechselt.
Inhaltsverzeichnis
Stochastische Unabhängigkeit zweier Ereignisse
Definition
Es sei (Ω,Σ,P) ein Wahrscheinlichkeitsraum und
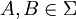 seien zufällige Ereignisse, also messbare Teilmengen der Ergebnismenge Ω.
seien zufällige Ereignisse, also messbare Teilmengen der Ergebnismenge Ω.Dann heißen A und B stochastisch unabhängig, wenn
das heißt, wenn die Wahrscheinlichkeit, dass beide Ereignisse gleichzeitig eintreten, gleich dem Produkt ihrer Einzelwahrscheinlichkeiten ist.
Wenn eines der Ereignisse (z. B. B) die Wahrscheinlichkeit 0 hat, dann gilt auch
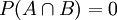 und obige Definitionsgleichung ist erfüllt, ebenso wenn B die Wahrscheinlichkeit 1 hat, dann ist
und obige Definitionsgleichung ist erfüllt, ebenso wenn B die Wahrscheinlichkeit 1 hat, dann ist 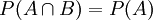 . Deshalb erhält man die trivialen Aussagen, dass jedes Ereignis A sowohl von jedem fast unmöglichen als auch von jedem fast sicheren Ereignis unabhängig ist.
. Deshalb erhält man die trivialen Aussagen, dass jedes Ereignis A sowohl von jedem fast unmöglichen als auch von jedem fast sicheren Ereignis unabhängig ist.Lässt man diese Trivialfälle außer Acht, dann erhält man unter Verwendung des wichtigen Begriffes der bedingten Wahrscheinlichkeit die folgenden äquivalenten Definitionen:
Zwei Ereignisse A und B mit P(A), P(B) > 0 sind genau dann unabhängig, wenn
- P(A|B) = P(A)
oder
Beispiel
Betrachtet wird ein Wurf mit einem „idealen“ Würfel. Die Grundmenge Ω des Wahrscheinlichkeitsraumes sei also Ω = {ω1,...,ω6}, wobei ωi für das Elementarergebnis „die Zahl i wird gewürfelt“ steht. Die Sigma-Algebra Σ sei die Potenzmenge von Ω und das Wahrscheinlichkeitsmaß P ist definiert durch P({ωi}) = 1 / 6 für alle
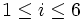 .Es werden nun zwei Ereignisse A und B definiert, wobei A = { es wird eine gerade Zahl gewürfelt } = {ω2,ω4,ω6} und B = { es wird eine durch drei teilbare Zahl gewürfelt } = {ω3,ω6} bedeuten sollen. Nach Definition des Wahrscheinlichkeitsmaßes ist also P ( A ) = 3 / 6 = 1 / 2 und P ( B ) = 2 / 6 = 1 / 3. Für den Durchschnitt von A und B (das heißt es wird eine sowohl durch 2 als auch durch 3 teilbare Zahl gewürfelt), erhält man
.Es werden nun zwei Ereignisse A und B definiert, wobei A = { es wird eine gerade Zahl gewürfelt } = {ω2,ω4,ω6} und B = { es wird eine durch drei teilbare Zahl gewürfelt } = {ω3,ω6} bedeuten sollen. Nach Definition des Wahrscheinlichkeitsmaßes ist also P ( A ) = 3 / 6 = 1 / 2 und P ( B ) = 2 / 6 = 1 / 3. Für den Durchschnitt von A und B (das heißt es wird eine sowohl durch 2 als auch durch 3 teilbare Zahl gewürfelt), erhält man 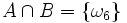 und damit
und damit 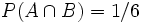 . Wegen
. Wegensind also die Ereignisse { es wird eine gerade Zahl gewürfelt } und { es wird eine durch drei teilbare Zahl gewürfelt } unabhängig.
Stochastische Unabhängigkeit mehrerer Ereignisse
Definition
Sei (Ω,Σ,P) ein Wahrscheinlichkeitsraum, I eine nichtleere Indexmenge und
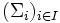 mit
mit 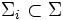 für alle
für alle 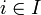 eine Menge nichtleerer Mengensysteme, so heißen
eine Menge nichtleerer Mengensysteme, so heißen 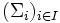 stochastisch unabhängig, wenn für jede endliche Teilmenge,
stochastisch unabhängig, wenn für jede endliche Teilmenge, 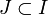 und alle Wahlen
und alle Wahlen 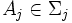 mit
mit 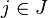 gilt:
gilt: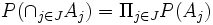 .
.
Eine Menge von Zufallsvariablen heißt stochastisch unabhängig, wenn ihre Urbild-σ-Algebren stochastisch unabhängig bezüglich obiger Definition sind.
Beispiel
Folgendes Beispiel von Bernstein (1928) zeigt die paarweise Unabhängigkeit von drei Ereignissen A1, A2 und A3, die aber nicht gemeinsam (also A1, A2 und A3 gleichzeitig) unabhängig sind.
In einer Schachtel befinden sich 4 Zettel mit folgenden Zahlenkombinationen: 112, 121, 211, 222. Einer der Zettel wird zufällig (je mit Wahrscheinlichkeit 1/4) gezogen. Wir betrachten dann folgende drei Ereignisse:
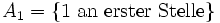 mit
mit 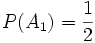
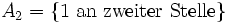 mit
mit 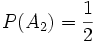
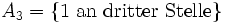 mit
mit 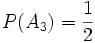
Offensichtlich sind die drei Ereignisse paarweise unabhängig, da gilt
Die drei Ereignisse sind jedoch nicht (gemeinsam) unabhängig, da gilt
Des Weiteren kann aus
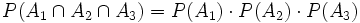 nicht geschlossen werden, dass die drei Ereignisse paarweise unabhängig sind.
nicht geschlossen werden, dass die drei Ereignisse paarweise unabhängig sind.Bemerkungen
Bei methodisch korrektem Vorgehen kann man nicht einfach Unabhängigkeit vermuten, sondern man muss sie anhand obiger Formel überprüfen. Dabei ist meistens die gemeinsame Wahrscheinlichkeit P(A ∩ B) nicht von vornherein gegeben. Bei der praktischen Auswertung erhobener Daten kann man beispielsweise mit einem χ2-Test die Merkmale auf stochastische Unabhängigkeit testen.
Für die Analyse auf Abhängigkeit zweier Zufallsvariablen kann man auch testen, ob der Korrelationskoeffizient Null ist. Wenn die Hypothese abgelehnt wird, geht man davon aus, dass diese Variablen stochastisch abhängig sind. Der Umkehrschluss ist allerdings nicht zulässig, denn es können Abhängigkeitsstrukturen vorliegen, die der Korrelationskoeffizient nicht erfassen kann. Jedoch sind beispielsweise unkorrelierte, gemeinsam normalverteilte Zufallsvariablen auch stochastisch unabhängig.
Noch etwas weiter wird der Begriff der stochastischen Unabhängigkeit von Zufallsvariablen von Filtrationen gefasst: X heißt von
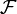 unabhängig, wenn für
unabhängig, wenn für 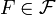 gilt:
gilt:Siehe auch
Wikimedia Foundation.