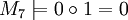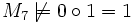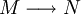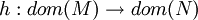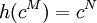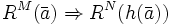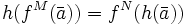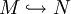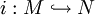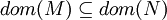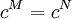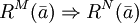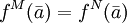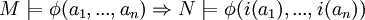- Struktur (Modelltheorie)
-
Zu jeder Elementaren Sprache L können zugehörige Strukturen definiert werden. Eine L-Struktur M besteht aus einem Grundbereich, den Elementen von M, ausgezeichneten Elementen, den Konstanten von M, und aus Beziehungen zwischen der Elementen, die durch Relationen und Funktionen über dem Grundbereich beschrieben werden. Die Konstanten, Relationen und Funktionen der Struktur sind die Interpretationen der Symbole die zu der Signatur der Sprache gehören. Mit einer L-Struktur M kann der Wert
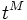 bzw.
bzw. 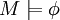 von beliebigen Termen
von beliebigen Termen 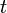 und Formeln
und Formeln 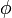 der Elementaren Sprache gefolgert werden. Die Menge der Aussagen, die aus einer Struktur folgt, wird als Theorie von M Th(M) bezeichnet. Umgekehrt können zu einer Aussagenmenge Σ aus L die Klasse Mod(Σ) der L-Strukturen, die sogenannten Modelle von Σ, angeben werden, aus denen Σ gefolgert werden kann. Im Beweis des Gödelschen 1. Vollständigkeitssatzes wird auch beschrieben, wie zu jeder konsistenen Mengen von Aussagen ein Modell definiert werden kann.
der Elementaren Sprache gefolgert werden. Die Menge der Aussagen, die aus einer Struktur folgt, wird als Theorie von M Th(M) bezeichnet. Umgekehrt können zu einer Aussagenmenge Σ aus L die Klasse Mod(Σ) der L-Strukturen, die sogenannten Modelle von Σ, angeben werden, aus denen Σ gefolgert werden kann. Im Beweis des Gödelschen 1. Vollständigkeitssatzes wird auch beschrieben, wie zu jeder konsistenen Mengen von Aussagen ein Modell definiert werden kann.Inhaltsverzeichnis
Definition von L-Strukturen
Jeder Elementaren Sprache L kann eine Klasse von L-Strukturen zugeordnet werden. Zur Definition von L-Strukturen wird von der Sprache L nur die Signatur
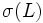 der Sprache benötigt.
der Sprache benötigt.Signatur
Sei eine Signatur
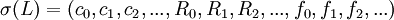 aus Konstanten-, Relations- und Funktionssymbolen gegeben.
aus Konstanten-, Relations- und Funktionssymbolen gegeben.- Beispiele
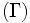 , zweistellige Relation
, zweistellige Relation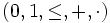 , wobei die Relationen und Funktionen zweistellig
, wobei die Relationen und Funktionen zweistellig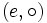
Interpretation einer Signatur in einer Struktur
Eine Struktur zu einer Signatur besteht aus
- Grundbereich:
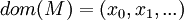 den Elementen der Struktur (auch Universum von M oder Domain von M).
den Elementen der Struktur (auch Universum von M oder Domain von M). - Den Interpretationen der Symbole der Signatur:
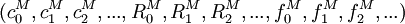
- Jedem Konstantensymbol
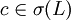 wird ein Element zugeordnet, also
wird ein Element zugeordnet, also 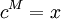 für ein
für ein 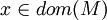 .
. - Jedem n-stelligem Relationssymbol
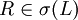 wird eine n-stellige Relation über
wird eine n-stellige Relation über 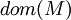 zugeordnet. Also
zugeordnet. Also 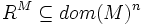 .
. - Jedem n-stelligen Funktionssymbol
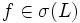 wird eine n-stellige Funktion über
wird eine n-stellige Funktion über 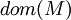 zugeordnet. Also
zugeordnet. Also 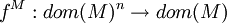 .
.
- Jedem Konstantensymbol
Beispiele
Signatur 1
Zu der Signatur
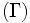 , wobei die Relation zweistellig, können wir folgende L-Strukturen definieren, die allesamt gerichtete Graphen sind:
, wobei die Relation zweistellig, können wir folgende L-Strukturen definieren, die allesamt gerichtete Graphen sind:1.1 Die Struktur M1:
- dom(M1) = {a,b,c}
- Die Interpretation von Γ in M1:
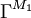 (Zweistellig)
(Zweistellig)
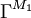
1 2 3 1 f w w 2 w f w 3 w w f 1.2 Die Struktur M2:
- dom(M2) = {1,2,3,4,5,...}
- Die Interpretation von Γ in M2:
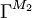 (Zweistellig)
(Zweistellig)
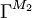
1 2 3 4 ... 1 f w f f ... 2 f f w f ... 3 f f f w ... ... 1.3 Die Struktur M3:
- dom(M3) = {0,1}
- Die Interpretation von Γ in M3:
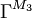 (Zweistellig)
(Zweistellig)
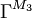
0 1 0 w f 1 f w Signatur 2
Zu der Signatur
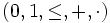 , wobei die Relationen und Funktionen zweistellig, können folgende L-Strukturen definiert werden:
, wobei die Relationen und Funktionen zweistellig, können folgende L-Strukturen definiert werden:2.1 Die Struktur der Natürliche Zahlen M4:
- dom(M4) = (0,1,2,3,...) (Alternativ kann bei 1 begonnen werden)
- Die Symbole werden im üblichen Sinne Interpretiert.
2.2 Die Struktur der Ganzen Zahlen M5:
- dom(M5) = (..., − 3, − 2, − 1,0,1,2,3,...)
- Die Symbole werden im üblichen Sinne Interpretiert.
2.3 Die Struktur der Rationalen Zahlen M6:
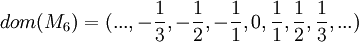
- Die Symbole werden im üblichen Sinne Interpretiert.
Signatur 3
Zur Signatur
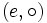 gibt es folgende Beispiele:
gibt es folgende Beispiele:3.1.
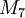 sei die Additive Gruppe von
sei die Additive Gruppe von 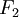 :
: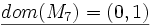
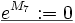
- Die Interpretation der zweistelligen Verknüpfung
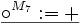

0 1 0 0 1 1 1 0 3.2.
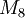 sei die Multiplikative Gruppe von
sei die Multiplikative Gruppe von 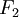 :
: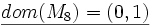
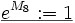
- Die Interpretation der zweistelligen Verknüpfung
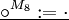

0 1 0 0 0 1 0 1 3.3.
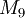 soll das Multiplizieren von Vorzeichen modellieren (minus mal minus ist plus):
soll das Multiplizieren von Vorzeichen modellieren (minus mal minus ist plus):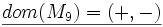
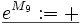
- Die Interpretation der zweistelligen Verknüpfung
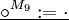

+ − + + − − − + Gültigkeit in L-Strukturen
Für jede L-Struktur kann der Wert eines Termes und der Wert oder die Gültigkeit einer Formel aus der Elementaren Sprache L bestimmt werden.
Wert von Termen in verschiedenen Strukturen
Struktur 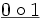
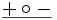
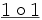
M7 1 nicht def. 0 M8 1 nicht def. 1 M9 nicht def. − nicht def. Wir schreiben allgemein für eine beliebige L-Struktur M und einen Term t aus der zugehörigen elementaren Sprache tM = a wenn t in M den Wert a hat.
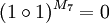 , hier bedeutet
, hier bedeutet  plus im Körper mit zwei Elementen
plus im Körper mit zwei Elementen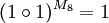 , hier bedeutet
, hier bedeutet  mal im Körper mit zwei Elementen
mal im Körper mit zwei Elementen
Beispiel: Gültigkeit von einer Atomformel, die mit einem Relationssymbol gebildet wurde
Wenn wir ein Formel φ(x1,...,xn) ist ein passendes Tupel (a1,...,an) von Elementen aus M eine Belegung von x1,...,xn. Im folgenden Beispiele für Belegungen von x1,x2 in
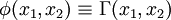 und ihre Gültigkeit in verschiedenen Strukturen.
und ihre Gültigkeit in verschiedenen Strukturen.Struktur 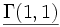
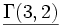
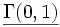
M1 falsch wahr nicht def. M2 falsch falsch nicht def. M3 wahr nicht def. falsch Wenn in einer L Struktur M ein Formel φ(x1,...,xn) mit einer Belegung (a1,...,an) gilt, schreiben wir
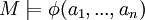 und sagen In M ist gültig ...
und sagen In M ist gültig ...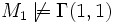 gesprochen In M1 gilt nicht ...
gesprochen In M1 gilt nicht ...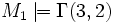
Beispiel: Gültigkeit von einer Atomformel, die mit einem Funktionssymbol gebildet wurde
Nun Beispiele für die Belegung von
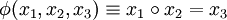 in verschiedenen Strukturen.
in verschiedenen Strukturen.Struktur 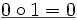
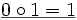
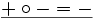
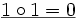
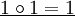
M7 wahr falsch nicht def. wahr falsch M8 wahr falsch nicht def. falsch wahr M9 nicht def. nicht def. wahr nicht def. nicht def. Abbildungen zwischen L-Strukturen
L-Strukturen können nun mehr oder wenig ähnlich sein. Die Ähnlichkeit wird durch besondere Abbildungen zwischen den Grundbereichen ausgedrückt. Die Besonderheit drückt sich in Eigenschaften aus, die für mit den Strukturen verbundenen Ausdrücken, wie die Interpretation der Symbole der Signatur, den Wert von Termen in der Struktur oder die Gültigkeit von Formeln gelten.
- Seien nun M und N zwei Strukturen zur selben Sprache L.
- c, R und f seien beliebige Konstanten-, Relations- und Funktionssymbole aus der Signatur.
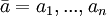 bzw. a seien beliebige Elemente aus dom(M).
bzw. a seien beliebige Elemente aus dom(M).- φ sei eine beliebige Aussage aus L (d.h. eine Formel ohne freie Variablen.
- φ(x1,...,xn) sei eine beliebige Formel aus L mit freien Variablen aus x1,...,xn.
Beziehung der Strukturen Abbildung Eigenschaft der Abbildung 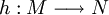
- L-Homomorphismus h
- i ist L-Homomorphismus
- i ist injektiv
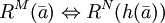
- M und N sind isomorph
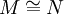
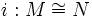
- L-Isomorphismus i
- i ist bijektive L-Einbettung
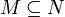
- N ist L-Erweiterung von M
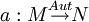
- Automorphismus a
- dom(M) = dom(N)
- a ist Isomorphismus
- N und M sind elementar äquivalent
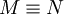
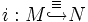
- Elementare Einbettung i
- N ist elementare Erweiterung von M
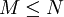
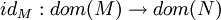 ist elem.Einbettung
ist elem.Einbettung
Ausblick
Abgeleitete Strukturen
Aus vorhandenen Strukturen können neue Strukturen definiert werden
- Quotientenstrukturen
- Unterstrukturen, Oberstrukturen
- Direkte (Kartesische) Produkte
- Redukte, Expansionen
Verallgemeinerungen
Zu den L-Strukturen existieren Verallgemeinerungen
- Many-sorted Structures
- Many-valued Structures
Siehe auch
Quellen
- David Marker, Model Theory: An Introduction.
- Heinz-Dieter Ebbinghaus, Jörg Flum und Wolfgang Thomas, Einführung in die mathematische Logik.
- Beispiele
Wikimedia Foundation.