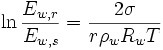Thomson-Gleichung

Bei Bildung von Flüssigkeitspartikel an Kondensationskernen tritt der Krümmungseffekt auf. Es zeigt sich dabei, dass über den gekrümmten Oberflächen der entstehenden Flüssigkeitstropfen ein höherer Sättigungsdampfdruck auftritt, als im Vergleich zu einer ebenen Wasseroberfläche. Dies liegt an der höheren Oberflächenspannung der Tropfen (siehe Young-Laplace-Gleichung), gegen die Arbeit verrichtet werden muss. Den genauen Zusammenhang spiegelt die nach Lord Kelvin benannte Kelvin-Gleichung (auch Thomson-Gleichung) wider:

$\ln \frac{E_{w, r}}{E_{w, s}} = \frac{2\sigma}{r \rho_w R_w T}$

Die einzelnen Formelzeichen stehen für folgende Größen:

• E_r – Sättigungsdampfdruck über dem Tropfen (Messung)
• E_s – Sättigungsdampfdruck über einer ebenen Flüssigkeitsoberfläche (Magnus-Formel)
• R_w – Gaskonstante (z. B. für Wasserdampf = 461,6 J/(kg·K))
• σ – Oberflächenspannung (temperaturabhängig)
• ρ_w – Dichte des Gases
• r – Tropfenradius

Die Gleichungen zeigen im Fall von Wasser für einen Tropfen von 1 µm einen um 12 % erhöhten Sättigungsdampfdruck, welcher jedoch bei 10 µm nur noch um 1,2 % und bei 0,1 mm nur noch um 0,12 % vom planaren Vergleichsdruck abweicht. Je kleiner also die Tropfen sind, desto einfacher verdampfen sie wieder. Dies hat vor allem bei der Tropfenbildung in der Atmosphäre durch Nukleation bzw. Kondensation zur Folge, dass eine Dampfdruckerhöhung bzw. Übersättigung notwendig wird, um die Tropfen bei Reduzierung des Tropfenradius in einem Gleichgewicht zu halten. Genau andersherum verhält sich der Dampfdruck bei Konkaven Oberflächen, zum Beispiel in Kapillaren. Hier wird der Dampfdruck mit abnehmendem Kapillarendurchmesser vermindert. Dies erklärt zum Beispiel die hygroskopische Wirkung von feinporigen, benetzbaren Materialien.

Datei:Dampfdruckerhöhung durch Oberflächenkrümmung.jpg

Kritische Radien

Sättigungsverhältnis S	kritischer Radius in nm	Molekülzahl n
1	∞ (ebene Fläche)	∞
1,01	120	2,5·108
1,1	12,6	2,8·105
1,5	2,96	3650
2	1,73	730
3	1,09	183
4	0,87	90
5	0,75	60
10	0,52	20

In der nebenstehenden Tabelle sind die kritischen Radien und Molekülzahlen von reinen Wassertröpfchen berechnet. Für die spontane Bildung eines Tröpfchens aus nur zwanzig Molekülen müsste die Luft 1000 % übersättigt sein, was in der Natur kaum vorkommt. Andernfalls würde das Tröpfchen sofort wieder verdunsten. Das belegt die Notwendigkeit von Kondensationskernen.

Literatur

• W. T. Thomson, Phil. Mag. 42, 448 (1871)
• Zmarsly E., Kuttler W., Pethe H.: Meteorologisch-klimatologisches Grundwissen. Eine Einführung mit Übungen, Aufgaben und Lösungen. Ulmer Verlag, Stuttgart 2002; ISBN 3-8252-2281-0
• S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, 2nd edition, Academic Press, New York, (1982) p.121
• Adamson and Gast, Physical Chemistry of Surfaces, 6th edition, (1997) p.54