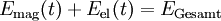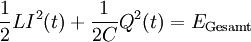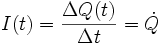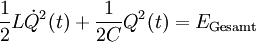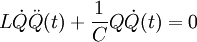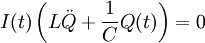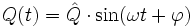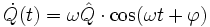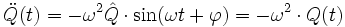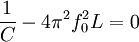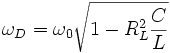Thomson-Formel

Mit der Thomsonschen Schwingungsgleichung lässt sich die Resonanzfrequenz f₀ eines Schwingkreises mit der Kapazität C und der Induktivität L berechnen. Sie wurde 1853 von dem britischen Physiker William Thomson, dem späteren Lord Kelvin, entdeckt.

$f_0 = \frac{1}{2\pi\sqrt{LC}}$

Oder umgeformt für die Schwingungszeit:

$T = 2\pi\sqrt{LC}$,

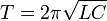wobei π die Kreiszahl ist.

Herleitung

Im Resonanzfall ist der Resonanzwiderstand so groß wie der Serienwiderstand. Der kapazitive Widerstand des Kondensators und induktiver Widerstand der Spule innerhalb des Schwingkreises kompensieren sich auf null.

X_L − X_C = 0

$\omega_0 L = \frac{1}{\omega_0 C}$

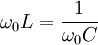
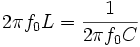$2\pi f_0 L = \frac{1}{2\pi f_0 C}$ , da gilt ω = 2πf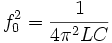

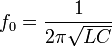$f_0^2 = {\frac{1}{4\pi^2LC}}$

$f_0 = \frac{1}{2\pi\sqrt{LC}}$ , üblich ist auch die Form: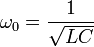 $\omega_0 = \frac{1}{\sqrt{LC}}$

Herleitung nach dem Energieerhaltungssatz

Betrachten wir den elektrischen Schwingkreis als ein geschlossenes System, so ist die Summe aller Energieformen in diesem System zu jeder Zeit t konstant.

$\!\,E_\mathrm{mag}(t)+E_{\rm el}(t) = E_{\rm Gesamt}$

E_mag: magnetische Feldenergie der Spule

E_el: elektrische Feldenergie des Kondensators

E_Gesamt: Gesamtenergie des Systems (konstant)

Setzt man die entsprechenden Formeln ein, so kommt man auf folgende Differentialgleichung:

$\frac{1}{2}LI^2(t) + \frac{1}{2C}Q^2(t) = E_\mathrm{Gesamt}$

Aus

$I(t) = \frac{\Delta Q(t)}{\Delta t} = \dot Q$

folgt:

$\frac{1}{2}L\dot Q^2(t) + \frac{1}{2C}Q^2(t) = E_\mathrm{Gesamt}$

Nun leitet man diese Gleichung nach der Zeit ab und erhält:

$L\dot Q \ddot Q(t)+\frac{1}{C}Q \dot Q(t) = 0$

$I(t)\left(L \ddot Q + \frac{1}{C}Q(t)\right) = 0$

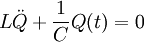$L \ddot Q + \frac{1}{C}Q(t) = 0$, da im Schwingkreis gilt: $I(t) \ne 0$.

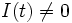Um diese Gleichung zu lösen, müssen wir einen Zusammenhang zwischen Q(t) und 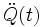$\ddot Q(t)$ herstellen. Dazu verwenden wir eine Sinusfunktion als Lösungsansatz, da sie sich auf Grund ihrer Periodizität gut zur Beschreibung einer Schwingung eignet.

$Q(t) = \hat Q \cdot \sin(\omega t + \varphi)$

$\dot Q(t) = \omega \hat Q \cdot \cos(\omega t + \varphi)$

$\ddot Q(t) = -\omega^2 \hat Q \cdot \sin(\omega t + \varphi) = -\omega^2 \cdot Q(t)$

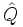$\hat Q$: maximale Ladung (Amplitude)

ω: Winkelgeschwindigkeit

$\varphi$: Phasenverschiebung

Durch Einsetzen ergibt sich:

$\frac{1}{C}Q(t)-\omega^2 L Q(t) = 0$

$Q(t)\left(\frac{1}{C} - \omega^2 L\right) = 0$

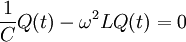
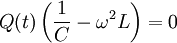
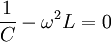$\frac{1}{C} - \omega^2 L = 0$, da im Schwingkreis gilt: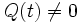 $Q(t) \ne 0$

Daraus folgt mit ω = 2πf:

$\frac{1}{C} - 4 \pi^2 f_0^2 L = 0$

$f_0^2 = {\frac{1}{4\pi^2LC}}$

$f_0 = \frac{1}{2\pi\sqrt{LC}}$

Die Thomsonsche Schwingungsgleichung gilt allerdings nur für reine Serienschwingkreise und reine Parallelschwingkreise. Bei komplexeren Topologien gilt es, die Frequenz für die Erfüllung der folgenden Bedingung selbst herzuleiten:

X_L = X_C

Des Weiteren muss bei der Anwendung der Thomsonschen Schwingungsgleichung darauf geachtet werden, dass sich das jeweilige System im Schwingfall befindet - die Dämpfung durch den ohmschen Widerstand also nicht zu groß ist. Bei nicht zu grosser Dämpfung kann die veränderte Resonanzfrequenz, mit dem Verlustwiderstand R_L von L, berechnet werden:

$\omega_D = \omega_0{\sqrt{1-R_L^2 \frac{C}L}}$

Siehe auch

Andere Herleitung der Formel durch den Energiesatz