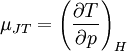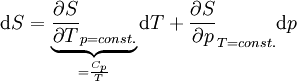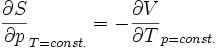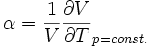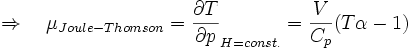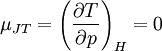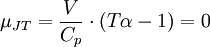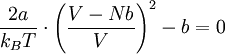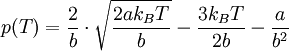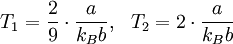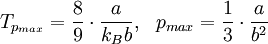Joule-Thomson-Prozess

Nebel kondensierter Luftfeuchtigkeit durch entspanntes Flüssiggas

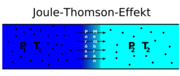
Der Joule-Thomson-Effekt, nicht zu verwechseln mit dem Thomson-Effekt, tritt auf, wenn ein reales Gas oder Gasgemisch durch Drosselung (=Druckänderung) eine Temperaturänderung erfährt. Diese Erscheinung spielt eine wichtige Rolle in der Thermodynamik von Gasen und ist vor allem für die Technik von Bedeutung. Eine wichtige großtechnische Anwendung ist die Gasverflüssigung im Linde-Verfahren.

Schematische Darstellung des Joule-Thomson-Effektes

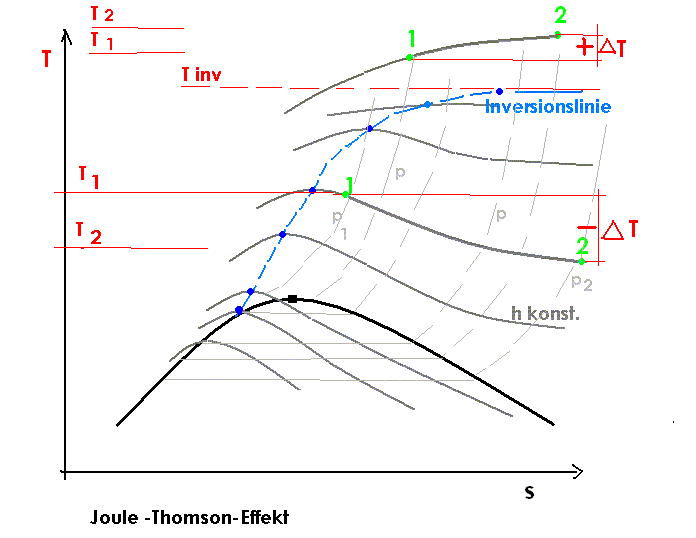
Drosselt man ein Gas, etwa indem man in einer Rohrleitung eine Blende oder anderes Hindernis einbaut (siehe Grafik), expandiert es. Das heißt, das vom Gas eingenommene Volumen hinter dem Hindernis nimmt zu. Dabei erhöht sich der mittlere Teilchenabstand, wodurch sich die Temperatur des Gases ändert.

Geschichtliches

Der Joule-Thomson-Effekt wurde nach James Prescott Joule und Sir William Thomson (dem späteren Lord Kelvin) benannt, die dieses Phänomen im Jahre 1852 beschrieben.

Thermodynamik

Joule-Thomson-Koeffizient

Die Stärke und Richtung der Temperaturänderung wird durch den Joule-Thomson-Koeffizient μ beschrieben:

$\mu_{JT} = \left( \frac{ \partial T }{ \partial p }\right)_H$

Er stellt die partielle Ableitung der Temperatur T nach dem Druck p bei konstanter Enthalpie H dar. Der Vorgang ist also isenthalp, was durch den Index H angedeutet wird.

Die Ursache des Joule-Thomson-Effekts liegt in der Wechselwirkung der Gasteilchen. Ziehen sich die Teilchen an, muss bei der Vergrößerung des Teilchenabstandes Arbeit gegen diese Anziehung geleistet werden. Die Energie dazu kommt aus der kinetischen Energie der Gasteilchen, das Gas kühlt ab. Stoßen sich die Teilchen hingegen ab, so ist im gepressten Zustand mehr Energie vorhanden. Wenn die Teilchen sich voneinander weg bewegen können (Expansion), wird diese Energie frei. Der kinetische Anteil vergrößert sich also und die Temperatur des Gases steigt. Dies nehmen wir als Wärme wahr.

Ob sich die Teilchen eines Gases anziehen oder abstoßen, hängt von der Temperatur des Gases ab. In der Regel existieren für jedes Gas zwei Temperaturen, bei denen sich das Verhalten ändert. Diese Temperaturen nennt man die obere und die untere Inversionstemperatur. Bei Luft liegt die obere Inversionstemperatur bei +450°C. Oberhalb dieser Temperatur führt der Joule-Thomson-Effekt zu Erwärmung. Unterhalb tritt Abkühlung auf. Will man im Linde-Verfahren Wasserstoff oder Helium abkühlen, muss man die Gase vorkühlen, da ihre Inversionstemperaturen bei -80°C bzw. -239°C liegen.

Im Modell des idealen Gases werden keine Wechselwirkungen zwischen den Teilchen berücksichtigt. Ideale Gase weisen daher keinen Joule-Thomson-Effekt auf.

Herleitung des Joule-Thomson-Koeffizienten

Thermodynamisch bleibt die Enthalpie H erhalten. Dies sieht man wie folgt: Zunächst ist das Gas in einem Volumen V₁ eingeschlossen, es herrscht der Druck p₁ und die Temperatur T₁. Nun wird das Gas in das Volumen V₂ gedrückt. Damit das Gas keine kinetische Energie aufbauen kann, geschieht die Überführung von V₁ nach V₂ durch eine Drossel (eine andere Funktion hat die Drossel nicht). Das Gas im Volumen V₁ strömt aufgrund des Drucks p₁ "von alleine" durch die Drossel. Die Energie (Volumenarbeit), die im Druck steckt, wird frei p₁V₁. Andererseits wird im Volumen V₂ ein Druck aufgebaut. Die hierfür benötigte Arbeit p₂V₂ muss vom Gas aufgebracht werden. Nun wird die Energieerhaltung benutzt: Die innere Energie E des Gases ändert sich aufgrund der erbrachten Arbeit

E₁ + p₁V₁ = E₂ + p₂V₂.

Dies ist gerade die Enthalpieerhaltung.

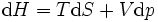$\mathrm dH = T \mathrm dS + V \mathrm dp \!$ mit $H = U + pV \!$

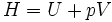
Totales Differential der Entropie S(T,p):

$\mathrm dS=\underbrace{\frac{\partial S}{\partial T}_{p=const.}}_{=\frac{C_p}{T}} \mathrm dT + \frac{\partial S}{\partial p}_{T=const.} \mathrm dp$

Maxwellrelation der freien Enthalpie G:

$\frac{\partial S}{\partial p}_{T=const.} = -\frac{\partial V}{\partial T}_{p=const.}$

Thermischer Ausdehnungskoeffizient:

$\alpha = \frac{1}{V}\frac{\partial V}{\partial T}_{p=const.}$

$\Rightarrow \quad \mu_{Joule-Thomson}=\frac{\partial T}{\partial p}_{H=const.} = \frac{V}{C_p}(T\alpha-1)$

Für ein ideales Gas ist α = 1 / T und somit ist der Joule-Thomson-Effekt nicht vorhanden, seine innere Energie hängt nicht vom Volumen ab. Dies sollte nicht verwundern, da es zwischen den Teilchen des idealen Gases per Definition keine Wechselwirkung gibt. Bei realen Gasen ist der Effekt hingegen auch bei geringen Drücken und hohen Temperaturen, wo sie sich nahezu ideal verhalten, gegeben.

Hierbei stehen die einzelnen Formelzeichen für folgende Größen:

• C_p - Wärmekapazität bei konstantem Druck
• α - Wärmeausdehnungskoeffizient

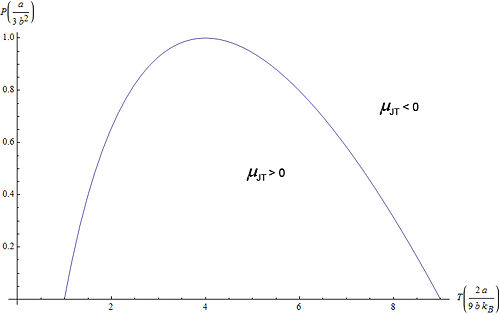
Joule-Thomson-Inversionskurve

Die Kurve im Druck-Temperatur-Diagramm für die

$\mu_{JT} = \left( \frac{ \partial T }{ \partial p }\right)_H = 0$

gilt wird als Joule-Thomson-Inversionskurve bezeichnet. Im von der Kurve eingeschlossenen Bereich gilt μ_JT > 0, außerhalb gilt μ_JT < 0.

Joule-Thomson-Inversionskurve für ein Van-der-Waals-Gas

Joule-Thomson-Inversionskurve für ein reales Gas in einem P-T-Diagramm

$\mu_{JT} = \frac{V}{C_p}\cdot(T\alpha-1) = 0$

Nach Einsetzen des Wärmeausdehnungskoeffizienten (α) erhält man folgende Gleichung:

$\frac{2a}{k_BT}\cdot\left(\frac{V-Nb}{V}\right)^2-b=0$

Durch Auflösen dieser Gleichung nach V und Einsetzen in die Van-der-Waals-Gleichung ergibt sich die Joule-Thomson-Inversions-Gleichung p(T):

$p(T)=\frac{2}{b}\cdot \sqrt{\frac{2ak_BT}{b}} - \frac{3k_BT}{2b} - \frac{a}{b^2}$

Für diese Gleichung ergeben sich folgende Nullstellen:

$T_1=\frac{2}{9} \cdot \frac{a}{k_Bb},\,\,\,\, T_2=2\cdot \frac{a}{k_Bb}$

und folgende Extrema:

$T_{p_{max}}=\frac{8}{9}\cdot\frac{a}{k_Bb}, \,\,\,\, p_{max}=\frac{1}{3}\cdot \frac{a}{b^2}$

Technische Aspekte

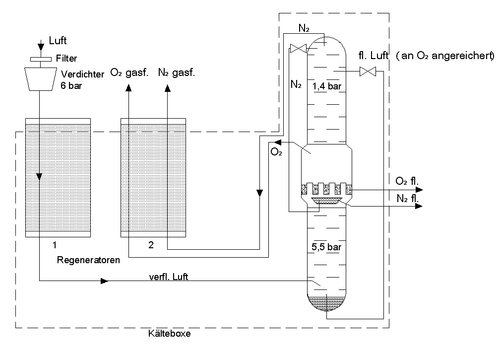Das Linde-Verfahren

Das Linde-Verfahren zur Gasverflüssigung setzt einen positiven Joule-Thomson-Koeffizienten voraus. Nur so kann die Energie des komprimierten Gases abgeführt werden, obwohl die Umgebungstemperatur höher ist als die des Gases. In der Linde-Maschine wird Luft durch ein Drosselventil von etwa 200 bar auf etwa 20 bar entspannt. Dabei kühlt sie sich um etwa 45 Kelvin ab. Die abgekühlte Luft wird nun genutzt, um weitere komprimierte Luft vor der Entspannung abzukühlen (Gegenstrom-Wärmeübertrager). Über mehrere Kompressions- und Entspannungsstufen kann somit das Gas so weit abgekühlt werden, dass es kondensiert und somit flüssig wird.

Da der Joule-Thomson-Koeffizient von der Temperatur abhängt, kann es je nach verwendetem Gas sein, dass selbiges vorgekühlt werden muss, da es sich sonst noch weiter erwärmt, anstatt sich weiter abzukühlen. Beispielsweise muss Helium erst mit anderen Methoden auf ungefähr -228 °C (45 K) abgekühlt werden.

Ein positiver Joule-Thomson-Koeffizient ist neben der Reibung mitverantwortlich dafür, dass Kompressionsanlagen gekühlt werden müssen, beziehungsweise dass komprimierte Gase bei einer höheren Umgebungstemperatur Wärme abgeben können. Dies wird bei der Brüdenkompression eingesetzt.

Anwendungen

• Gasverflüssigung (Linde-Verfahren)
• Eine Folge des Effekts kann die Abkühlung von Erdgas in Pipelines sein. Durch den hohen Massestrom unter Druckabfall kann es unter ungünstigen Bedingungen zu (unerwünschten) Vereisungen der Pipelines kommen. Um dem vorzubeugen, kann es erforderlich sein, bei der Einspeisung bzw. vor der Druckreduzierung in Gas-Druckregelanlagen das Erdgas vorzuwärmen. Beispielsweise wird Erdgas bei 200 – 250 bar in Salz- oder Gesteinskavernen sowie Aquifer-Speichern gelagert. Wird das Gas nun in Pipelines, welche es zum Verbraucher transportieren, eingeleitet, kühlt sich das Gas stark ab, da in den (überregionalen) Pipelines ein Druck von weniger als 100 bar herrscht. Damit kein Kondensat ausfällt und es zu keiner Vereisung in nachgelagerten Anlagenteilen oder im Boden kommt, wird das gespeicherte Gas, bevor es entspannt wird, vorgewärmt. Die Vorwärmung muss so hoch sein, dass nach der Entspannung nicht der Wasserdampftaupunkt bzw. Gastaupunkt unterschritten wird. Der gleiche Effekt tritt in allen nachgelagerten Gasanlagen auf, in denen eine weitere Druckreduzierung erfolgt. Auch in diesen wird das Erdgas vor der Entspannung erwärmt. Bei Differenzdrücken (Druckdifferenz vor und nach der Anlage) von weniger als ca. 12 bar wird der Effekt vernachlässigt und das Erdgas wird nicht vorgewärmt.

Literatur

• Peter W. Atkins: Physikalische Chemie. Wiley-VCH, Weinheim 2001, ISBN 3-527-30236-0.
• Refah Ayber: Thomson-Joule-Effekt von Methan-Wasserstoff- und Äthylen-Wasserstoff-Gemischen (VDI-Forschungsheft; Bd. 511). VDI-Verlag, Düsseldorf 1965.
• Lew Dawidowitsch Landau und Jewgeni Michailowitsch Lifschitz: Lehrbuch der Theoretischen Physik. Akademie-Verlag, Berlin
  • 5. Statistische Physik. 1987, ISBN 3-05-500069-2.