- Tic Tac Toe
-
Tic Tac Toe (auch: Drei gewinnt, XXO, Kreis und Kreuz, Dodelschach oder engl. Noughts and Crosses) ist ein klassisches, einfaches Zweipersonen-Strategiespiel, dessen Geschichte sich bis ins 12. Jahrhundert v. Chr. zurückverfolgen lässt.
Inhaltsverzeichnis
Spielverlauf
Auf einem 3×3 Felder großen Spielfeld machen die beiden Spieler abwechselnd ihre Zeichen (ein Spieler Kreuze, der andere Kreise). Der Spieler, der als erstes drei seiner Zeichen in eine Reihe, Spalte oder eine der beiden Hauptdiagonalen setzen kann, gewinnt. Wenn allerdings beide Spieler optimal spielen, kann keiner gewinnen, und es kommt zu einem Unentschieden.
Beispielpartien
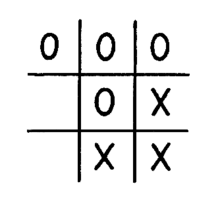
Erster Spieler (X) gewinnt, weil Spieler Zwei (O) in der ersten Runde einen Fehler macht:

Erster Spieler (X) gewinnt, weil Spieler Zwei (O) in der ersten Runde einen Fehler macht:
Erster Spieler (X) verliert, weil er in der zweiten Runde einen Fehler macht:
Kein Spieler gewinnt, da beide fehlerfrei spielen:
Strategie und Taktik
Für Tic Tac Toe gibt es 255.168 verschiedene Spielverläufe, von denen 131.184 mit einem Sieg des ersten Spielers enden, 77.904 mit einem Sieg des zweiten Spielers und 46.080 mit einem Unentschieden. (Bei diesen Zahlenangaben wird die erste Konfiguration mit drei X oder drei O in einer Reihe, Spalte oder Diagonale oder ein vollständig ausgefülltes Spielfeld, aber nicht bereits die Situation, ab der der Ausgang feststeht, als Ende des Spiels betrachtet.)
Viele Spielverläufe sind gleich in dem Sinne, dass sie sich durch Drehungen oder Spiegelungen des Spielfelds ineinander überführen lassen. Gleiche Verläufe zusammengefasst, vermindert sich die Zahl der verschiedenen Spielverläufe auf ein Achtel: insgesamt 31.896, wobei 16.398 vom ersten und 9.738 vom zweiten Spieler gewonnen werden und 5.760 unentschieden ausgehen. (Aus jedem Spielverlauf erhält man durch Rotationen und Spiegelungen sieben weitere Spielverläufe, denn da am Ende immer mindestens fünf Felder belegt sind, ist kein Spielverlauf symmetrisch bezüglich einer Rotation oder Spiegelung.)
Es gibt 5.478 verschiedene Spielsituationen, ohne Rotation oder Spiegelung 765. Im Vergleich zu Spielen wie Go, Dame oder Schach ist die Anzahl der Spielverläufe und Spielsituationen verschwindend gering. Wegen dieser geringen Komplexität lässt sich leicht zeigen, dass beide Spieler ein Unentschieden erzwingen können.
Der erste Spieler kann nicht bereits im ersten Zug verlieren. Der zweite Spieler hält nur in 24 von den 72 Möglichkeiten für die beiden ersten Züge ein Unentschieden.
Erster Spieler (X) beginnt, zweiter Spieler (O) hält ein Unentschieden (gespiegelte und rotierte Möglichkeiten sind nicht dargestellt):

Es gibt 16 Unentschieden-Positionen, die aus folgenden drei durch Spiegelung oder Rotation erhalten werden können:
Meist setzt der erste Spieler (X) in die Mitte. Der zweite Spieler muss, um ein Unentschieden zu erzwingen, in die Ecke setzen, sonst kann Spieler 1 mühelos einen Sieg erringen:
Weitere Informationen
Tic Tac Toe war auch eines der ersten Spiele, die auf Computern (bereits vor Tennis for Two, 1958) erschienen (Spiel OXO auf einem EDSAC-Computer, 1952). Allerdings ist dieses eher ein textbasiertes (nicht grafisches) Spiel.
Eine entscheidende Rolle spielt Tic Tac Toe auch im Film Wargames.
Siehe auch
Literatur
- Norman Do: How to Win at TicTacToe (PDF), The Australian Mathematical Society, Gazette, Volume 32 Number 3, July 2005, p.151
Weblinks
 Commons: Tic Tac Toe – Sammlung von Bildern, Videos und Audiodateien
Commons: Tic Tac Toe – Sammlung von Bildern, Videos und Audiodateien- Folge A008907 in OEIS (englisch; Anzahl der möglichen Stellungen im Spielverlauf bis auf Rotation oder Spiegelung)
- Tic Tac Toe Browserspiel Tic Tac Toe im Webbrowser ausprobieren
- (englisch) Anleitung zum Spiel ohne Niederlage
Kategorien:- Papier-und-Bleistift-Spiel
- Gelöstes Spiel
Wikimedia Foundation.