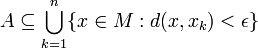Totalbeschränkt

Im mathematischen Teilgebiet der Topologie ist Totalbeschränktheit eine bestimmte Endlichkeitsbedingung an einen metrischen Raum. Es ist schwierig, globale Eigenschaften eines metrischen Raumes zu erfassen, weil man eine Metrik stets durch eine äquivalente Metrik ersetzen kann, mit der der Raum endlichen Durchmesser hat. Der Begriff der Totalbeschränktheit umgeht dieses Problem, indem er stattdessen fordert, dass man den Raum in endlich viele Stücke unterteilen kann, von denen jedes eine vorgegebene Größe nicht überschreitet.

Definition

Eine Teilmenge A eines metrischen Raumes 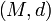$\left(M, d\right)$ heißt totalbeschränkt (oder auch präkompakt), wenn es zu jedem ε > 0 eine endliche Menge von Punkten 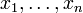$x_1,\ldots,x_n$ (ein ε-Netz) gibt, so dass

$A\subseteq\bigcup_{k=1}^n\{x\in M:d(x,x_k)<\epsilon\}$

gilt. Das heisst, die Teilmenge A wird für jedes ε > 0 von endlich vielen ε-Kugeln überdeckt.

Äquivalente Definition

Es lässt sich zeigen, dass ein metrischer Raum genau dann totalbeschränkt ist, wenn jede Folge eine Teilfolge besitzt, die eine Cauchy-Folge ist.

Eigenschaften

Die hauptsächliche Bedeutung des Begriffes der Totalbeschränktheit liegt in der folgenden Aussage:

Ein metrischer Raum ist genau dann kompakt, wenn er vollständig und totalbeschränkt ist.

Dies ist in gewisser Weise eine Verallgemeinerung des Satzes von Heine-Borel, der aussagt, dass eine Teilmenge des 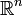$\mathbb{R}^{n}$ genau dann kompakt ist, wenn sie abgeschlossen und beschränkt ist.

Verallgemeinerung auf uniforme Räume

Wie viele andere Begriffe aus der Theorie metrischer Räume, lässt sich auch der Begriff "totalbeschränkt", bzw. "präkompakt" verallgemeinern auf die Klasse der uniformen Räume:

Eine Teilmenge A eines uniformen Raumes 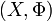$\left(X, \Phi\right)$ heißt dann präkompakt, wenn es zu jedem 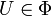$U\in \Phi$ eine endliche Menge von Punkten 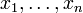$x_1,\ldots,x_n$ gibt, so dass

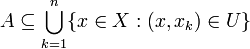$A\subseteq\bigcup_{k=1}^n\{x\in X:(x,x_k)\in U\}$ gilt.

Äquivalent ist, dass jedes Netz ein Cauchy-Teilnetz besitzt.

Eine weitere Verallgemeinerung auf beliebige topologische Räume ist allerdings nicht möglich. Totalbeschränktheit, bzw. Präkompaktheit ist somit keine topologische Eigenschaft.