- Umordnung
-
Die Umordnung von Reihen wird in der Mathematik beim Studium der Konvergenz von unendlichen Summen, sogenannten Reihen, untersucht. Es geht dabei um die Frage, welche Grenzwerte der Reihen sich durch Umordnung der Summanden, d.h. durch Änderung ihrer Reihenfolge, ergeben können. Im Falle reeller Reihen gibt der riemannsche Umordnungssatz Auskunft über die möglichen Reihensummen; die Situation in endlich-dimensionalen Vektorräumen wird im steinitzschen Umordnungssatz erschöpfend behandelt.
Viele Aussagen über konvergente Reihen in endlich-dimensionalen Räumen verlieren in unendlich-dimensionalen Räumen ihre Gültigkeit. Verallgemeinerungen des steinitzschen Umordnungssatzes erhält man nur unter zusätzlichen Voraussetzungen. Der Schwerpunkt dieses Artikels ist die Umordnung von Reihen in unendlich-dimensionalen Räumen. Daher spielen hier, im Gegensatz zum riemannschen und steinitzschen Umordnungssatz, die der klassischen Analysis zuzurechnen sind, funktionalanalytische Methoden und Begriffsbildungen eine wichtige Rolle.
Inhaltsverzeichnis
Konvergenzbegriffe
Es sei
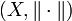 ein Banachraum. Eine Reihe
ein Banachraum. Eine Reihe 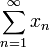 in X heißt konvergent, wenn die Folge der Partialsummen
in X heißt konvergent, wenn die Folge der Partialsummen 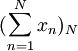 konvergiert. Die Reihe heißt unbedingt konvergent, wenn
konvergiert. Die Reihe heißt unbedingt konvergent, wenn 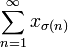 für jede Permutation
für jede Permutation  konvergiert, d.h. wenn jede Umordnung der Reihe konvergiert. Man spricht von perfekter Konvergenz, falls
konvergiert, d.h. wenn jede Umordnung der Reihe konvergiert. Man spricht von perfekter Konvergenz, falls 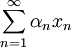 für jede Wahl
für jede Wahl 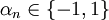 konvergiert, d.h. die Reihe konvergiert bei jeder Wahl von Vorzeichen der Summanden. Die Reihe heißt absolut konvergent, falls
konvergiert, d.h. die Reihe konvergiert bei jeder Wahl von Vorzeichen der Summanden. Die Reihe heißt absolut konvergent, falls 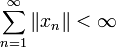 .
.Problemstellung
Für eine Folge (xn)n in X sei
 die Menge aller Summen, die man durch Umordnung der Reihe
die Menge aller Summen, die man durch Umordnung der Reihe 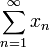 erhalten kann, kurz die Summenmenge der Folge. Es stellt sich die Frage, was über die Struktur dieser Menge gesagt werden kann.
erhalten kann, kurz die Summenmenge der Folge. Es stellt sich die Frage, was über die Struktur dieser Menge gesagt werden kann.Der endlich-dimensionale Fall
Der endlich-dimensionale Falle wird erschöpfend durch den steinitzschen Umordnungssatz behandelt. Für eine Folge (xn)n sei
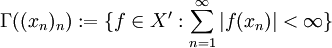 der Unterraum der sogenannten Konvergenzfunktionale. Ist die Reihe Σxn konvergent, so ist
der Unterraum der sogenannten Konvergenzfunktionale. Ist die Reihe Σxn konvergent, so ist 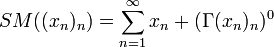 , wobei (Γ(xn)n)0 die Menge aller
, wobei (Γ(xn)n)0 die Menge aller  sei, für die f(x) = 0 für alle
sei, für die f(x) = 0 für alle 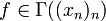 gilt. Insbesondere ist SM((xn)n) stets ein affiner Unterraum.
gilt. Insbesondere ist SM((xn)n) stets ein affiner Unterraum.Ferner sind für eine Reihe
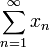 in einem endlich-dimensionalen Raum folgende Aussagen äquivalent:
in einem endlich-dimensionalen Raum folgende Aussagen äquivalent:- Die Reihe konvergiert absolut.
- Die Reihe konvergiert unbedingt.
- Die Reihe konvergiert perfekt.
- SM(xn)n ist einelementig.
In Bezug auf obige Problemstellung stellt sich die Frage, ob diese Aussagen auch in unendlich-dimesionalen Räumen Gültigkeit behalten.
Das Problem 106
Die Frage nach der Struktur der Summenmenge in unendlich-dimensionalen Räumen wurde erstmalig 1935 von Stefan Banach als Problem 106 im sogenannten schottischen Buch gestellt. Dabei handelt es sich um eine im Schottischen Café zu Lemberg aufbewahrte Kladde, in der die Lemberger Funktionalanalytiker und ihre Gäste mathematische Probleme festhielten. Stefan Banach trug dort die Vermutung ein, dass die Summenmenge stets affin sei, und versprach für die Klärung der Frage eine Flasche Wein, derartige Preise waren für hier gestellte Probleme durchaus üblich. Im schottischen Buch findet sich ohne Angabe eines Autors bereits ein Gegenbeispiel zu dieser Vermutung, Józef Marcinkiewicz gilt nach einer Handschriftenanalyse als wahrscheinlicher Urheber.
Mit diesem Gegenbeispiel war klar, dass eine zum steinitzschen Umordnungssatz analoge Aussage im unendlich-dimensionalen Fall nicht zutrifft. Die damals bekannten Beispiele waren so konstruiert, dass die Summenmenge immerhin noch eine um einen konstanten Vektor verschobene Untergruppe der additiven Gruppe des Banachraums war. Erst 1989 konnten M. I. Kadets und Krzysztof Wozniakowski und unabhängig davon P. A. Kornilow Beispiele von Reihen angeben, für die die Summenmenge keine verschobene Untergruppe ist. Es hat sich herausgestellt, dass es in jedem unendlich-dimensionalen Banachraum Reihen mit zweielementiger Summenmenge gibt. Damit hat sich die im Problem 106 des schottischen Buches geäußerte Vermutung als dramatisch falsch erwiesen.
Weitere negative Aussagen
In endlich-dimensionalen Räumen sind Summenmengen als affine Unterräume stets abgeschlossen. Auch diese Eigenschaft gilt in unendlich-dimensionalen Räumen im Allgemeinen nicht mehr, wie M. I. Ostrowskii 1986 zeigen konnte.
Auch die Äquivalenz zwischen absoluter Konvergenz und unbedingter Konvergenz geht in unendlich-dimensionalen Räumen verloren, denn es gilt folgender Satz von Dvoretzky-Rogers:
- Sei X ein unendlich-dimensionaler Banachraum. Weiter seien αn > 0 mit
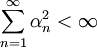 . Dann gibt es eine unbedingt konvergente Reihe
. Dann gibt es eine unbedingt konvergente Reihe 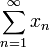 mit
mit 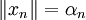 für alle n.
für alle n.
Wählt man speziell
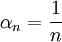 , so liefert dieser Satz die Existenz einer unbedingt konvergenten Reihe, deren Summanden die Norm
, so liefert dieser Satz die Existenz einer unbedingt konvergenten Reihe, deren Summanden die Norm  haben. Diese Reihe ist daher nicht absolut konvergent.
haben. Diese Reihe ist daher nicht absolut konvergent.Positive Ergebnisse
Trotz der obigen Liste negativer Resultate können auch einige positive Ergebnisse vermerkt werden. Aus der absoluten Konvergenz folgt auch in unendlich-dimensionalen Räumen die unbedingte Konvergenz und diese ist äquivalent zur perfekten Konvergenz. Ferner ist die Summenmenge einer unbedingt konvergenten Reihe stets einelementig.
Stellt man zusätzliche Voraussetzungen an die Reihe oder betrachtet man spezielle Räume, so kann man Verallgemeinerungen des steinitzschen Umordnungssatz beweisen:
- Sei
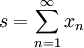 eine konvergente Reihe in Lp[0,1] ,
eine konvergente Reihe in Lp[0,1] , 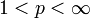 , und es sei
, und es sei 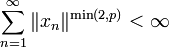 . Dann ist SM((xn)n) = s + Γ((xn)n)0.
. Dann ist SM((xn)n) = s + Γ((xn)n)0. - D. V. Pecherskii (1988): Sei
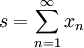 eine konvergente Reihe in einem Banachraum. Zu jeder Umordnung
eine konvergente Reihe in einem Banachraum. Zu jeder Umordnung  gebe es
gebe es 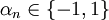 , so dass
, so dass 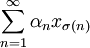 konvergiert. Dann ist SM((xn)n) = s + Γ((xn)n)0.
konvergiert. Dann ist SM((xn)n) = s + Γ((xn)n)0.
In eine ganz andere Richtung zielt ein Ergebnis von Wojciech Banaszczyk. Man kann Klassen lokalkonvexer Räume definieren, die sehr viel mehr Eigenschaften mit endlich-dimensionalen Räumen gemeinsam haben als Banachräume, das gilt insbesondere für Kompaktheitseigenschaften. Daher kann man hoffen, in solchen Raumklassen Verallgemeinerungen des steinitzschen Umordnungssatzes zu erhalten, und in der Tat gilt folgender Satz:
- Sei
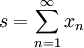 eine konvergente Reihe in einem metrisierbaren, nuklearen Raum. Dann ist SM((xn)n) = s + Γ((xn)n)0.
eine konvergente Reihe in einem metrisierbaren, nuklearen Raum. Dann ist SM((xn)n) = s + Γ((xn)n)0.
Siehe auch
Quellen
- W. Banaszczyk: The Steinitz theorem on rearrangement of series for nuclear spaces. Journal für die reine und angewandte Mathematik 403 (1990), 187-200.
- M. I. Kadets, V. M. Kadets: Series in Banach Spaces. Operator Theory: Advances and Applications, Bd. 94, Birkhäuser (1997), ISBN 978-3764354015.
- M. I. Kadets, K. Wozniakowski: On Series Whose Permutations Have Only Two Sums. Bull. Polish Acad. Sciences Mathematics 37 (1989), 15-21.
- P. A. Kornilow: On the Set of Sums of a Conditionally Convergent Series of Functions. Math USSR Sbornik 65, No 1 (1990), 119-131.
- M. I. Ostrowskii: Domains of Sums of Conditionally Convergent Series in Banch Spaces. Teor. Funktsii Funktional. Anal. i Prilozhen 46 (1986), 77-85.
Wikimedia Foundation.
