Unvollständige LU-Zerlegung

Als ILU-Zerlegung (von incomplete LU-Decomposition) oder unvollständige LU-Zerlegung bezeichnet man in der numerischen Mathematik die fehlerbehaftete Zerlegung einer Matrix 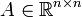$A \in \mathbb{R}^{n\times n}$ in das Produkt einer unteren Dreiecksmatrix L und einer oberen Dreiecksmatrix U

$LU\approx A$,

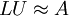bei der von den Zerlegungsmatrizen L und U nur die Einträge einer vorgegebenen Besetzungsstruktur berechnet werden.

Die ILU-Zerlegung wird erfolgreich als Vorkonditionierer zur Beschleunigung der iterativen Lösung großer dünnbesetzter linearer Gleichungssysteme Ax = b mittels Krylow-Unterraum-Verfahren eingesetzt. Es werden dabei keine Eigenschaften des eigentlichen Problems (meist die numerische Lösung einer partiellen Differentialgleichung) ausgenutzt. Damit ist sie nicht auf bestimmte Problemklassen beschränkt und hat Einzug in viele Bereiche der numerischen Simulation gefunden, beispielsweise in der numerischen Strömungsmechanik ist die Technik weit verbreitet.

Zuerst erwähnt wurde das Verfahren 1960 von Varga^[1] und Buleev.^[2] Eine genauere Analyse wurde 1977 von Meijerink und van der Vorst veröffentlicht. Diese untersuchten Vorkonditionierungstechniken für das CG-Verfahren und schlugen eine unvollständige Cholesky-Zerlegung für symmetrische Matrizen vor. Gleichzeitig erwähnten sie eine Erweiterung auf allgemeine Matrizen.^[3]

Bei der Berechnung einer normalen LU-Zerlegung einer dünnbesetzten Matrix kann man die Besetzungsstruktur in der Regel nicht ausnutzen. Es wird daher sehr viel mehr Speicherplatz benötigt als für die ursprüngliche Matrix und auch die Anzahl der notwendigen Rechenoperationen ist nicht geringer als die für eine vollbesetzte Matrix. Durch die Vorgabe einer maximalen Besetzungsstruktur wird dieses Problem auf Kosten einer fehlerbehafteten Zerlegung umgangen.

Anwendung

Für die Anwendung als Vorkonditionierer wird das Gleichungssystem Ax = b formal mit (LU) ^{− 1} multipliziert,

(LU) ^{− 1}Ax = (LU) ^{− 1}b.

Wendet man darauf Krylow-Unterraum-Verfahren an, so konvergieren diese besser, da die Matrix (LU) ^{− 1}A näher an der Einheitsmatrix als A ist. Für diese Verfahren benötigt man in jedem Schritt Matrix-Vektor-Multiplikationen. Da A schwach besetzt ist, ist die Berechnung von y = Ax mit geringem Rechenaufwand möglich. Für die Lösung von c = (LU) ^{− 1}y kann man das äquivalente Gleichungssystem

LUc = y

effizient durch Vorwärts-Rückwärts-Einsetzen lösen. Dabei lässt sich die schwache Besetztheit der Matrizen L und U ausnutzen.

Die Berechnung einer ILU-Zerlegung ist, etwa im Vergleich zu Splitting-basierten Vorkonditionierern wie Gauß-Seidel, relativ aufwändig, wobei der Aufwand direkt mit der Größe der erlaubten Besetzungsstruktur zusammenhängt. Aufgewogen wird dies durch die Beschleunigung der Krylow-Unterraum-Verfahren, die in der Regel besser ist, je größer die erlaubte Besetzungsstruktur. Werden direkt hintereinander mehrere Systeme mit derselben Matrix, aber verschiedenen rechten Seiten gelöst, empfiehlt es sich somit, mehr in die Berechnung der ILU zu investieren. Bei der numerischen Lösung zeitabhängiger partieller Differentialgleichungen, bei denen häufig Sequenzen tausender ähnlicher linearer Gleichungssysteme nacheinander zu lösen sind, wird eine einmal berechnete ILU-Zerlegung in der Regel eingefroren und periodisch neuberechnet.

ILU-Zerlegungen oder Varianten sind Teil jeder größeren Programmbibliothek zur Lösung dünnbesetzter linearer Gleichungssysteme, etwa von PetSc oder von MATLAB.

Grundform

In der Grundform wird als Besetzungsstruktur P die von A vorgegeben. Die Zerlegung in die Matrizen L und U wird dann durch folgende Bedingungen definiert:

1. $u_{ii}=1, \, i=1,...,n$,
2. $l_{ij} = u_{ij} =0, \mbox{falls} (i,j) \notin P$
3. $(LU)_{ij} = a_{ij}, \mbox{falls} (i,j) \in P.$

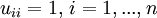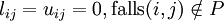
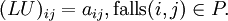
Da für 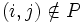$(i,j)\notin P$ nicht (LU)_ij = 0 gefordert wird, ist 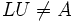$LU \neq A$ möglich (dies motiviert noch einmal den Namen unvollständige LU-Zerlegung).

Gegeben ist die $n \times n$-Matrix A = (a_ij). Die unvollständigen Zerlegungsmatrizen L und U werden dann gemeinsam in einer neuen Matrix M = (m_ij) abgespeichert, wobei die bereits vorher bekannten Einsen auf der Diagonale von L nicht gespeichert werden. Die Matrix M wird derart initialisiert, dass sie für Einträge aus P identisch zu A gesetzt wird, andernfalls zu Null. Die Berechnung der Zerlegung erfolgt dann mittels des folgenden Algorithmus:

For k = 1,...,n − 1, do
   For i = k + 1,...,n and if $(i,k) \in P$, do
      mik: = mik / mkk
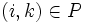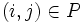      For j = k + 1,...,n and if $(i,j) \in P$, do
         mij: = mij − mikmkj

Die Reihenfolge der Schleifen im obigen Algorithmus kann verändert werden, um je nach Datenstruktur die Effizienz zu verbessern. Wird die Matrix beispielsweise zeilenweise abgespeichert, geschehen die Speicherzugriffe in der letzten Schleife nicht auf benachbarte Speicherblöcke. In solchen Fällen ist dann eine Vertauschung von Schleifen sinnvoll.

Existenz

Existenzaussagen der Zerlegung gibt es für M-Matrizen und H-Matrizen. Für allgemeine Matrizen gibt es Gegenbeispiele, bei denen der Algorithmus vorzeitig terminiert, weil eine Null auf der Diagonalen auftaucht, was zu einer Division durch Null führt. Trotzdem ist in der Praxis ein Abbrechen der Berechnung der Zerlegung nicht zu beobachten.

Varianten

Es gibt viele Varianten der ursprünglichen ILU-Zerlegung. Diese versuchen, entweder die Approximationseigenschaften zu verbessern oder bei ähnlicher Approximationsgüte den Berechnungsaufwand zu verkleinern.

ILU(p)

Weit verbreitet sind die ILU(p)-Zerlegungen, die erstmals von Watts 1981 bei der Simulation eines Ölreservoirs betrachtet wurden. Hierbei bezeichnet p den Level of Fill. Die Basisversion der ILU hat den Level 0. Der Level 1 wird dadurch definiert, dass die Besetzungsstruktur des Produkts der Matrizen L und U aus der ILU(0) betrachtet wird. Level 2 ergibt sich aus den Zerlegungsmatrizen von ILU(1) usw. Zur Bestimmung der Besetzungsstruktur einer ILU(p)-Zerlegung ist es nicht nötig, die Zerlegungen der unteren Level vorab zu berechnen. Dazu weist man den Nichtnulleinträgen der Matrix A anfangs den Level 0 zu, den Nulleinträgen dagegen unendlich. Dann durchläuft man die Elemente der Matrix so, wie es im regulären Algorithmus passieren würde und jedes Mal, wenn das Element a_ij in der innersten Schleifen modifiziert werden würde, wird der Level aufdatiert mittels

lev_ij = min(lev_ij,lev_ik + lev_kj + 1).

Somit ist es möglich, den Speicher für die ILU-Zerlegung vor Start des Algorithmus bereitzustellen. Bei der Benutzung einer ILU(p) ist zu beachten, dass zum Einen die Berechnung der Zerlegung aufwändiger ist als bei der Basisversion und ferner die Anwendung teurer, da der Vorkonditionierer mehr Nichtnulleinträge hat. Damit führen bei hohen Levels etwa ab 3 die Reduktionen der Iterationszahlen im Krylow-Unterraum-Verfahren nicht mehr notwendigerweise zu einer Verkürzung der CPU-Zeiten. Darüber hinaus kann es vor allem bei indefiniten Matrizen sogar zu einer Verschlechterung der Iterationszahlen im Vergleich zur Basisversion kommen.

ILUT

Die ILU(p) haben den Nachteil, dass die Nichtnulleinträge nicht aufgrund von Approximationseigenschaften gewählt werden und somit Rechenzeit für Fast-Nulleinträge vergeudet werden kann. Dies wird in der 1994 von Yousef Saad vorgeschlagenen ILU-Zerlegung mit Threshold, genannt ILUT, berücksichtigt. Hier werden neben dem Einsatz einer Besetzungsstruktur noch zusätzliche Bedingungen zugelassen, nach denen Einträge nicht berücksichtigt werden, falls sie unterhalb einer gewissen Toleranz sind. Etwa für bestimmte diagonaldominante M-Matrizen kann dann wieder die Existenz der Zerlegung bewiesen werden. Die Implementierung einer effizienten ILUT ist schwieriger als bei den anderen Varianten, dafür sind häufig höhere Levels of Fill möglich als bei einer reinen ILU(p).

Weitere Varianten

Die ILU ist ohne große Probleme auf Blockmatrizen erweiterbar, hierbei muss statt der Division durch das Diagonalelement d_ii mit der Inversen des entsprechenden Diagonalblocks multipliziert werden.

Vergleich von ICCG mit CG anhand der 2D-Poisson-Gleichung

Ein Spezialfall ist dagegen die unvollständige Cholesky-Zerlegung (IC). Diese wendet das Konzept der ILU-Zerlegung auf symmetrische und positiv definite Matrizen an, analog zur Cholesky-Zerlegung. Dieses 1977 als erste ILU-Variante eingeführte Verfahren wird häufig als Vorkonditionierer für das CG-Verfahren eingesetzt. Die Kombination CG mit IC wird auch als ICCG bezeichnet.

Parallelisierung

Die ILU-Zerlegung ist streng sequentiell und daher schwer parallelisierbar. Allerdings wurden Varianten entwickelt, die die zentralen Ideen nutzen, um Parallelisierung möglich zu machen. Hierzu gehören insbesondere Multilevel-Techniken wie ILUM. Dabei werden unabhängige Mengen genutzt, um einen Satz Unbekannte blockweise zu eliminieren. Der entstehende Fill-In wird durch einen Threshold begrenzt. Daraufhin wird in den verbleibenden Unbekannten eine neue unabhängige Menge gesucht und der Schritt wiederholt, bis der verbleibende Block klein genug für eine direkte Lösung geworden ist.

Einfluss der Nummerierung

Die Nummerierung der Unbekannten in A hat einen nicht zu unterschätzenden Einfluss auf die Effizienz des Vorkonditionierers. Dies liegt daran, dass der Fill-In in der exakten Zerlegung genau davon abhängt und damit die Nummerierung Einfluss darauf hat, wie gut die fehlerbehaftete ILU-Zerlegung A approximiert. Darüber hinaus beeinflusst die Nummerierung die Größe der Einträge auf der Diagonalen und damit die Stabilität.

Auch hier gibt es keine handfesten Aussagen, welche Nummerierung für welche Art von Problemen sinnvoll ist. Insbesondere bei Verwendung der Grundversion ILU(0) sind keine überzeugenden Heuristiken bekannt. Für die stärkeren Vorkonditionierer ILUT oder ILU(p) mit p>0 hat sich in vielen Fällen die Reverse-Cuthill-McKee-Nummerierung als günstig herausgestellt.

Literatur

• Andreas Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7
• Gerard Meurant: Computer Solution of Large Linear Systems, Elsevier, 1999, ISBN 0-444-50169-X
• Yousef Saad: Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM Society for Industrial & Applied Mathematics 2003, ISBN 0-898-71534-2

Einzelnachweise

1. ↑ Varga R.S.: Factorization and normalized iterative methods In: Boundary problems in differential equations (Hrsg.: R.E.Langer) University of Wisconsin Press, Madison 1960
2. ↑ Eine numerische Methode zur Lösung zwei- und dreidimensionaler Diffusionsgleichungen Math.Sb. 51(1960)
3. ↑ Meijerink, van der Vorst: An iterative solution method for linear systems of which the coefficients matrix is a symmetric M-Matrix, Mathematics of Computation 31 (1977), pp. 148–162