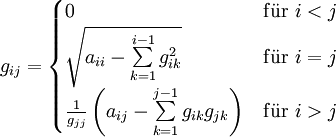Cholesky-Verfahren

Die Cholesky-Zerlegung (nach André-Louis Cholesky (1875-1918)) bezeichnet in der numerischen Mathematik eine Zerlegung einer symmetrischen positiv definiten Matrix.

Einsatzbereiche

Bei der Anwendung der Methode der kleinsten Quadrate ist eine Möglichkeit, in jedem Schritt die Normalgleichungen zu lösen, die eine symmetrisch positiv definite Matrix haben. Dies ist mit Hilfe der Cholesky-Zerlegung möglich und dies war die Motivation von Cholesky, die Zerlegung zu entwickeln. Beim Gauß-Newton-Verfahren ist damit bei jedem Iterationsschritt ein Gleichungssystem zu lösen, das sich mit dem Cholesky-Verfahren bestimmen lässt.

Die Cholesky-Zerlegung kann auch zur Gewinnung eines Vorkonditionierungsverfahrens für lineare Gleichungssysteme mit positiv definiter Matrix benutzt werden; zu diesem Zweck gibt es speziell die Variante der unvollständigen Cholesky-Zerlegung sowie der modifizierten unvollständigen Cholesky-Zerlegung.

Gleichzeitig stellt die Zerlegung einen Test dar, ob eine gegebene symmetrische Matrix positiv definit ist. Andernfalls ist einer der Einträge auf der Diagonalen negativ, so dass die Wurzel nicht gezogen werden kann, oder Null, so dass nicht durch den Eintrag geteilt werden kann. In beiden Fällen bricht der Algorithmus ab. Die Cholesky-Zerlegung lässt sich auch zur Bestimmung der Determinanten der Matrix A verwenden, denn es gilt $\det A = \prod_{i=1}^n G_{ii}^2$.

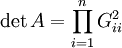Außerhalb der Mathematik findet die Cholesky-Zerlegung auch Anwendung in der ökonometrischen Erforschung makroökonomischer Zusammenhänge. Hierbei wird bei sogenannten vektorautoregressiven Modellen (VAR) die Reihenfolge der Beeinflussung der endogenen Variablen untereinander festgelegt.

Darüber hinaus wird sie auch bei der Monte-Carlo-Simulation eingesetzt, um vorgegebene Korrelationen in unabhängig generierte Zufallszahlenfolgen (als Diskretisierung stochastischer Prozesse) zu bringen.

Formulierung und Anwendung

Jede symmetrische positiv definite Matrix 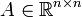$A \in \mathbb{R}^{n\times n}$ kann eindeutig in der Form

A = LDL^T

geschrieben werden. Dabei ist L eine untere Dreiecksmatrix, deren Diagonalelemente alle gleich 1 sind und D eine Diagonalmatrix mit positiven Einträgen. Mit der Matrix-"Wurzel" von D und dem Matrix-Faktor G, definiert durch

D = D^{1 / 2}D^{1 / 2}

und

G: = LD^{1 / 2},

wird die Cholesky-Zerlegung – äquivalent – auch formuliert als

A = GG^T.

Liegt eine Berechnung der Cholesky-Zerlegung vor, so lässt sich das Gleichungssystem Ax = b effizient durch Vorwärts- und Rückwärtseinsetzen lösen:

• Durch Vorwärtseinsetzen Lösung des linearen Gleichungssystems Gy = b

• Durch anschließendes Rückwärtseinsetzen Lösung des linearen Gleichungssystems G^Tx = y.

Berechnung

Setzt man A = GG^T so erhält man für die Elemente von A:

$a_{ij}=\sum\limits_{k=1}^jg_{ik} g_{jk} \quad i\ge j$

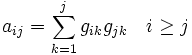
Dieser Zusammenhang führt direkt auf die folgenden Formeln.

$g_{ij} = \begin{cases}0 & \mathrm{f\ddot{u}r}\ i < j\\ \sqrt{a_{ii} - \sum\limits_{k=1}^{i-1}g_{ik}^2 } & \mathrm{f\ddot{u}r}\ i = j\\ \frac{1}{g_{jj}} \left( a_{ij}-\sum\limits_{k=1}^{j-1}g_{ik} g_{jk} \right) & \mathrm{f\ddot{u}r}\ i > j \end{cases}$

Aufwand und Stabilität

Die Cholesky-Zerlegung ist numerisch stabil. Den Aufwand der Berechnung betreffend muss sie mit dem Eliminationsverfahren nach Gauß und seiner algorithmischen Umsetzung, der LR-Zerlegung, verglichen werden. Letzteres erfordert etwa doppelt so viele Operationen, da nicht nur eine Matrix G, sondern zwei Faktoren L und R berechnet werden müssen. Bei der Cholesky-Zerlegung treten ungefähr 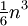$\tfrac{1}{6}n^3$ Multiplikationen, Divisionen und Wurzeloperationen auf.^[1]

Pseudocode

In Pseudocode sieht das Cholesky-Verfahren zur Zerlegung der Matrix A in die Form GG^T so aus:

   For i = 1 To n
       For j = 1 To i-1
           Summe = a(i, j)
           For k = 1 To j-1
               Summe = Summe - a(i, k) * a(j, k)
           Next k
           a(i, j) = Summe / a(j, j)
       Next j
       Summe = a(i, i)
       For k = 1 To i-1
           Summe = Summe - a(i, k) * a(i, k)
       Next k
       If Summe <= 0 Then 
           EXIT                  // A ist nicht positiv definit
       else 
           a(i, i) = Sqrt(Summe) // Summe ist positiv
       End If
   Next i

Die Indizes der Matrix A entsprechen der mathematischen Notierung i=1..n, j=1..n, n ist die Anzahl der Zeilen und gleichzeitig die Anzahl der Spalten der Matrix A, Hilfsvariablen sind i, j, k und Summe. Der Algorithmus arbeitet in-place, d.h. er modifiziert die Matrix A so, dass sie die untere Dreiecksmatrix G enthält.

Der Algorithmus bearbeitet nur die linke untere Dreiecksmatrix von A, die Werte a_i,j für i < j brauchen nicht mit Werten belegt zu werden (da die Matrix A nach Voraussetzung symmetrisch ist) und wenn sie Werte enthalten, werden diese nicht verändert. Sucht man also nach der Cholesky-Zerlegung G gemäß A = G^TG, so sind die Matrixelemente von A oberhalb der Diagonalen (i < j) gleich Null zu setzen.

Literatur

• Hans Rudolf Schwarz & Nobert Köckler: Numerische Mathematik. Stuttgart: Teubner, 2004 (5. Auflage) ISBN 3-519-42960-8
• Gene H. Golub & Charles F. Van Loan: Matrix computations. Johns Hopkins University Press, 1996 (3rd edition) ISBN 0-80185414-8

Einzelnachweise

1. ↑ Andreas Meister: Numerik linearer Gleichungssysteme. 2. Auflage. Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7, S. 46