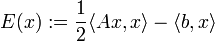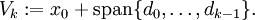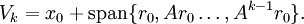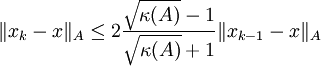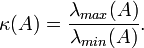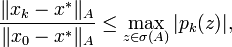- Methode der konjugierten Gradienten
-
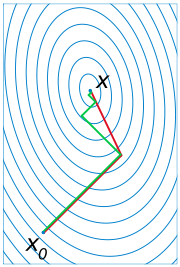 Ein Vergleich des einfachen Gradientenverfahren mit optimaler Schrittlänge (in grün) mit dem CG-Verfahren (in rot) für die Minimierung der quadratischen Form eines gegebenen linearen Gleichungssystems. CG konvergiert nach 2 Schritten, die Größe der Systemmatrix ist m=2).
Ein Vergleich des einfachen Gradientenverfahren mit optimaler Schrittlänge (in grün) mit dem CG-Verfahren (in rot) für die Minimierung der quadratischen Form eines gegebenen linearen Gleichungssystems. CG konvergiert nach 2 Schritten, die Größe der Systemmatrix ist m=2).Das CG-Verfahren (von engl. conjugate gradients oder auch Verfahren der konjugierten Gradienten) ist eine effiziente numerische Methode zur Lösung von großen, symmetrischen, positiv definiten Gleichungssystemen der Form Ax = b. Es gehört zur Klasse der Krylow-Unterraum-Verfahren. Das Verfahren konvergiert nach spätestens m Schritten, wobei m die Dimension der quadratischen Matrix A ist. Insbesondere ist es aber als iteratives Verfahren interessant, da der Fehler monoton fällt.
Inhaltsverzeichnis
Idee des CG-Verfahrens
Die Idee des CG-Verfahrens besteht darin, dass das Minimieren von
äquivalent zum Lösen von Ax = b ist. Hierbei bezeichnet
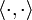 das euklidische Skalarprodukt.
das euklidische Skalarprodukt.Der Gradient von E an der Stelle xk ist gerade rk = Axk − b und somit bei großen, dünn besetzten Matrizen schnell zu berechnen. Die Idee des CG-Verfahrens ist es nun, anstelle in Richtung rk wie beim Verfahren des steilsten Abstiegs in eine andere Richtung dk die Funktion E über einen Unterraum zu minimieren. Die Richtungen dk sind dabei alle A-konjugiert, das heißt es gilt
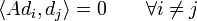 .
.
Die Iterierten xk des CG-Verfahrens werden dann so gewählt, dass sie das Minimum von E in dem affinen Raum Vk, der durch die Vektoren
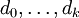 aufgespannt und um x0 verschoben wird, bilden:
aufgespannt und um x0 verschoben wird, bilden:Es lässt sich zeigen, dass ebenfalls gilt:
Der letzte Teil zeigt, dass die Suchrichtungen den Krylow-Unterraum zu A und r0 aufspannen. Das CG-Verfahren lässt sich deswegen alternativ direkt als Krylow-Unterraum-Verfahren definieren.
Da die Vektoren dk alle A-konjugiert sind, ist die Dimension von Vk gerade k. Ist also A eine
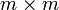 -Matrix, so terminiert das Verfahren nach spätestens m Schritten, falls exakt gerechnet wird. Numerische Fehler können durch weitere Iterationen eliminiert werden. Hierzu betrachtet man den Gradienten rk, der das Residuum angibt. Unterschreitet die Norm dieses Residuums einen gewissen Schwellenwert, wird das Verfahren abgebrochen.
-Matrix, so terminiert das Verfahren nach spätestens m Schritten, falls exakt gerechnet wird. Numerische Fehler können durch weitere Iterationen eliminiert werden. Hierzu betrachtet man den Gradienten rk, der das Residuum angibt. Unterschreitet die Norm dieses Residuums einen gewissen Schwellenwert, wird das Verfahren abgebrochen.Das Verfahren baut sukzessive eine A-orthogonale Basis für den
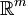 auf und minimiert in die jeweilige Richtung bestmöglich.
auf und minimiert in die jeweilige Richtung bestmöglich.Das Problem bei dem iterativen Verfahren ist das Finden der optimalen Schrittweite. Um die Güte eines Punktes zu bestimmen ist jeweils eine vollständige Matrixmultiplikation notwendig, welche nebenbei gleich einen neuen Gradienten liefert. Ist die Schrittweite entlang eines vorgegebenen Gradienten zu ungenau, entspricht die Methode eher einem einfachen Downhill-Algorithmus.
Varianten
Es existieren verschiedene Varianten des Verfahrens, z. B. Fletcher-Reeves, Hestenes-Stiefel, Davidon-Fletcher-Powell und Polak-Ribiere.
- βk + 1 = (gk + 1)Tgk + 1 / (gk)Tgk (Fletcher-Reeves)
- βk + 1 = (gk + 1)T(gk + 1 − gk) / (gk)Tgk (Polak-Ribiere)
- βk + 1 = (gk + 1)T(gk + 1 − gk) / (dk)T(gk + 1 − gk) (Hestenes-Stiefel)
CG-Verfahren ohne Vorkonditionierung
Zunächst wählt man ein
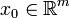 beliebig und berechnet:
beliebig und berechnet:- r0 = b − Ax0
- d0 = r0
Für k = 0,1,... setzt man:
Finde von xk in Richtung dk das Minimum xk + 1 und aktualisiere den Gradienten bzw. das Residuum
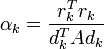
- xk + 1 = xk + αkdk
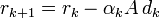
Korrigiere die Suchrichtung dk + 1 mit Hilfe von dk und rk + 1
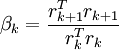
- dk + 1 = rk + 1 + βkdk
bis das Residuum in der Norm kleiner als eine Toleranz ist (
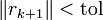 ).
).CG-Verfahren mit symmetrischer Vorkonditionierung (PCG-Verfahren)
Die Konvergenz des CG-Verfahren ist nur bei symmetrischen positiv definiten Matrizen gesichert. Dies muss ein Vorkonditionierer berücksichtigen. Bei einer symmetrischen Vorkonditionierung wird das Gleichungssystem Ax = b mit Hilfe einer Vorkonditionierer-Matrix
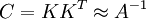 zu KTAKy = KTb mit y = K − 1x transformiert, und darauf das CG-Verfahren angewandt.
zu KTAKy = KTb mit y = K − 1x transformiert, und darauf das CG-Verfahren angewandt.Die Matrix KTAK ist symmetrisch, da A symmetrisch ist. Sie ist ferner positiv definit, da nach dem Trägheitssatz von Sylvester A und KTAK die gleichen Anzahlen positiver und negativer Eigenwerte besitzen.
Das resultierende Verfahren ist das sogenannte PCG-Verfahren (von engl. Preconditioned Conjugate Gradient):
Zunächst wählt man ein
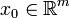 beliebig und berechnet:
beliebig und berechnet:- r0 = b − Ax0
- h0 = Cr0
- d0 = h0
Für k = 0,1,... setzt man:
Finde von xk in Richtung dk das Minimum xk + 1 und aktualisiere Gradienten und vorkonditionierten Gradienten
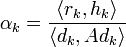
- xk + 1 = xk + αkdk
- rk + 1 = rk − αkAdk (Residuum)
- hk + 1 = Crk + 1
Korrigiere die Suchrichtung dk + 1
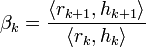
- dk + 1 = hk + 1 + βkdk
bis das Residuum in der Norm kleiner als eine Toleranz ist (
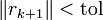 ).
).Ein häufiger Vorkonditionierer im Zusammenhang mit CG ist die unvollständige Cholesky-Zerlegung. Diese Kombination wird auch als ICCG bezeichnet und wurde in den 1970ern von Meijerink und van der Vorst eingeführt.
Zwei weitere für das PCG-Verfahren zulässige Vorkonditionierer sind der Jacobi-Vorkonditionierer C = D − 1, wobei D die Hauptdiagonale von A ist, und der SSOR-Vorkonditionierer
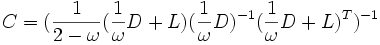 mit
mit  , wobei D die Hauptdiagonale und L die strikte untere Dreiecksmatrix von A ist.
, wobei D die Hauptdiagonale und L die strikte untere Dreiecksmatrix von A ist.Konvergenzrate des CG-Verfahrens
Man kann zeigen, dass die Konvergenzgeschwindigkeit des CG-Algorithmus durch
beschrieben wird. Hierbei ist κ(A) die Kondition der Matrix A, sowie
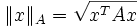 die Energienorm von A.
die Energienorm von A. 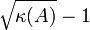 ist nicht negativ, da A symmetrisch und positiv definit ist. Ferner ist deswegen die Kondition
ist nicht negativ, da A symmetrisch und positiv definit ist. Ferner ist deswegen die KonditionAus der Minimierungseigenschaft lässt sich ferner herleiten, dass
wobei pk(z) ein beliebiges Polynom vom Grad 1 ist mit pk(0) = 1 und x * die Lösung. Mit σ(A) ist das Spektrum, also die Menge der Eigenwerte der Matrix A gemeint. Daraus folgt, dass CG ein System zu einer Matrix mit nur k Eigenwerten in k Schritten löst und dass CG für Systeme, bei denen die Eigenwerte in kleinen Umgebungen konzentriert sind, sehr schnell konvergiert. Dies wiederum liefert einen Anhaltspunkt für sinnvolle Vorkonditionierer: Ein Vorkonditionierer ist dann gut, wenn er dafür sorgt, dass die Eigenwerte konzentriert werden.
Erweiterung auf unsymmetrische Matrizen
Ist die Systemmatrix A unsymmetrisch, aber regulär, so kann das CG-Verfahren auf die Normalgleichungen
- ATAx = ATb
angewendet werden, da ATA für eine reguläre Matrix A symmetrisch und positiv definit ist. Dieses Verfahren nennt sich auch CGNR, da bei diesem Vorgehen die Norm des Residuums von b − Ax minimiert wird. Alternativ gibt es das Verfahren CGNE, welches
- AATy = b
löst mit x = ATy. Hierbei wird der Fehler (Error) minimiert.
Beide Verfahren haben den Nachteil, dass zum Einen AT zur Verfügung stehen muss, was nicht immer gegeben ist und zum Anderen die Kondition von A bei diesem Ansatz quadriert wird, was zur Verlangsamung der Konvergenz führen kann.
Literatur
- C. T. Kelley: Iterative Methods for Linear and Nonlinear Equations, SIAM, ISBN 0-89871-352-8
- P. Knabner, L. Angermann: Numerik partieller Differentialgleichungen, Springer, ISBN 3-540-66231-6
- A. Meister: Numerik linearer Gleichungssysteme, Vieweg 1999, ISBN 3-528-03135-2
- William H., Teukolsky, Saul A.:Numerical Recipes in C++, Cambridge University Press 2002, ISBN 0-521-75033-4.
- www.cs.cmu.edu An Introduction to the Conjugate Gradient Method Without the Agonizing Pain (PDF)
Wikimedia Foundation.