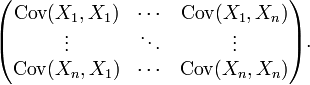Varianz-Kovarianzmatrix

Als Kovarianzmatrix (selten auch: Varianz-Kovarianz-Matrix) wird in der Wahrscheinlichkeitstheorie die Matrix aller paarweisen Kovarianzen der Elemente eines Zufallsvektors bezeichnet. Insofern verallgemeinert dieser Begriff den der Varianz einer eindimensionalen Zufallsvariable auf eine mehrdimensionale Zufallsvariable.

Die Kovarianzmatrix enthält Informationen über die Streuung eines Zufallsvektors und über Korrelationen zwischen dessen Komponenten. Ist 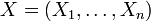$X=(X_1,\ldots,X_n)$ ein Zufallsvektor, so ist die zugehörige Kovarianzmatrix 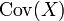$\operatorname{Cov}(X)$ gegeben durch

$\operatorname{Cov}(X) = (\operatorname{Cov}(X_i, X_j))_{i,j=1,\ldots,n}\in\R^{n,n}$.

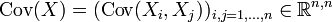Dabei bezeichnet 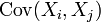$\operatorname{Cov}(X_i, X_j)$ die Kovarianz der reellen Zufallsvariablen X_i und X_j. Gelegentlich wird die Kovarianzmatrix von X auch durch Σ_X bezeichnet.

Oder ohne Matrixschreibweise: Sind 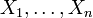$X_1,\ldots ,X_n$ Zufallsvariablen, dann ist die Kovarianzmatrix des Zufallsvektors 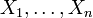$X_1,\ldots ,X_n$ gegeben durch

$\begin{pmatrix} \operatorname{Cov}(X_1,X_1) & \cdots & \operatorname{Cov}(X_1,X_n) \\ \vdots & \ddots & \vdots \\ \operatorname{Cov}(X_n,X_1) & \cdots& \operatorname{Cov}(X_n,X_n) \end{pmatrix}.$

Eigenschaften

• Die Kovarianzmatrix enthält auf der Hauptdiagonalen die Varianzen der einzelnen Komponenten des Zufallsvektors. Somit sind alle Elemente auf der Hauptdiagonalen nicht-negativ.
• Eine reelle Kovarianzmatrix ist immer symmetrisch, da die Kovarianz zweier Zufallsvariablen symmetrisch ist.
• Die Kovarianzmatrix ist stets positiv semidefinit: Wegen der Symmetrie ist jede Kovarianzmatrix mittels Hauptachsentransformation diagonalisierbar, wobei die Diagonalmatrix wieder eine Kovarianzmatrix ist. Da auf der Diagonale nur Varianzen stehen, ist die Diagonalmatrix folglich positiv semidefinit und somit auch die ursprüngliche Kovarianzmatrix.
• Umgekehrt kann jede symmetrische positiv semidefinite 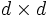$d\times d$-Matrix als Kovarianzmatrix eines d-dimensionalen Zufallsvektors aufgefasst werden.
• Aufgrund der Diagonalisierbarkeit, wobei die Eigenwerte (auf der Diagonale) wegen der positiven Semidefinitheit nicht-negativ sind, können Kovarianzmatrizen als Ellipsoide dargestellt werden.
• Für alle Matrizen 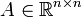$A\in\R^{n\times n}$ gilt $\operatorname{Cov}(AX) = A\,\operatorname{Cov}(X)A^T$.
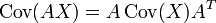• Für alle Vektoren 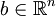$b\in\R^n$ gilt $\operatorname{Cov}(X+b) = \operatorname{Cov}(X)$.
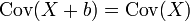• Sind X und Y unkorrelierte Zufallsvektoren, dann gilt $\operatorname{Cov}(X+Y) = \operatorname{Cov}(X)+\operatorname{Cov}(Y)$.

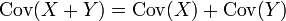Siehe auch

• Multivariate Verteilung
• Korrelationskoeffizient