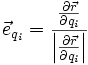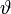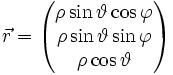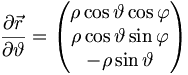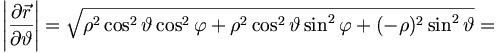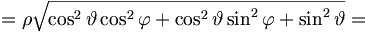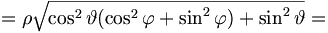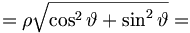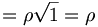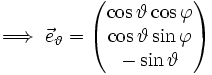Verallgemeinerte Koordinate
- Verallgemeinerte Koordinate
-
Die generalisierten Koordinaten sind ein Begriff aus der theoretischen Physik im Zusammenhang mit dem Hamilton- und dem Lagrange-Formalismus. Sie dienen der Beschreibung verallgemeinerter Bewegungsgleichungen. Sie sind meist ein reduzierter Satz von Koordinaten (Im Vergleich zu z. B. Kartesischen Koordinaten benötigt man beim Mathematischen Pendel nur die Angabe des Auslenkwinkels  und die Seillänge l.), beschreiben aber den aktuellen Systemzustand vollständig.
und die Seillänge l.), beschreiben aber den aktuellen Systemzustand vollständig.
Ausnutzung von Symmetrien
Generalisierte Koordinaten sind insbesondere bei der Beschreibung von Bewegungen hilfreich, die eine besondere Symmetrie aufweisen oder/und Zwangsbedingungen unterliegen. Geeignete generalisierte Koordinaten können den Aufwand zur Problemlösung immens reduzieren. Als anschauliches Beispiel sei die Bewegung eines Punktes auf einer Kugeloberfläche als Zwangsbedingung genannt: hier eignen sich zur Beschreibung räumliche Kugelkoordinaten 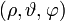 (s.u.) wesentlich besser als kartesische Koordinaten
(s.u.) wesentlich besser als kartesische Koordinaten 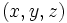 :
:
- Die Koordinate ρ ist konstant
- Die verbleibenden beiden Koordinaten
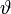 und
und  sind unabhängig voneinander
sind unabhängig voneinander
Das Polarkoordinatensystem erlaubt also eine elegantere Darstellung durch nur zwei voneinander unabhängige Koordinaten.
Beispiele
kartesische Koordinaten
So hat man im 3D-Raum zunächst einmal die normalen kartesischen Koordinaten: 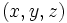
mit Richtungsvektor: 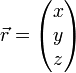
Polar-, Zylinder- und Kugelkoordinaten
Durch Einführen eines Abstandes ρ zum Nullpunkt und eines Winkels  zur x-Achse erhält man für z = 0 Polarkoordinaten
zur x-Achse erhält man für z = 0 Polarkoordinaten
mit Richtungsvektor: 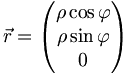
und für 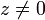 Zylinderkoordinaten
Zylinderkoordinaten
mit Richtungsvektor: 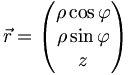
Führt man hingegen zusätzlich zu  einen zweiten Winkel
einen zweiten Winkel 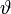 zur z-Achse ein, so erhält man Kugelkoordinaten mit Richtungsvektor:
zur z-Achse ein, so erhält man Kugelkoordinaten mit Richtungsvektor: 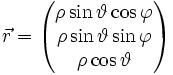
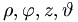 entsprechen dabei den generalisierten Koordinaten und könnten stattdessen genauso gut mit
entsprechen dabei den generalisierten Koordinaten und könnten stattdessen genauso gut mit 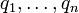 bezeichnet werden, wie es in Lehrbüchern zur theoretischen Mechanik gebräuchlich ist.
bezeichnet werden, wie es in Lehrbüchern zur theoretischen Mechanik gebräuchlich ist.
Einheitsvektoren
Es kann manchmal hilfreich sein, Einheitsvektoren in generalisierten Koordinaten zu finden. Hier gilt allgemein:
Einheitsvektor: 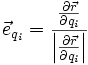
Beispiel: Finde Einheitsvektor in Kugelkoordinaten in Richtung 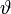
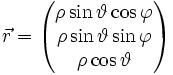
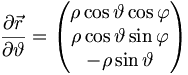
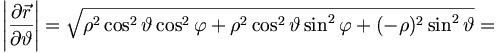
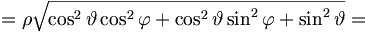
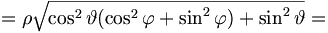
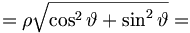
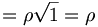
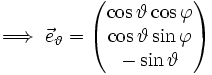
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Freiheitsgrad — Der Freiheitsgrad bezeichnet einen Parameter eines Systems. Die Eigenschaft, ein Freiheitsgrad zu sein, ergibt sich für einen Parameter daraus, Teil einer Menge von Parametern zu sein, die das System beschreiben. Das System muss dabei folgende… … Deutsch Wikipedia
обобщенная координата механизма — Каждая из независимых между собой координат, определяющих положение всех звеньев механизма относительно стойки. [Сборник рекомендуемых терминов. Выпуск 99. Теория механизмов и машин. Академия наук СССР. Комитет научно технической терминологии.… … Справочник технического переводчика
Koordinaten — Ko|ordinaten [zu kon... und lateinisch ordinare »ordnen«, also eigentlich etwa »einander Zugeordnete«], Singular Ko|ordinate die, , 1) Astronomie: astronomische Koordinaten. 2) Geographie: geographische Koordinaten. 3) … Universal-Lexikon
Differentialgeometrie — Die Differentialgeometrie stellt als Teilgebiet der Mathematik die Synthese von Analysis und Geometrie dar. Inhaltsverzeichnis 1 Historische Entwicklung und aktuelle Anwendungsgebiete 2 Teilgebiete 2.1 Elementare Differentialgeometrie … Deutsch Wikipedia
Differenzialgeometrie — Die Differentialgeometrie stellt als Teilgebiet der Mathematik die Synthese von Analysis und Geometrie dar. Inhaltsverzeichnis 1 Historische Entwicklung und aktuelle Anwendungsgebiete 2 Teilgebiete 2.1 Elementare Differentialgeometrie … Deutsch Wikipedia
Besselsche Elemente — Umrisse des Kern und Halbschattens (grün) auf der Erdoberfläche und in der Fundamentalebene (rot) während einer totalen Sonnenfinsternis Die Besselschen Elemente sind tabellarisch dargestellte Größen, die bei gegenseitiger Bedeckung von zwei… … Deutsch Wikipedia
Integralrechnung — Anschauliche Darstellung des Integrals als Flächeninhalt S unter einer Kurve der Funktion f im Integrationsbereich von a bis b. Die Integralrechnung ist neben der Differentialrechnung der wichtigste Zweig der … Deutsch Wikipedia
Gauss-Verteilung — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Gaussfunktion — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Gausskurve — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
 und die Seillänge l.), beschreiben aber den aktuellen Systemzustand vollständig.
und die Seillänge l.), beschreiben aber den aktuellen Systemzustand vollständig.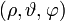 (s.u.) wesentlich besser als kartesische Koordinaten
(s.u.) wesentlich besser als kartesische Koordinaten 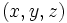 :
: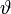 und
und  sind unabhängig voneinander
sind unabhängig voneinander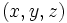
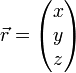
 zur x-Achse erhält man für z = 0 Polarkoordinaten
zur x-Achse erhält man für z = 0 Polarkoordinaten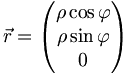
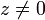 Zylinderkoordinaten
Zylinderkoordinaten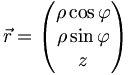
 einen zweiten Winkel
einen zweiten Winkel 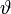 zur z-Achse ein, so erhält man Kugelkoordinaten mit Richtungsvektor:
zur z-Achse ein, so erhält man Kugelkoordinaten mit Richtungsvektor: 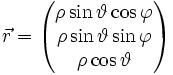
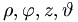 entsprechen dabei den generalisierten Koordinaten und könnten stattdessen genauso gut mit
entsprechen dabei den generalisierten Koordinaten und könnten stattdessen genauso gut mit 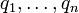 bezeichnet werden, wie es in Lehrbüchern zur theoretischen Mechanik gebräuchlich ist.
bezeichnet werden, wie es in Lehrbüchern zur theoretischen Mechanik gebräuchlich ist.