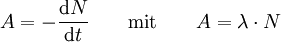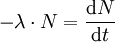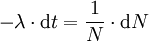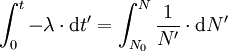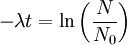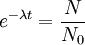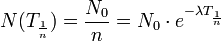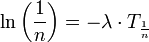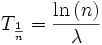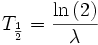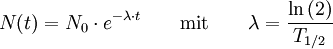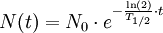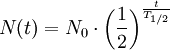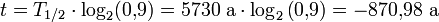Verdoppelungszeit

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Halbwertszeit (Abkürzung HWZ) ist grundsätzlich die Zeit, in der sich ein exponentiell mit der Zeit abnehmender Wert halbiert hat. Bei exponentiellem Wachstum spricht man entsprechend von einer Verdoppelungszeit.

Im engeren Sinne wird der Begriff benutzt, um die Zerfallsgeschwindigkeit von Radionukliden zu bemessen.

Ein exponentielles Verhalten liegt dann vor, wenn die Änderung mit der Zeit t einer Menge N proportional zur Menge selbst ist, wie bei Radionukliden (Mengenabnahme) oder bei vielen biologischen Wachstumsvorgängen (Mengenzunahme). Die Proportionalitätskonstante T_1/2 ist die HWZ:

(1) N(t) = N(t₀) * 2 ^-t/'T_1/2

Zur Anschauung

Die nach einer Halbwertszeit verbliebene Menge einer Substanz halbiert sich im Lauf der nächsten Halbwertszeit, d. h. es verbleibt ¹/₂·¹/₂=¹/₄; nach 3 Halbwertszeiten ¹/₈, dann ¹/₁₆, ¹/₃₂, ¹/₆₄ und so fort. Das gilt allerdings nur als statistischer Mittelwert, also dann, wenn die betrachtete Probe eine große Zahl von Molekülen oder Atomen enthält. Die Umwandlung z. B. eines einzelnen Atomkerns kann nicht vorhergesagt werden, sondern es kann lediglich eine Wahrscheinlichkeit für diese Umwandlung innerhalb einer gegebenen Zeit angegeben werden (Zerfallswahrscheinlichkeit λ, siehe unten). Die Wahrscheinlichkeit, dass ein betrachteter Kern sich innerhalb der ersten Halbwertszeit umwandelt, beträgt 50 %, dass er sich innerhalb von 2 Halbwertszeiten umwandelt, 50 % + 25 % = 75 %, bei 3 Halbwertszeiten beträgt der Wert 50 % + 25 % + 12,5 % = 87,5 %, usw.

Zerfallsgesetz

Es sei ein radioaktives Präparat mit N₀ Kernen und der Aktivität A. Dann gilt für die Anzahl dN der in der Zeit dt zerfallenen Kerne:

$A = - \frac{\mathrm d N}{\mathrm d t} \qquad \text{mit} \qquad A = \lambda \cdot N$

$-\lambda \cdot N = \frac{\mathrm d N}{\mathrm d t}$

$-\lambda \cdot \mathrm d t=\frac{1}{N} \cdot \mathrm d N$

$\int_0^t -\lambda \cdot \mathrm dt'=\int_{N_0}^N\frac{1}{N'} \cdot \mathrm dN'$

$-\lambda t =\ln\left(\frac{N}{N_0}\right)$

$e^{-\lambda t} = \frac{N}{N_0}$

(2) $N(t)= N_0 \cdot e^{-\lambda t}$

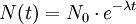
Nach der Zeit t sind also von N₀ Ausgangskernen noch N(t) übrig.

Hierbei ist die Geschwindigkeit der Abnahme durch die Zerfallskonstante λ (Lambda) bestimmt. Sie ist das Reziproke der mittleren Lebensdauer τ = 1 / λ, also der Zeit, nach der die Zahl der Atome sich um den Faktor e verringert hat. τ unterscheidet sich von der Halbwertszeit T_1/2 nur um den konstanten Faktor ln(2):

(3) T_1/2 = τ ln(2) ≈ 0,693 τ.

Ersetzt man im Zerfallsgesetz (2) τ durch T_1/2, folgt die unter (1) angegebene Schreibweise:

(1) N(t) = N(t₀) * 2 ^-t/'T_1/2

Mathematische Definition der Halbwertszeit

Sei 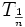$T_{\frac{1}{n}}$ die Zeit, nach der die Ausgangsmenge N₀ auf das 1/n-fache abgefallen ist (für die Halbwertszeit gilt n=2):

$N(T_{\frac{1}{n}})= \frac{N_0}{n} = N_0 \cdot e^{-\lambda T_{\frac{1}{n}}}$

Danach wird auf beiden Seiten durch N₀ geteilt und logarithmiert.

$\ln\left(\frac{1}{n}\right)= -\lambda \cdot T_{\frac{1}{n}}$

Daraus folgt dann unter Beachtung der Logarithmengesetze:

$T_{\frac{1}{n}} = \frac{\ln\left(n\right)}{\lambda}$

Speziell für die Halbwertszeit gilt (n=2):

$T_{\frac{1}{2}} = \frac{\ln\left(2\right)}{\lambda}$

Daraus ergibt sich für das Zerfallsgesetz:

$N(t)= N_0 \cdot e^{-\lambda \cdot t} \qquad \text{mit} \qquad \lambda = \frac{\ln\left(2\right)}{T_{1/2}}$

$N(t)= N_0 \cdot e^{- \frac{\ln\left(2\right)}{T_{1/2}}\cdot t}$

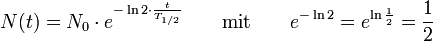$N(t)= N_0 \cdot e^{-\ln 2 \cdot \frac{t}{T_{1/2}}} \qquad \text{mit} \qquad e^{-\ln 2} = e^{\ln \frac{1}{2}} = \frac{1}{2}$ (Exponentialgesetze)

$N(t)= N_0 \cdot \left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}}$

Diese Formulierung des Zerfallsgesetzes veranschaulicht am besten, dass sich nach der Halbwertszeit T_{1 / 2} die Anzahl der noch nicht zerfallenen Kerne halbiert hat.

Beispiele

Radioaktive Halbwertszeit

Die Halbwertszeit ist in der Kernphysik diejenige Zeitspanne, in der die Menge eines bestimmten radioaktiven Nuklids auf die Hälfte gesunken ist, das heißt sich in andere Atome umgewandelt hat. Für jedes Nuklid ist die Halbwertszeit eine Konstante.

Die Anzahl der verbleibenden Kerne zu einer bestimmten Zeit ist durch das Zerfallsgesetz (siehe oben) gegeben.

Halbwertszeiten einiger radioaktiver Nuklide:

Element	Formelzeichen	Halbwertszeit
Tellur	128Te	ca. 7·1024 Jahre (7 Quadrillionen Jahre)
Selen	82Se	ca. 1,08·1020 Jahre (108 Trillionen Jahre)
Bismut	209Bi	ca. 1,9·1019 Jahre (19 Trillionen Jahre)
Thorium	232Th	14,05 Mrd. Jahre
Uran	238U	4,468 Mrd. Jahre
Uran	235U	704 Mio. Jahre
Iod	129I	15,7 Mio. Jahre
Neptunium	237Np	2,144 Mio. Jahre
Technetium	99Tn	211.100 Jahre
Plutonium	239Pu	24.110 Jahre
Kohlenstoff	14C	5.730 Jahre
Radium	226Ra	1.602 Jahre
Americium	241Am	432,2 Jahre
Plutonium	238Pu	87,74 Jahre
Caesium	137Cs	30,2 Jahre
Strontium	90Sr	28,64 Jahre
Tritium	3H	12,32 Jahre
Cobalt	60Co	5,3 Jahre
Schwefel	35S	87,5 Tage
Iod	131I	8,02 Tage
Radon	222Rn	3,8 Tage
Francium	223Fr	22 Minuten
Thorium	223Th	0,6 Sekunden
Polonium	212Po	0,3 µs
Beryllium	8Be	6,7 · 10-17 s (0,67 Trillionstelsekunden)

Rein mathematisch betrachtet verschwindet die radioaktive Substanz also nie, physikalisch ist natürlich mit der Umwandlung des letzten Atoms eine Grenze gesetzt (die Substanz komplett verschwunden). Oft nutzt man als Abschätzung für die Zeitdauer bis zur Bedeutungslosigkeit einer radioaktiven Strahlung die zehnfache Halbwertszeit, was einer Abnahme auf das 2^-10-fache (= 1/1024) entspricht.

Beim praktisch wichtigen Problem der Aufnahme radioaktiver Stoffe in den Körper spielt nicht nur die Halbwertszeit im physikalischen Sinn, sondern auch die Wiederausscheidung des Stoffes durch den biologischen Stoffwechsel eine Rolle. Auch diese kann in manchen Fällen nach einem Exponentialgesetz erfolgen, also durch eine Halbwertszeit beschrieben werden. In diesen Fällen muss zwischen der physikalischen und der biologischen Halbwertszeit unterschieden werden (siehe unten).

Siehe auch: Lebensdauer (Physik)

Radiokohlenstoffmethode

Siehe auch Radiokohlenstoffdatierung

Das radioaktive Kohlenstoffnuklid ¹⁴C ist in einem festen Verhältnis im Kohlenstoffdioxid unserer Atmosphäre enthalten. Durch den anteiligen Einbau des Nuklids bei der Photosynthese in die Biomasse der Pflanzen und weiter über die Nahrungskette kommt es auch im Körper aller Lebewesen zu einem näherungsweise festen Verhältnis zwischen stabilem ¹²C und radioaktivem ¹⁴C. Wenn ein Lebewesen stirbt, dann beendet es die Photosynthese bzw. die Nahrungsaufnahme. Das hat zur Folge, dass der Anteil an ¹⁴C ab genau diesem Zeitpunkt entsprechend dem radioaktiven Zerfall exponentiell mit einer Halbwertszeit von 5730 Jahren abnimmt. Durch Messung der ionisierenden Reststrahlung, die von einem abgestorbenen Organismus ausgesendet wird, kann der Zeitpunkt des Todes des Lebewesens abgeschätzt werden. Dazu wird die Zeit ermittelt, die benötigt wird um über das Zerfallsgesetz von dem natürlichen ¹²C/¹⁴C-Verhältnis zum gemessenen ¹²C/¹⁴C-Verhältnis zu gelangen. Die so ermittelte Zeitspanne entspricht dem Alter des Fundes.

Anwendungsbeispiel

Der Balken eines historischen Gebäudes hat noch 90 % des ursprünglichen Gleichgewichtsanteils an ¹⁴C in frischer Pflanzenmasse. Dann gilt für die verstrichene Zerfallszeit:

$t = T_{1/2} \cdot \log_2(0{,}9) = 5730\ \mathrm{a} \cdot \log_2\left(0{,}9\right) = -870{,}98\ \mathrm{a}$

Das bedeutet, dass der Baum, aus dem der Balken gemacht wurde, vor etwa 871 Jahren geschlagen worden ist.

Die Datierung ist nicht auf das Jahr genau. Die mögliche Genauigkeit hängt von der Menge verfügbaren Probematerials, der aufgewendeten Zähldauer und der Kalibrierung für den entsprechenden Zeitraum ab. Für die Messung mittels Beschleunigermassenspektrometrie genügen wesentlich kleinere Mengen des Probenmaterials. Zudem werden in neuerer Zeit Untersuchungen komplizierter, da der C-14-Anteil durch oberirdische Atomwaffenversuche kurzfristig gesteigert wurde. Andererseits steigt auch der C-12-Anteil durch die massenhafte Verbrennung fossiler Energieträger, wodurch die Datierung von Funden besonders in der Nähe von Autobahnen erschwert wird.

Für Feinheiten siehe den Hauptartikel: Radiokohlenstoffdatierung

Biologische Halbwertszeit

Die biologische Halbwertszeit auch Eliminationshalbwertszeit genannt, bezeichnet im speziellen die Zeitspanne t_1/2, in welcher in einem biologischen Organismus (Mensch, Tier, Pflanze, Einzeller) der Gehalt einer inkorporierten radioaktiven, toxischen oder pharmazeutischen Substanz durch die Wirkung aller beteiligten biologischen und physikalischen Prozesse (Stoffwechsel, Ausscheidung, radioaktiver Zerfall, etc.) auf die Hälfte abgesunken ist.

In der Pharmakokinetik bezeichnet man als Halbwertszeit die Zeit, in der die Hälfte des aufgenommenen Arzneimittels verstoffwechselt und/oder ausgeschieden ist. Da sich die biologische Halbwertszeit aus verschiedenen Prozessen zusammensetzt, die teilweise unterschiedliche Konzentrationsabhängigkeiten besitzen, ist sie nicht immer unabhängig von der Ausgangskonzentration des untersuchten Stoffes (vgl. Plasmahalbwertszeit).

Siehe auch: Kontextsensitive Halbwertszeit

Effektive Halbwertszeit

Die Effektive Halbwertszeit berücksichtigt sowohl die physikalische als auch die biologische Halbwertszeit.

Bibliometrische Halbwertszeiten

In der Bibliometrie lassen sich bei der Untersuchung von Publikationen verschiedene Halbwertszeiten feststellen. Brooks untersuchte als einer der ersten Halbwertszeiten auf diesem Gebiet.

Die Halbwertszeit von Literatur beträgt etwa 5 Jahre. Dies gilt sowohl für die Lektüre als auch die Anzahl der Zitationen. Das heißt, dass ein Werk durchschnittlich jedes Jahr um etwa 14 % weniger oft aus einer Bibliothek entliehen oder zitiert wird als im vorangegangenen (abgesehen von Klassikern und den neuesten Werken).

Die Halbwertszeit von Hyperlinks im WWW beträgt etwa 51 Monate. Das heißt, dass nach einem Jahr etwa 15 % aller Hyperlinks nicht mehr gültig sind.

Halbwertszeiten von PKW (bzgl. Preis)

Der Wiederverkaufswert eines PKW sinkt annähernd exponentiell mit seinem Alter, bei einer Halbwertszeit von ca. 4–5 Jahren. Beispielsweise liegt der Preis eines Neuwagens des Modells VW-Beetle heute (2006) bei etwa 20.000 €, das Modell aus dem Jahr 2002 kostet etwa 10.000 € und das von 1998 etwa 5.000 €.

Verwandte Begriffe

Halbwertsdicke, Zehntelwertszeit, Zehntelwertsdicke