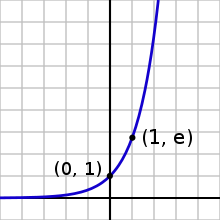
Exponentielles Wachstum

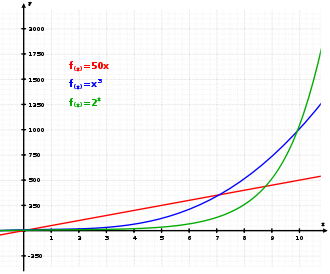Das Diagramm zeigt, wie exponentielles Wachstum (grün) sowohl lineares (rot) als auch kubisches (blau) Wachstum übertrifft.

• Lineares Wachstum: f_(x) = 50x
• Kubisches Wachstum: f_(x) = x³
• Exponentielles Wachstum: f_(x) = 2^x

exp(x)

Verändert sich ein Bestand pro Zeiteinheit um einen festen Prozentsatz des sich damit stets ändernden Zeitwertes, bezeichnen wir diesen Vorgang als exponentiell, gleichermaßen bei der Zunahme (dem Wachstum) oder der Abnahme (auch Zerfall oder negatives Wachstum genannt). Den genannten festen Prozentsatz bezeichnen wir als Wachstumsrate. Mathematisch wird dieser exponentielle Prozess durch eine Exponentialfunktion beschrieben. Verändert sich hingegen ein Bestand pro Zeiteinheit um einen sich nicht ändernden Betrag, bezeichnen wir dies als lineares Wachstum.

Eigenschaften

Zeitlich exponentielle Vorgänge

Zeitlich exponentielle Vorgänge lassen sich durch die Formeln

$N_t = N_0 \cdot e^{\lambda t}$ für exponentielles Wachstum und

$N_t = N_0 \cdot e^{- \lambda t}$ für exponentielle Abnahme beschreiben.

Dabei ist N₀ der Wert zum Ausgangszeitpunkt (t = 0), N_t der Wert zum Zeitpunkt t und e die Eulersche Zahl.

Charakteristisch für jeden exponentiellen Vorgang ist die im Exponenten auftretende Wachstumskonstante (Wachstum) oder Zerfallskonstante (Abnahme) λ. Wenn für exponentielle Vorgänge einheitlich die Formel für exponentielles Wachstum verwendet wird, so ist λ bei einer Abnahme negativ; üblicher ist es aber, λ auch bei Abnahmevorgängen positiv zu definieren und in der Gleichung wie oben das Minuszeichen vor den Exponenten zu setzen.

Die Verdoppelungszeit T (Wachstum) beziehungsweise Halbwertszeit (Abnahme) hängt dann folgendermaßen direkt mit der Größe λ zusammen:

$\lambda \cdot T = \ln 2$

Dabei ist ln  der natürliche Logarithmus.

Funktionswerte, die im Abstand fester Zeitschritte Δt aufeinander folgen, bilden eine geometrische Folge mit dem Faktor q = e^λ. Geometrische Folgen stellen eine Möglichkeit dar, exponentielle Vorgänge in elementarer Weise zu beschreiben.

Exponentielles Verhalten ist in der Natur ein oft beobachteter Vorgang. Der mathematische Hintergrund dafür ist, dass die obige Formel die gewöhnliche Differentialgleichung

y'(t) = λy(t)

erfüllt. Diese Gleichung besagt, dass die Änderung eines Wertes zu jeder Zeit proportional zu diesem Wert ist. Im Falle einer Bakterienkultur bedeutet dies beispielsweise, dass umso mehr Bakterien (durch Zellteilung) pro Zeiteinheit neu gebildet werden, je mehr Bakterien bereits vorhanden sind.

Natürliches Wachstum und Sättigung

Viele natürliche Wachstumsprozesse lassen sich in ihrem Anfangsstadium (unter Idealbedingungen auch länger) sehr gut durch eine Exponentialfunktion beschreiben. So wachsen Bakterienkolonien und viele Populationen von Lebewesen ohne natürliche Feinde zu Beginn exponentiell. Die Zeit der Verdopplung wird hierbei als Generationszeit bezeichnet. Früher oder später tritt jedoch fast immer eine Sättigung auf (in biologischen Zusammenhängen fast immer durch die Konkurrenz der Individuen um Nahrung oder Platz), so dass Prognosen, die auf Extrapolation exponentieller Wachstumskurven beruhen, zu Überschätzungen führen, wenn dies nicht mit einbezogen wird. Eine realistischere Beschreibung natürlicher Wachstumsvorgänge, die auch Sättigungseffekte berücksichtigt, ist mittels der logistischen Funktion und der logistischen Gleichung möglich. Auch bei Pyramidenspielen und Schenkkreisen spielen solche Sättigungseffekte eine wichtige Rolle.

Schrittweise-exponentielles Wachstum

Neben kontinuierlichen exponentiellen Vorgänge werden manchmal auch schrittweise verwendet. Bei der Berechnung des Zinseszins ist es beispielsweise bis heute üblich, schrittweise vorzugehen, also den Ertrag nicht sofort zu verzinsen, sondern erst ab einem bestimmten Termin (z. B. dem Jahresende). Die Formel hierfür ist dann

$N_t = N_0 \cdot (1+p)^t,$

wobei p der Zinssatz bzw. die schrittweise Wachstumsrate ist.

Für ganze Vielfache der Schrittweite lässt sich ein äquivalenter kontinuierlicher exponentieller Vorgang angeben. Für diesen gilt

$\lambda=\ln(1+p).\,$

5 % jährliche Zinsen entsprechen damit beispielsweise einer kontinuierlichen Wachstumsrate von etwa 4,88 Prozent pro Jahr (siehe dazu auch Zinssatz).

Faustformel für Verdoppelungszeit

Um die Verdoppelungszeit T einer exponentiell wachsenden Größe zu überschlagen, kann man die Faustformel:

$T \approx \frac{70}i$

verwenden, wobei i Der Prozentsatz des Wachstums pro Zeiteinheit ist. Im Zähler steht bei dieser Faustformel 70, weil:

$100 \cdot \ln 2 \approx 69,3 \approx 70$

Örtlich exponentielle Vorgänge

Aber nicht nur zeitabhängige, sondern auch ortsabhängige Veränderungen können exponentiell verlaufen. Das Absorptionsgesetz, das für manche Arten von Strahlung beim Eintritt in eine homogene Materieschicht gilt, hat dieselbe mathematische Form wie die o.a. Gleichungen für zeitlich exponentielles Wachstum.

Beispiele

Ein verbreitetes Beispiel, welches die extremen Beträge illustriert, die durch die Annahme von über lange Zeit gleichbleibendem schrittweise exponentiellen Wachstum aufgrund von Zinseszinseffekten rechnerisch erhalten werden, ist das Beispiel des im Jahr Null angelegten Pennys, das auf dem Anwachsen von Kapital oder Schulden durch Zins und Zinseszins beruht (→Zinsrechnung).

Zunahme der Schichtdicke beim Falten

5-fach gefaltete Mylarfolie

Bei jedem Falten verdoppelt sich die Dicke von Papier oder Folie. Auf diese Weise lassen sich dünne Folien mit einem einfachen Messschieber ausmessen. Die Mylarfolie auf dem Bild besteht nach 5-fachem Falten aus 2⁵ = 32 Lagen Folie, die gemeinsam eine Dicke von 480 µm haben. Eine Folie ist also ca. 15 µm stark. Nach 10-fachem Falten wäre die Lage bereits 15 mm dick, nach weiteren 10 Faltungen mehr als 15,7 m. Da sich gleichzeitig auch die Stapelfläche exponentiell verringert, lässt sich normales Papier kaum mehr als zehn Mal zusammenschlagen.

Verdoppelungszeit eines Sparguthabens

Bei einem Sparbuch mit 5 % Zinsen p.A. ist die Verdoppelungszeit nach obenstehender Faustformel

$\frac{70}5 \approx \text{14 Jahre}$

Weitere Beispiele

• Schachbrett mit einem Weizenkorn (Weizenkornlegende)
• Bei radioaktivem Zerfall die Abnahme des ursprünglichen Nuklids
• Kernspaltung: je nach Kritikalität exponentiell ab- oder zunehmend
• Krebs (Medizin)
• Weltbevölkerung