Verschiebungsinvarianz

Stationarität bezeichnet in der Mathematik eine Eigenschaft von stochastischen Prozessen oder gewöhnlichen Differentialgleichungen. Dieser Artikel behandelt ersteres.

Definition

Zeitreihe von Residuen, nicht-stationär gemäß dem Dickey-Fuller Test

Ein stochastischer Prozess 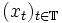$(x_t)_{t\in \mathbb{T}}$ heißt stark stationär, wenn die Verteilung von 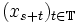$(x_{s+t})_{t\in \mathbb{T}}$ nicht vom Index 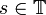$s \in \mathbb{T}$ abhängt.

Ein stochastischer Prozess 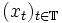$(x_t)_{t\in \mathbb{T}}$ heißt schwach stationär, wenn

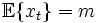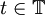
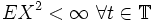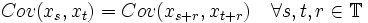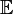1. $\mathbb{E}\{x_t\} = m$ ist konstant (gleich) für alle $t\in \mathbb{T}$
2. $EX^2 < \infty \ \forall t \in \mathbb{T}$.
3. $Cov(x_s,x_t)=Cov(x_{s+r},x_{t+r}) \quad \forall s,t,r\in \mathbb{T}$.

$\mathbb{E}$ bezeichnet hier den Erwartungswert, 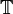$\mathbb{T}$ steht für eine beliebige Indexmenge (Teilmenge der wohlgeordneten reellen Zahlen), meist die ganzen Zahlen, manchmal auch die natürlichen Zahlen oder die reellen Zahlen, mit der oft die Zeit modelliert wird. Var bezeichnet die Varianz, Cov die Kovarianz.

Interpretation

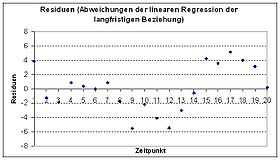
Stationarität ist eine der bedeutendsten Eigenschaften stochastischer Prozesse in der Zeitreihenanalyse. Mit der Stationarität erhält man Eigenschaften, die nicht nur für einzelne Zeitpunkte gelten, sondern Invarianzen über die Zeit hinweg sind. Die Zeitreihe hat zu allen Zeitpunkten den gleichen Erwartungswert und die gleiche Varianz. (Die wichtigste Klasse von nichtstationären Prozessen sind integrierte Prozesse.)

Mit der ersten Eigenschaft kann man zu einem neuen Prozess x_t − E[x_t] übergehen, für den dann E[x_t − E[x_t]] = 0 gilt. Dieser Prozess wird auch zentrierter Prozess genannt. Man kann also o.B.d.A. annehmen, ein stationärer stochastischer Prozess habe den Mittelwert 0.

Die zweite Eigenschaft sagt schlichtweg, dass jede der Zufallsvariable endliche Varianz hat und somit zu dem Hilbertraum L² gehört. Hieraus folgt dann auch, dass der Erwartungswert E{x_t} existiert.

Die dritte Forderung stellt eine Beziehung zwischen den unterschiedlichen Zeitpunkten her und ist damit die bedeutendste Eigenschaft. Sie sagt aus, dass die Kovarianzen zwischen den Zeitpunkten nicht von den beiden Zeitpunkten selbst, sondern nur von dem Abstand der beiden Zeitpunkte zueinander abhängt. Die Bedingung kann auch so formuliert werden, dass γ(r) eine Funktion nur einer einzigen Variablen r ist. Dies hat unter anderem zur Konsequenz, dass Γ = Exx ^* − (Ex)(Ex) ^* eine unendliche Block Toeplitz-Matrix ist.

Geometrische Bedeutung

Die geometrische Interpretation des univariaten Falles (n = 1) greift auf den Hilbertraum L² zurück, dessen Elemente die einzelnen Zufallsvariable des Prozesses sind. Die geometrische Interpretation unterstützt das tiefere Verständnis des Begriffs der Stationarität.

Da 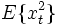$E\{x_t^2\}$ eine Norm in L² ist, kann die Forderung 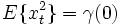$E\{x_t^2\}=\gamma(0)$ so verstanden werden, dass alle Prozessvariable gleich lang sind, d. h. auf einer Kugel liegen.

Ex_{t + s}x_t = γ(s) sagt dann, obiger Interpretation folgend, dass für festes s alle x_t den gleichen Winkel einschließen. Erhöht man s um Eins, so wird immer um denselben Winkel weitergedreht.

Forderung (ii) bedeutet nicht anderes als < x_t,1 > = m, also der Winkel zwischen der Einheit und jeder Prozessvariablen ist konstant. Hier wird ein Breitengrad aus der Einheitskugel ausgeschnitten.

Stationarisierung

Eine nichtstationäre Zeitreihe stationär zu machen ist eine wichtige erste Aufgabe bei der Zeitreihenanalyse. Weit verbreitete Methoden sind hier die Bildung von ersten Differenzen, das Umskalieren der Zeitreihe oder Logarithmieren.

Beispiele

Der wichtigste stationäre Prozess ist das weiße Rauschen. Des weiteren sind noch bestimmte Gauss-Prozesse und MA-Modelle stationär. Von theoretischer Bedeutung sind auch noch harmonische Prozesse, die unter gewissen Bedingungen stationär sind.

Literatur

• Peter J. Brockwell, Richard A. Davis: Time Series: Theory and Methods. Springer Verlag, Berlin 2002, ISBN 0387974296
• G. E. P. Box, G. M. Jenkins: Times Series Analysis: Forecasting and Control. 3. Auflage, ISBN 0130607746