Polygammafunktion

Die ersten Polygammafunktionen im Reellen
 m = 0    m = 1    m = 2    m = 3    m = 4

In der Mathematik sind die Polygamma-Funktionen eine Reihe spezieller Funktionen, die als die Ableitungen der Funktion ln Γ(x) definiert sind. Dabei bezeichnet Γ(x) die Gammafunktion und ln  den natürlichen Logarithmus.

Die ersten beiden Polygammafunktionen werden Digammafunktion und Trigammafunktion genannt.

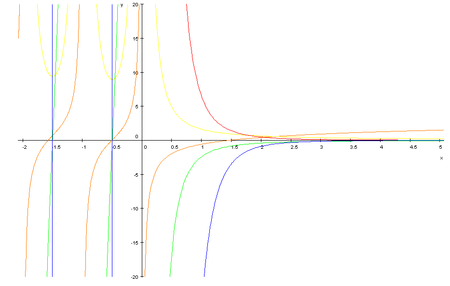
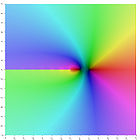
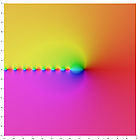
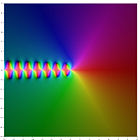
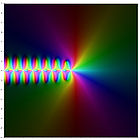
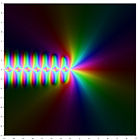
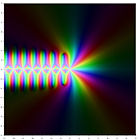
Darstellung der ersten fünf Polygammafunktionen in der komplexen Ebene

ln Γ(z)	ψ(0)(z)	ψ(1)(z)	ψ(2)(z)	ψ(3)(z)	ψ(4)(z)

Notation

Die Polygammafunktionen werden mit dem kleinen griechischen Buchstaben psi (ψ) bezeichnet. Bei der ersten Polygammafunktion, der Digammafunktion, wird der Index meist weggelassen oder als 0 festgelegt; die zweite Polygammafunktion, also die Trigammafunktion, wird dann mit ψ₁ (oder selten ψ⁽¹⁾) bezeichnet und ist die zweite Ableitung von log Γ(x). Allgemein ist die n-te Polygammafunktion oder Polygammafunktion der Ordnung n mit ψ_n oder ψ⁽ⁿ⁾ bezeichnet und als die (n + 1)-te Ableitung von log Γ(x) definiert.

Definition und weitere Darstellungen

Es ist

$\psi_n=\frac{\mathrm d^{n+1}}{\mathrm dx^{n+1}}\ln\Gamma(x)=\frac{\mathrm d^n}{\mathrm dx^n}\,\psi(x)$

mit der Digammafunktion ψ(x). Derartige Ableitungen werden auch als logarithmische Ableitungen von Γ bezeichnet.

Eine Integraldarstellung ist

$\psi_m(z)= (-1)^{m+1}\int\limits_0^\infty \frac{t^m e^{-zt}}{1-e^{-t}}\,\mathrm dt$

für Re(z) > 0 und m > 0.

Eigenschaften

Differenzengleichungen

Die Polygammafunktionen haben die Differenzengleichungen

$\psi_m(z+1)= \psi_m(z) + (-1)^m\; m!\; z^{-m-1}.$

Multiplikationsformel

Die Multiplikationsformel ist gegeben durch

$k^{m} \psi_{m-1}(kz) = \sum_{n=0}^{k-1} \psi_{m-1}\left(z+\frac{n}{k}\right)$

für m > 1 (Zum Fall m = 0, also der Digammafunktion, siehe dort.)

Reihendarstellungen

Eine Reihendarstellung der Polygammafunktion lautet

$\psi_m(z) = (-1)^{m+1}\; m!\; \sum_{k=0}^\infty \frac1{(z+k)^{m+1}}$

wobei m > 0 und $z\not= -1,-2,-3,\ldots$ eine beliebige komplexe Zahl außer den negativen ganzen Zahlen ist. Die Formel lässt sich einfacher unter Verwendung der hurwitzschen Zetafunktion ζ(x,y) schreiben als

$\psi_m(z) = (-1)^{m+1}\; m!\; \zeta (m+1,z).$

Die Verallgemeinerung der Polygammafunktionen auf beliebige, nichtganze Ordnungen m ist weiter unten angegeben.

Eine weitere Reihendarstellung ist

$\psi_n(z) = -\gamma \delta_{n,0} \; - \; \frac{(-1)^n n!}{z^{n+1}} \; + \; \sum_{k=1}^{\infty} \left(\frac{1}{k} \delta_{n,0} \; - \; \frac{(-1)^n n!}{(z+k)^{n+1}}\right),$

wobei δ_n,0 das Kronecker-Delta bezeichnet.

Skizze zur Herleitung:

Nach Oskar Schlömilch ist unter Verwendung des weierstraßschen Produktsatzes.

$\frac1{\Gamma(z)} = z \; \mbox{e}^{\gamma z} \; \prod_{n=1}^{\infty} \left(1 + \frac{z}{n}\right) \; \mbox{e}^{-z/n} \qquad | \text{ Kehrwert}$

$\Gamma(z) = \frac{\mbox{e}^{-\gamma z}}{z} \; \prod_{n=1}^{\infty} \left(1 + \frac{z}{n}\right)^{-1} \; \mbox{e}^{z/n} \qquad | \text{ Logarithmus}$

$\ln\Gamma(z) = -\gamma z - \ln(z) + \sum_{n=1}^{\infty} \left(\frac{z}{n} - \ln(1 + \tfrac{z}{n}) \right) \qquad | \;n\text{-te Ableitung}=\psi_n$

$\psi_n(z) = \frac{\mathrm d^{n+1}}{\mathrm dz^{n+1}}\ln\Gamma(z) = -\gamma\delta_{n,0} \; - \; \frac{(-1)^n n!}{z^{n+1}} \; + \; \sum_{k=1}^{\infty} \left(\frac1k \delta_{n,0} \; - \; \frac{(-1)^n n!}{(z+k)^{n+1}}\right)$

Die Taylor-Reihe um z = 1 ist gegeben durch

$\psi_m(z+1)= \sum_{k=0}^\infty (-1)^{m+k+1} (m+k)!\; \zeta (m+k+1)\; \frac {z^k}{k!},$

die für | z | < 1 konvergiert. ζ bezeichnete dabei die Riemannsche Zetafunktion.

Spezielle Werte

Die Werte der Polygammafunktionen für rationale Argumente lassen sich meist ausdrücken unter Verwendung von Konstanten und Funktionen wie π, Quadratwurzel, Clausen-Funktion Cl(x), Riemannsche ζ-Funktion, Catalansche Konstante G sowie Dirichletsche β-Funktion; z.B.

$\psi_n(\tfrac12)=(-1)^{n+1}n!(2^{n+1}-1)\zeta(n+1), \qquad n\in\N$

Allgemein gilt ferner:

$\psi_n(1)=(-1)^{n+1}n!\zeta(n+1),\qquad n\in\N$.

Die n-te Ableitung des Tangens kann ebenfalls mit der Polygammafunktion ausgedrückt werden:

$\frac{\mathrm{d}^n}{\mathrm{d}x^n}\tan x=\frac{\psi_n(\tfrac12+\tfrac{x}{\pi})-(-1)^n\,\psi_n(\tfrac12-\tfrac{x}{\pi})}{\pi^{n+1}}$.

Verallgemeinerte Polygammafunktion

Vorbemerkungen: Fraktionale Infinitesimalrechnung

Für das Verständnis dieses Abschnitts sind folgende fraktionale Ableitungsregeln für Potenzen angegeben:

$\frac{\mathrm{d}^s}{\mathrm{d}x^s}\,x^a= \begin{cases} \dfrac{\Gamma(a+1)}{\Gamma(a-s+1)}\,x^{a-s} & ;\;-(a+1)\notin\N_0 \\ \dfrac{(-1)^{a+1}}{\Gamma(-a)}\, \dfrac{\ln x-\psi(a-s+1)-\gamma}{\Gamma(a-s+1)}\,x^{a-s} & \text{sonst} \end{cases}$

für $a\ne 0$ sowie

$\frac{\mathrm{d}^s}{\mathrm{d}x^s} \left( \frac{\ln x-\psi(a+1)-\gamma}{\Gamma(a+1)}\,x^a \right) = \begin{cases} \displaystyle{ \frac{\ln x-\psi(a-s+1)-\gamma}{\Gamma(a-s+1)}\,x^{a-s} } & ;\; s-a-1\notin\N_0 \\ (-1)^{s-a-1}(s-a-1)!\,x^{a-s} & \text{sonst,} \end{cases}$

außerdem gelte die Verschiebungsinvarianz

$\frac{\mathrm{d}^s}{\mathrm{d}x^s}\,f(x+C)= \left. \frac{\mathrm{d}^s f}{\mathrm{d}t^s}(t) \right|_{t=x+C}$.

Dabei ist ψ(s) = ψ₀(s) die Digammafunktion und γ bezeichnet die Euler-Mascheroni-Konstante.

Definition und Eigenschaften

Nun betrachtet man die fraktionale Ableitung

$\psi_s(z)=\frac{\mathrm{d}^{s+1}}{\mathrm{d}z^{s+1}}\ln\Gamma(z)$

vom komplexen Grad s und gelangt durch die Beziehung $\scriptstyle\Gamma(z+1)=z\,\Gamma(z)$ und die Identität $\scriptstyle\ln z=z^0\left(\ln z-\psi(1)-\gamma\right)/\Gamma(1)$ zu der Funktionalgleichung

$\psi_s(z+1)=\psi_s(z)+\frac{\ln z-\psi(-s)-\gamma}{\Gamma(-s)}\,z^{-(s+1)}$.

Unter Zuhilfenahme der Hurwitzschen ζ-Funktion erhält man dann für $\scriptstyle z\in\C$ die Gleichung

$\psi_s(z)=\frac1{\Gamma(-s)}\left(\frac{\partial}{\partial s}+\psi(-s)+\gamma\right)\zeta(s+1,z)$,

welche die Funktionalgleichung erfüllt.^[1] Nutzt man die erste Differentiationsregel aus den Vorbemerkungen aus und vergleicht die Partialbruchzerlegung des Kotangens mit der Definition der Hurwitzschen ζ-Funktion, erhält man die Spiegelgleichung

$\mathrm{e}^{i\pi s}\,\psi_s(1-z)-\psi_s(z)=\pi\frac{\mathrm{d}^s}{\mathrm{d}z^s}\cot(\pi z)$.

q-Polygammafunktion

Die q-Polygammafunktion ist definiert durch^[2]

$\psi_n\,^q(z)=\frac{\partial^n\psi_q(z)}{\partial z^n}$.

Referenzen

1. ↑ Oliver Espinosa and Victor H. Moll: A Generalized Polygamma Function auf arXiv.org e-Print archive 2003.
2. ↑ Eric W. Weisstein: q-Polygamma Function. In: MathWorld. (englisch)

• Milton Abramowitz und Irene Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 978-0-486-61272-0. Siehe §6.4
• Eric W. Weisstein: Polygamma Function auf MathWorld, in functions.wolfram.com, in references.worlfram.com.